About

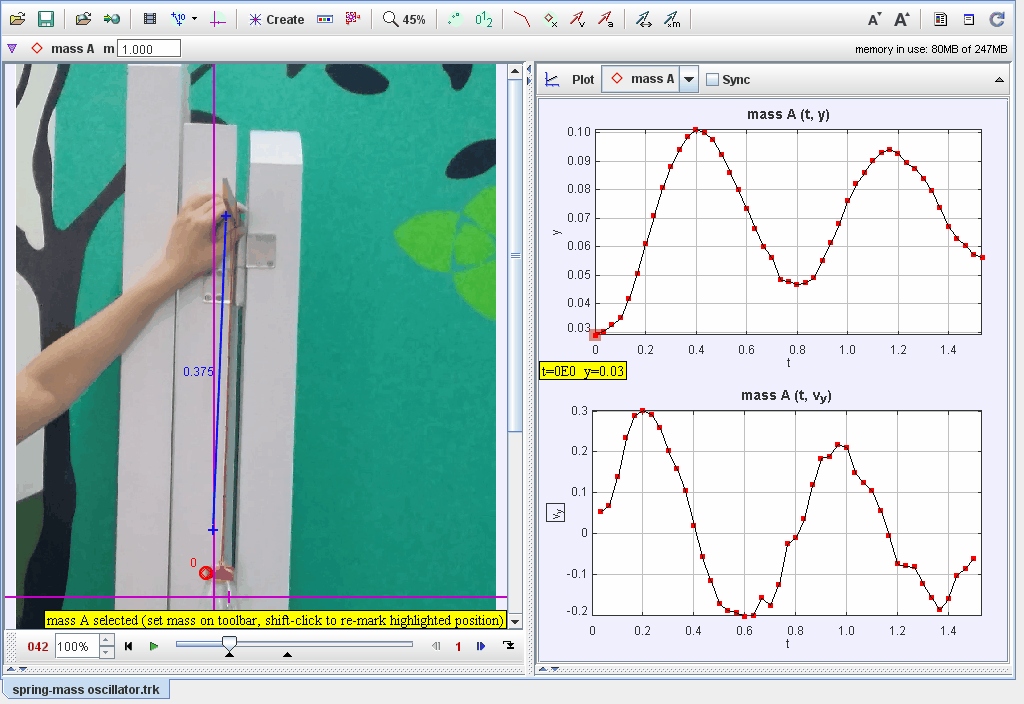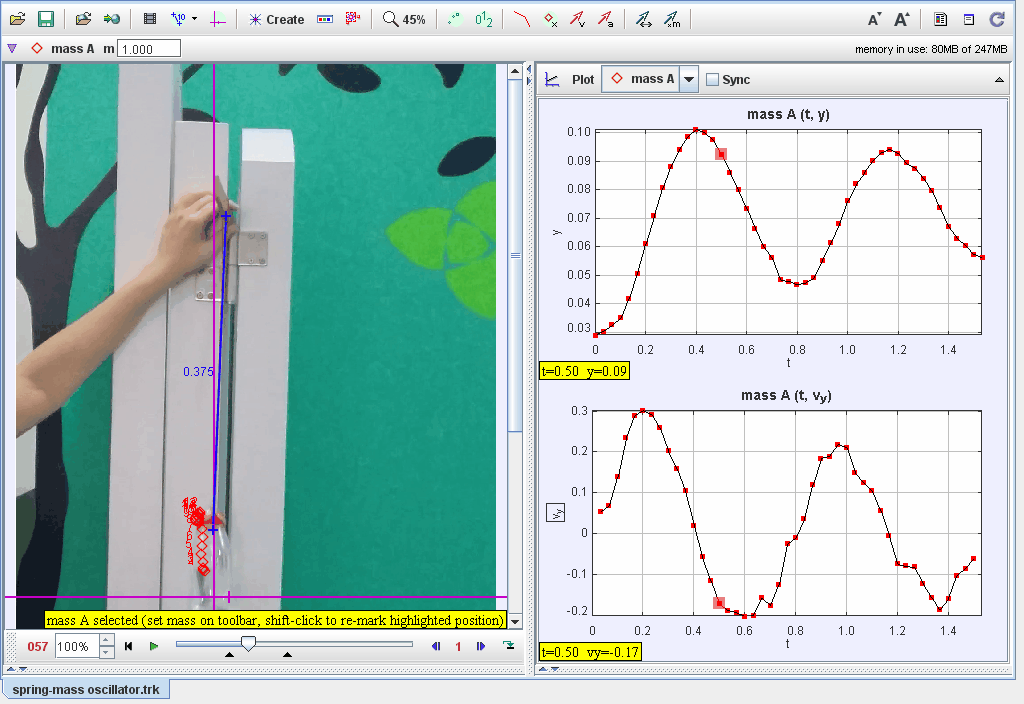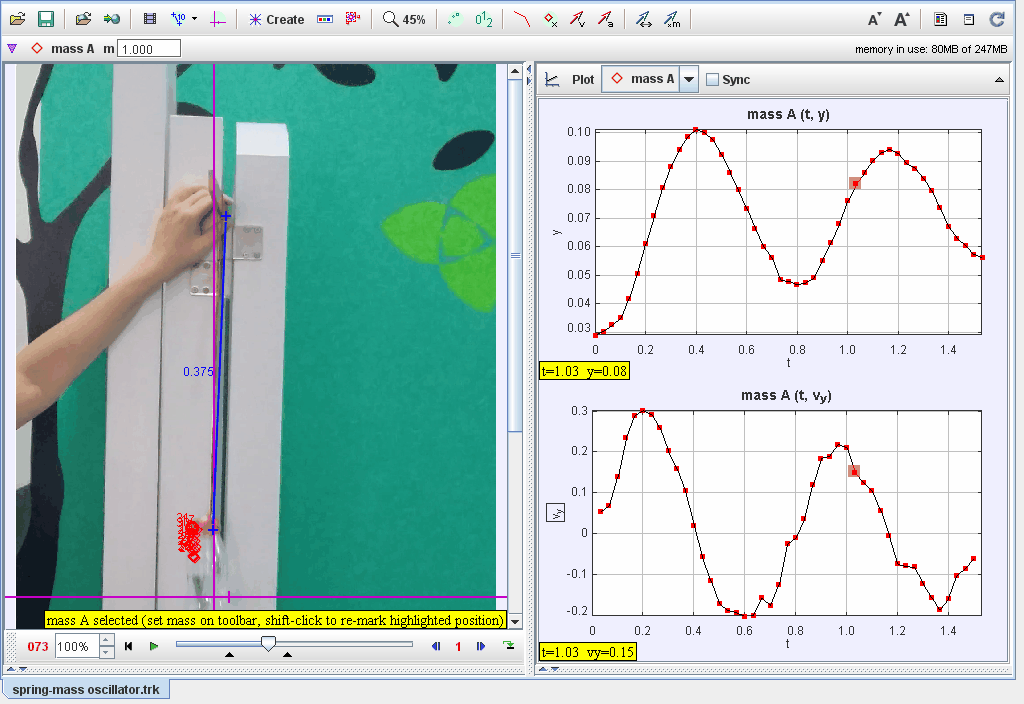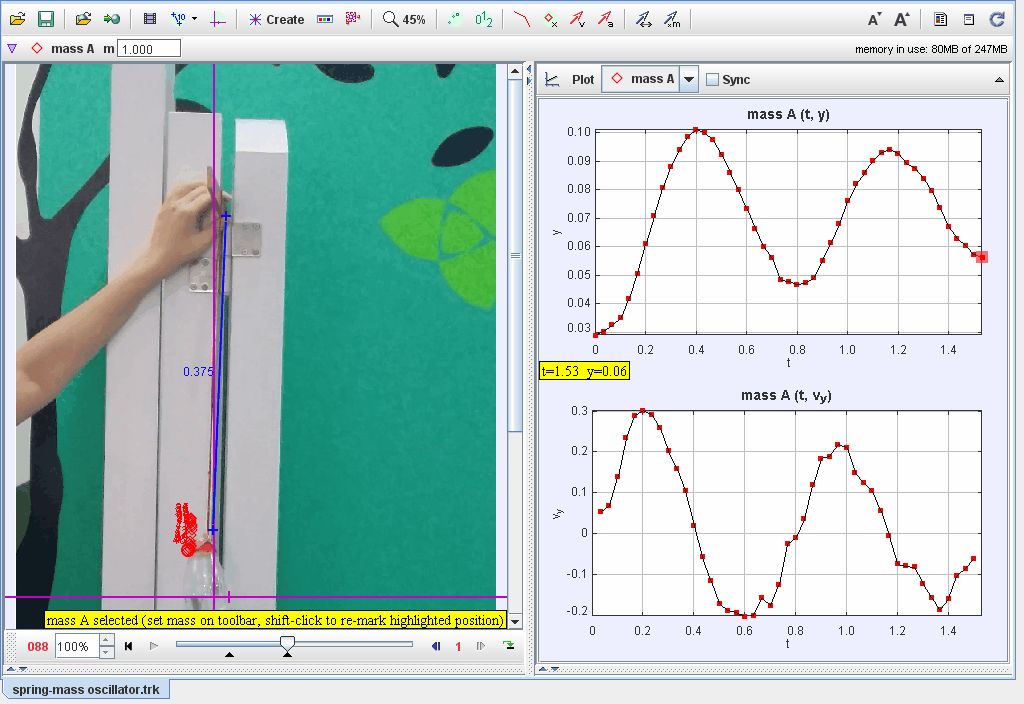
Finding spring constant using rubber bangs and weight. From vy against t graph, find the period. Use w = sqrt (k/m) and calculate k.

For Teachers

- 20151027_144850.mp4

Credits

Author: Qiu Yiru, Khaw Hwee Ju, Chee Wei Wei

Document Brief: Title: "Tracker Mass Oscillating on Thin Rubber"

This document investigates the oscillatory motion of a mass suspended on a thin rubber band, focusing on harmonic motion, damping, and the effects of material elasticity. Observations and models are used to explore the dynamics of the system and the factors influencing its behavior.

Study Guide:

Objective: Analyze the oscillatory motion of a mass on a rubber band, exploring the interplay between elasticity, damping, and harmonic motion.

Key Concepts:

1. Simple Harmonic Motion (SHM):

   • The motion of the system may approximate SHM depending on the linearity of the force-displacement relationship.

2. Elasticity of Rubber:

   • Rubber's elastic properties affect the restoring force and, consequently, the frequency and amplitude of oscillations.

3. Damping:

   • Energy dissipation through heat and internal friction reduces the amplitude over time.

4. Resonance and Natural Frequency:

   • The frequency at which the system naturally oscillates when disturbed.

Experiment Overview:

• Setup: A mass is suspended from a thin rubber band and displaced from its equilibrium position.

• Procedure:

  • Record the motion of the mass using a video tracker or sensor.

  • Measure displacement, velocity, and time to analyze oscillatory behavior.

  • Vary the mass or rubber band properties to study their effects.

• Observation Points:

  • Period and frequency of oscillation.

  • Amplitude decay over time.

  • The relationship between mass, rubber elasticity, and oscillation dynamics.

Questions to Consider:

1. How does the mass affect the frequency and amplitude of oscillations?

   • Answer: Increasing the mass generally decreases the natural frequency of oscillation while potentially increasing the amplitude, assuming the elastic limit of the rubber is not exceeded.

2. What role does rubber elasticity play in the system's behavior?

   • Answer: The elasticity determines the restoring force acting on the mass. A higher elasticity (stiffer rubber) leads to a higher natural frequency and lower amplitude for the same initial displacement.

3. How does damping influence the motion over time?

   • Answer: Damping reduces the amplitude of oscillations over time by dissipating energy as heat or through internal friction within the rubber. This leads to the eventual cessation of motion if no external force is applied.

Applications:

• Understanding elastic properties and damping in materials.

• Designing suspension systems and vibration absorbers.

• Exploring real-world oscillatory systems such as bungee cords and biological tissues.

FAQ:

1. Why study oscillatory motion on rubber? This setup illustrates principles of elasticity, damping, and periodic motion, which have broad applications in physics and engineering.

2. What factors affect the motion of the mass? Mass, rubber band elasticity, initial displacement, and damping properties all play significant roles.

3. What is the significance of the natural frequency? The natural frequency is the rate at which the system oscillates without external forces, providing insights into its elastic properties.

4. Can this experiment demonstrate SHM? The motion approximates SHM if the restoring force is proportional to displacement; deviations occur due to nonlinear elasticity.

5. What practical applications does this study have? Insights are used in material science, engineering designs like shock absorbers, and understanding biological systems such as tendons and ligaments.