About

For Teachers

- mass_spring_damped54.jpg
- mass_spring_damped53.jpg
- mass_spring_damped52.jpg
- mass_spring_damped51.jpg
- mass_spring_damped50.jpg
- mass_spring_damped49.jpg
- mass_spring_damped48.jpg
- mass_spring_damped47.jpg
- mass_spring_damped46.jpg
- mass_spring_damped45.jpg
- mass_spring_damped44.jpg
- mass_spring_damped43.jpg
- mass_spring_damped42.jpg
- mass_spring_damped41.jpg
- mass_spring_damped40.jpg
- mass_spring_damped39.jpg
- mass_spring_damped38.jpg
- mass_spring_damped37.jpg
- mass_spring_damped36.jpg
- mass_spring_damped35.jpg
- mass_spring_damped34.jpg
- mass_spring_damped33.jpg
- mass_spring_damped32.jpg
- mass_spring_damped31.jpg
- mass_spring_damped30.jpg
- mass_spring_damped29.jpg
- mass_spring_damped28.jpg
- mass_spring_damped27.jpg
- mass_spring_damped26.jpg
- mass_spring_damped25.jpg
- mass_spring_damped24.jpg
- mass_spring_damped23.jpg
- mass_spring_damped22.jpg
- mass_spring_damped21.jpg
- mass_spring_damped20.jpg
- mass_spring_damped19.jpg
- mass_spring_damped18.jpg
- mass_spring_damped17.jpg
- mass_spring_damped16.jpg
- mass_spring_damped15.jpg
- mass_spring_damped14.jpg
- mass_spring_damped13.jpg
- mass_spring_damped12.jpg
- mass_spring_damped11.jpg
- mass_spring_damped10.jpg
- mass_spring_damped09.jpg
- mass_spring_damped08.jpg
- mass_spring_damped07.jpg
- mass_spring_damped06.jpg
- mass_spring_damped05.jpg
- mass_spring_damped04.jpg
- mass_spring_damped03.jpg
- mass_spring_damped02.jpg
- mass_spring_damped01.jpg
- mass_spring_damped00.jpg

Credits

Author: Thomas Yeu
Contact: This email address is being protected from spambots. You need JavaScript enabled to view it.

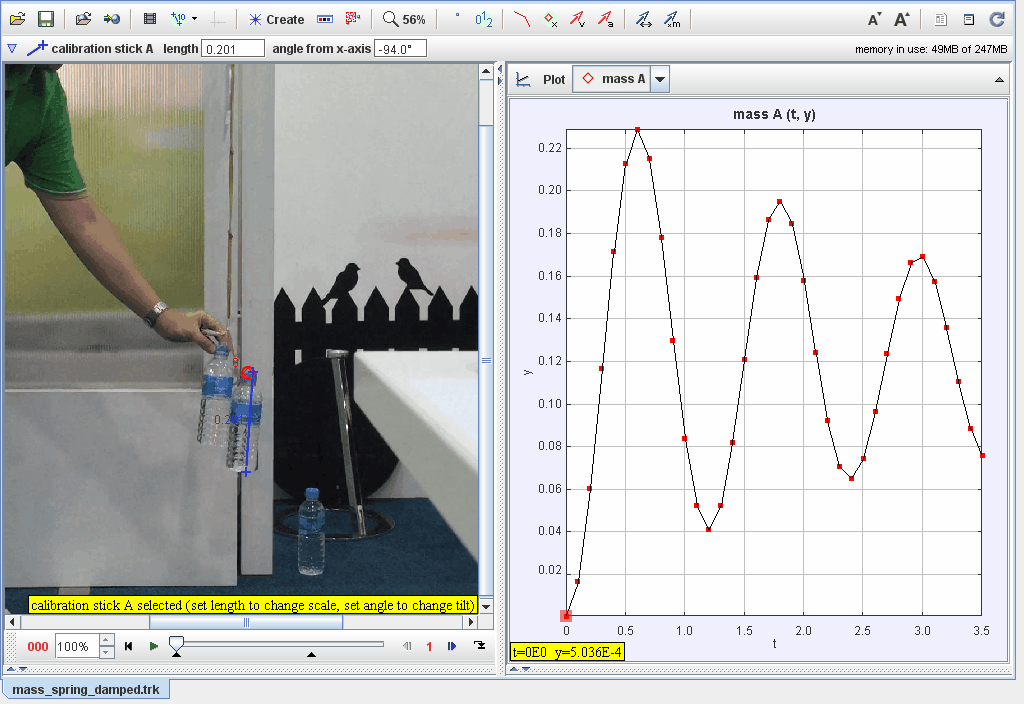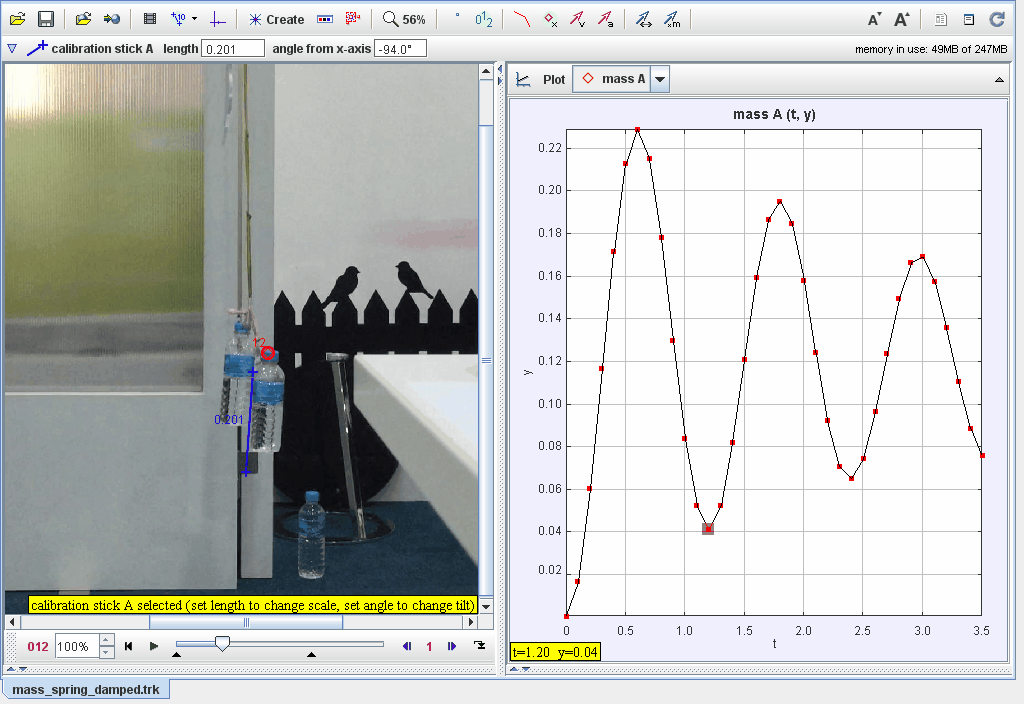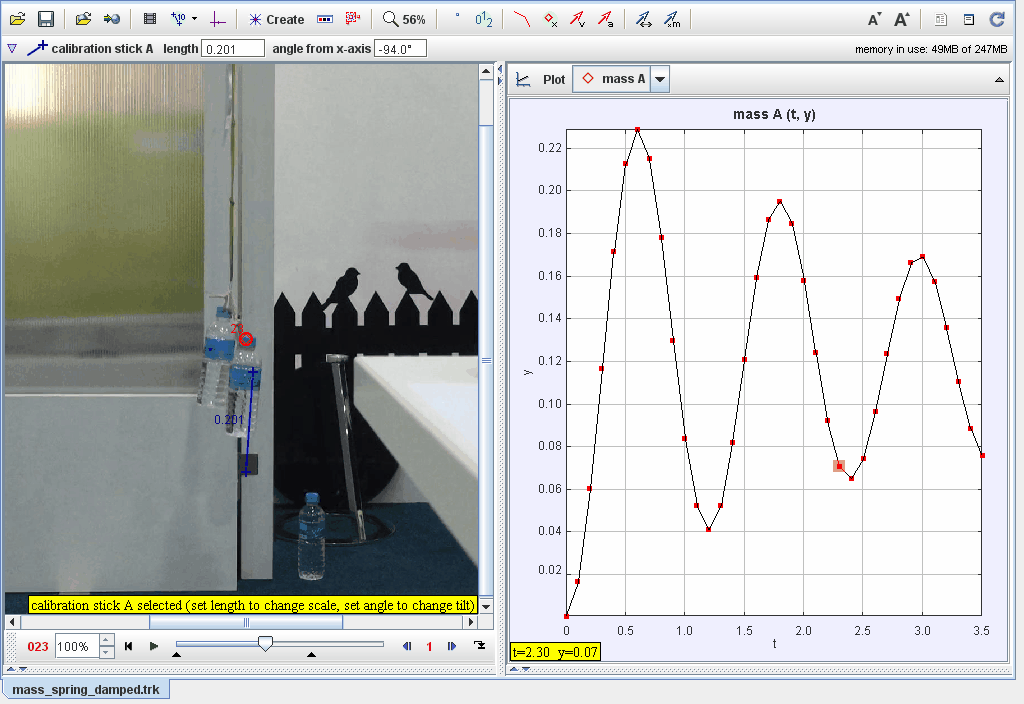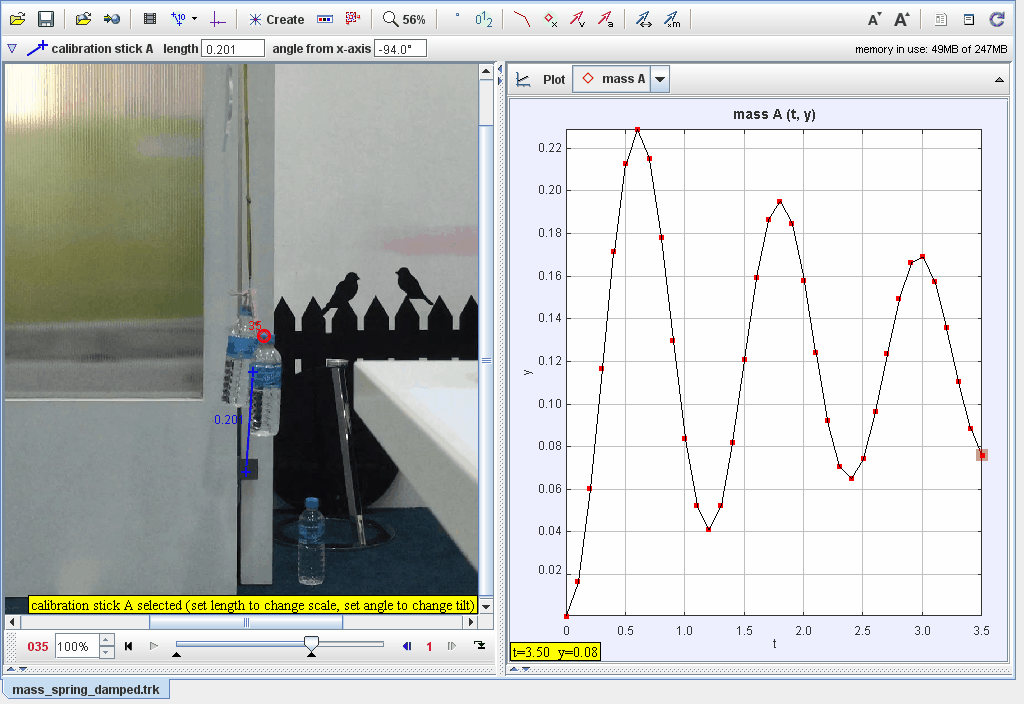
Document Brief: Title: "Tracker 2 Bottles Dampened Oscillation Up and Down"

This document examines the dampened oscillatory motion of two bottles moving up and down in a liquid medium. The focus is on understanding the factors contributing to energy loss, damping rates, and equilibrium shifts. Models and real-world observations are combined to provide a comprehensive analysis.

Study Guide:

Objective: Investigate the dampened oscillatory motion of two bottles moving up and down in a liquid, analyzing energy dissipation, damping effects, and equilibrium dynamics.

Key Concepts:

1. Buoyancy:

   • The upward force exerted by a fluid on an object submerged or partially submerged.

2. Dampened Oscillatory Motion:

   • A repetitive motion where amplitude decreases over time due to energy loss.

3. Damping:

   • The reduction in oscillation amplitude caused by energy loss through fluid resistance or other dissipative forces.

4. Energy Dissipation:

   • The process through which oscillatory energy is converted into other forms, such as heat, due to friction or resistance.

5. Modeling Dynamics:

   • Using physical or computational models to simulate dampened oscillatory motion for predictive analysis.

Experiment Overview:

• Setup: Two bottles are submerged in a liquid and displaced manually to initiate oscillation. The motion is observed until the bottles come to rest.

• Procedure:

  • Observe and record the motion of the bottles as they oscillate and gradually stop.

  • Measure key variables such as amplitude decay, period, and damping rates.

  • Develop a model to simulate the dampening process and compare it with observed behavior.

• Observation Points:

  • The rate at which oscillation amplitude decreases.

  • Interaction effects between the two bottles.

  • Changes in equilibrium position as oscillations cease.

Questions to Consider:

1. What causes the damping effect in the liquid medium?

2. How does the damping rate differ between the two bottles?

3. What insights can the model provide about energy dissipation?

Applications:

• Understanding energy loss in oscillatory systems.

• Designing floating devices that optimize stability and energy dissipation.

• Applying damping principles in engineering, such as in suspension systems and fluid mechanics.

FAQ:

1. Why study dampened oscillations of two bottles? This setup provides insights into energy dissipation and damping, essential concepts in both natural and engineered systems.

2. What determines the damping rate? Damping rate is influenced by factors such as the liquid’s viscosity, the shape and size of the bottles, and their relative positions.

3. How does the interaction affect damping? The presence of two bottles can alter flow patterns and increase or decrease damping rates through interference effects.

4. Can results differ with a different liquid? Yes, changing the liquid’s viscosity or density will affect the damping rate and equilibrium behavior. Models can simulate these conditions for further study.

5. What are practical applications of this study? Insights from this experiment can inform the design of buoys, wave dampers, and other systems that require controlled oscillatory behavior and energy dissipation.