About

Tracker Modeling in 2 Pendulum swinging in phase

For Teachers

- Pendulum_1inPhase.mp4

Credits

Author: lookang model and jitning video
Contact: This email address is being protected from spambots. You need JavaScript enabled to view it.

Document Brief: Modeling Two Pendulums Swinging in Phase Using Tracker

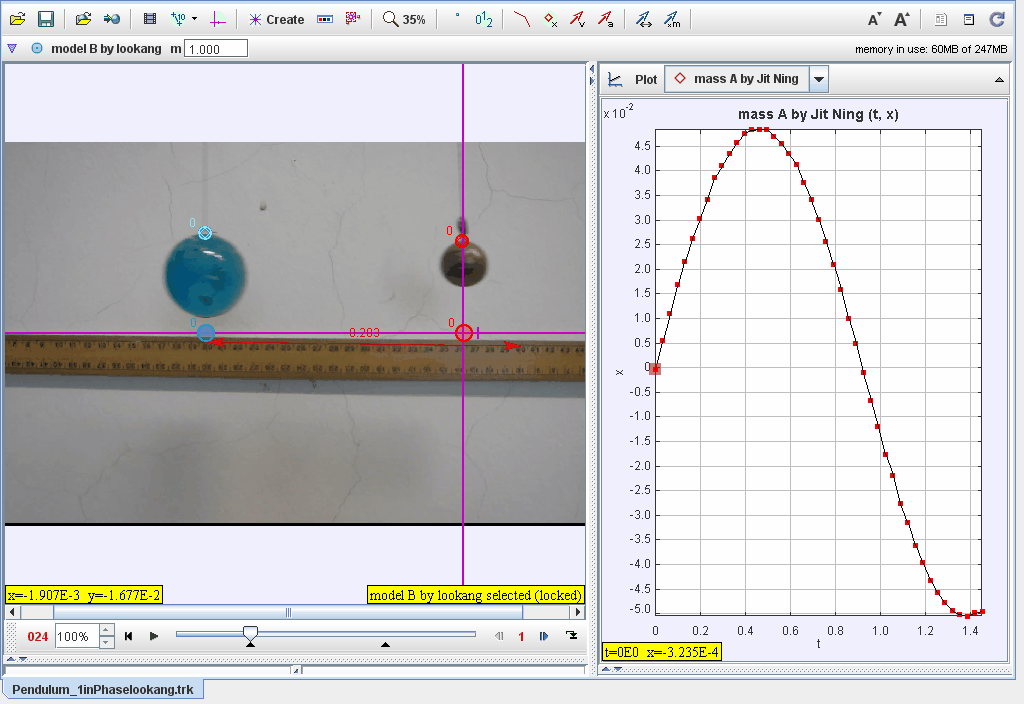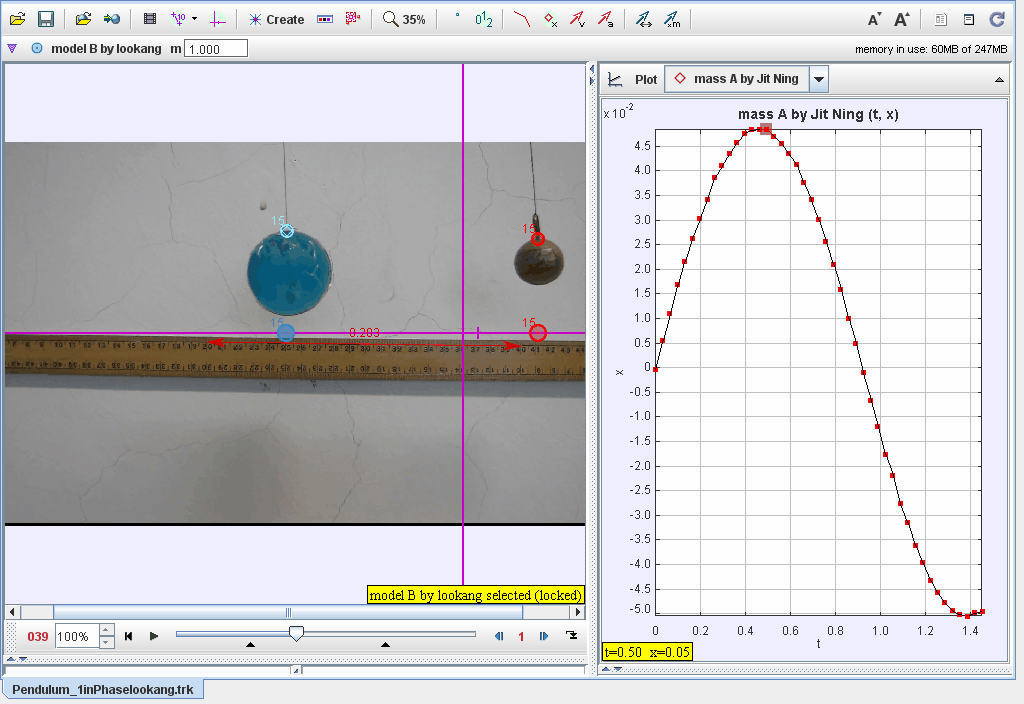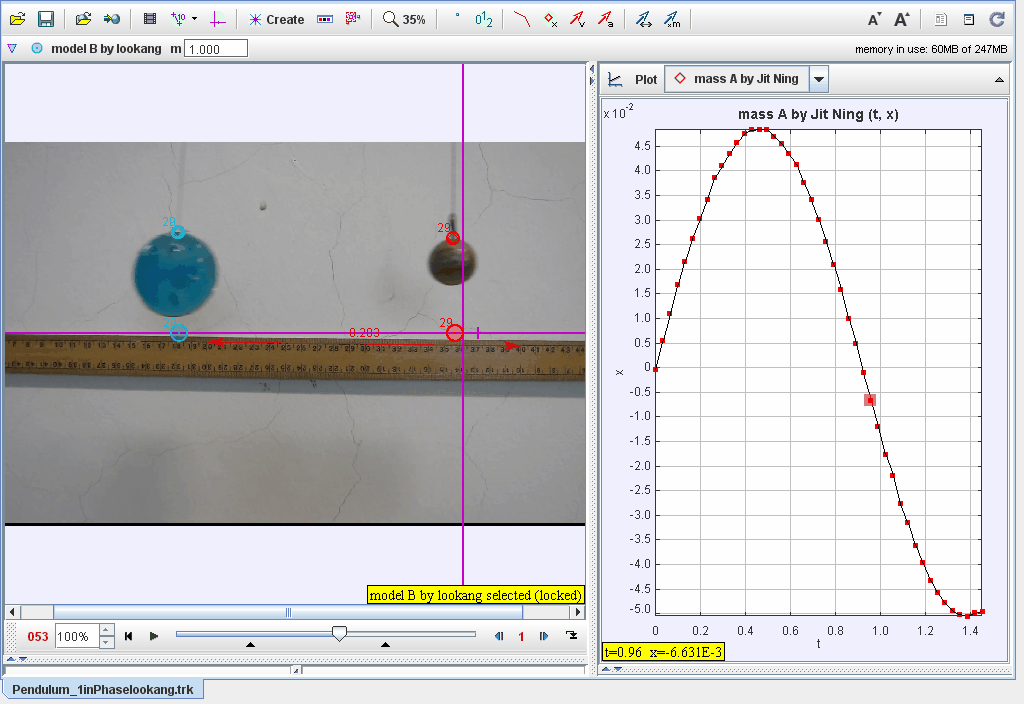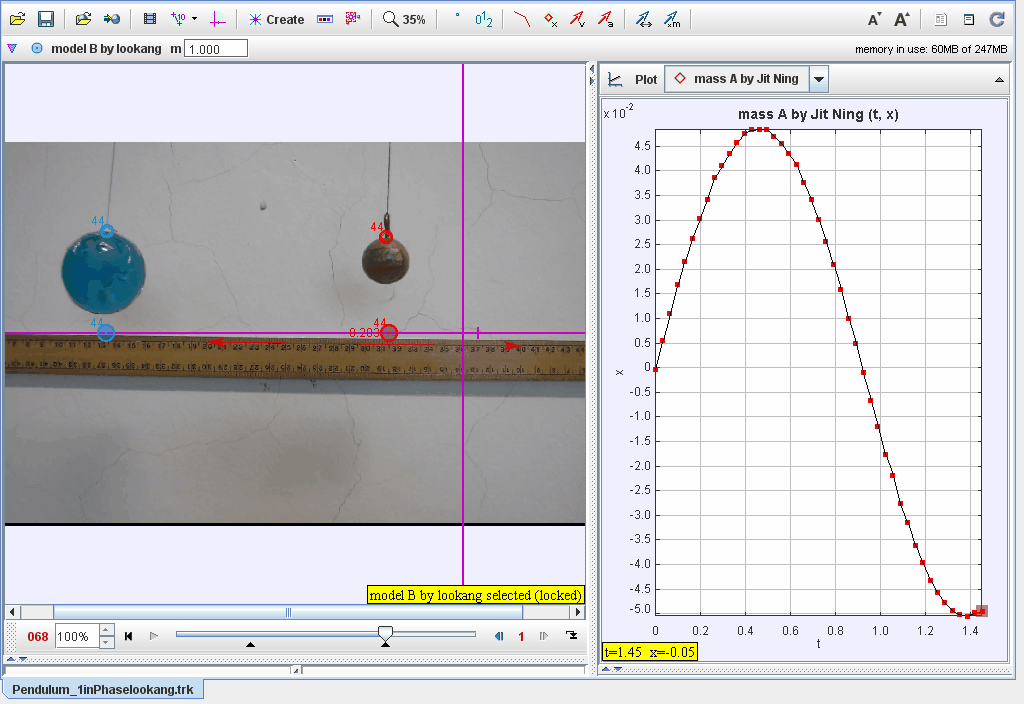
This document describes the analysis of two pendulums swinging in phase, modeled using Tracker software. The motion is analyzed in Cartesian coordinates, with position functions describing the periodic motion of the pendulums. The focus is on their synchronized motion and the phase relationships between displacement and time.

Purpose:

To explore the periodic motion of two pendulums swinging in phase, analyzing their displacement, velocity, and synchronization using Tracker’s modeling tools.

Key Features:

• Position functions applied to describe the motion:
  • $x=A\sin (\omega t+\varphi )$ for each pendulum.
• Graphical analysis of displacement ($x,y$) over time.
• Comparison of theoretical position functions with experimental data.

Study Guide: Modeling In-Phase Pendulum Motion

Learning Objectives:

1. Understand the synchronized motion of pendulums swinging in phase.
2. Analyze displacement ($x$) vs. time ($t$) graphs to validate periodic motion.
3. Explore the relationship between position functions and experimental motion tracking.

Step-by-Step Guide:

1. Setup and Calibration:

   • Import the video of the two pendulums swinging in phase into Tracker.
   • Calibrate the coordinate system using the ruler in the video for accurate scaling.

2. Tracking Motion:

   • Track the position of each pendulum bob frame by frame.
   • Record displacement data along the $x$-axis for both pendulums.

3. Define Position Functions:

   • Open Tracker’s Model Builder.
   • For each pendulum, define the position function:
     • $x=A\sin (\omega t+\varphi )$, where:
       • $A=0.049$ m (amplitude),
       • $\omega =3.378$ rad/s (angular frequency),
       • $\varphi =0.018$ rad (phase offset).
     • $y=0$ (motion restricted to horizontal).

4. Graphical Analysis:

   • Plot $x$-displacement vs. $t$:
     • Observe the sinusoidal behavior characteristic of periodic motion.
     • Verify that both pendulums swing in phase (matching peaks and troughs).
   • Analyze the phase relationship between the pendulums, ensuring synchronization.

5. Applications:

   • Study coupled oscillatory systems, such as pendulum clocks or synchronized metronomes.
   • Explore how external forces or damping affect phase synchronization.

Tips for Success:

• Ensure accurate tracking of both pendulums for reliable analysis.
• Validate the position function parameters by comparing theoretical and experimental data.

FAQ: Two Pendulums Swinging in Phase

1. Why are the pendulums swinging in phase?

In-phase motion means the pendulums reach their maximum displacement simultaneously, maintaining synchronized oscillations.

2. What does the position function $x=A\sin (\omega t+\varphi )$ represent?

This function describes the periodic motion of each pendulum, with amplitude ($A$), angular frequency ($\omega$), and phase offset ($\varphi$) determining the motion’s characteristics.

3. How do you verify synchronization?

By plotting $x$-displacement vs. $t$ for both pendulums and ensuring their peaks and troughs occur simultaneously.

4. What is the role of angular frequency ($\omega$)?

Angular frequency determines the speed of oscillation and is related to the pendulum’s period by T=2πωT = \frac{2\pi}{\omega}T=ω2π​.

5. Can this model handle damping or external forces?

Not directly. The current model assumes ideal periodic motion without damping or external forces. Modifications can include damping terms if needed.

6. What are the practical applications of this analysis?

• Understanding coupled oscillatory systems in physics and engineering.
• Designing synchronized systems, such as metronomes or pendulum clocks.
• Exploring phase synchronization in natural systems like biological rhythms.