About

This email address is being protected from spambots. You need JavaScript enabled to view it.

For Teachers

- V_20150806_140559.mp4

Credits

Author: Eka Cahya Prima
Contact: This email address is being protected from spambots. You need JavaScript enabled to view it.

Rolling Cylinders 501 (Master-Level Dynamics) by Eka Cahya Prima"

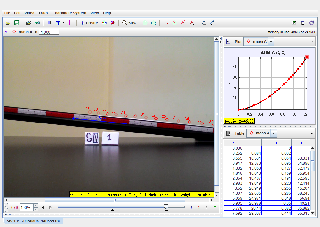
This advanced study investigates the intricate physics of rolling cylinders, focusing on high-precision modeling, chaotic interactions, and the application of non-linear dynamics principles. The experiments explore systems with irregular shapes, non-uniform mass distributions, and variable environmental conditions. Tracker software is used extensively for data collection, analysis, and dynamic simulation.

Study Guide:

Objective:

• Understand the effects of irregularities and environmental variability on rolling dynamics.
• Explore chaotic systems and their implications for real-world applications.

Key Concepts:

1. Non-Linear Dynamics:

   • Understanding non-linear relationships between force, motion, and geometry in rolling systems.

2. Irregular Shapes and Mass Distributions:

   • How non-uniform shapes and masses alter rolling stability and trajectories.

3. Chaotic Interactions:

   • Studying systems that exhibit sensitivity to initial conditions and unpredictable long-term behavior.

4. Dynamic Simulations:

   • Using Tracker software to simulate and predict motion in advanced rolling systems.

Experiment Overview:

• Setup:
  Rolling experiments include cylinders with varied shapes, mass distributions, and material properties, conducted on complex surfaces with variable inclines. Tracker software and high-precision sensors capture motion details.

• Procedure:

  1. Roll irregularly shaped cylinders on complex surfaces.
  2. Introduce disturbances to observe sensitivity and chaos.
  3. Analyze motion data to identify patterns and anomalies.
  4. Simulate advanced systems using Tracker for predictive modeling.

• Observation Points:

  • Irregular path dynamics.
  • Stability under varying conditions.
  • Identification of chaotic behaviors.

Questions to Consider:

1. How do irregular shapes affect rolling dynamics?

   • Answer: Irregular shapes create uneven moments of inertia and varying frictional forces, leading to unique rolling behaviors.

2. What is the role of chaos in rolling systems?

   • Answer: Chaotic systems demonstrate high sensitivity to initial conditions, causing small variations to significantly alter motion over time.

3. How does mass distribution influence stability?

   • Answer: Uneven mass distribution shifts the center of mass, affecting balance and trajectory.

4. Can rolling patterns be predicted in non-linear systems?

   • Answer: While precise predictions are challenging, simulations can provide probabilistic insights and trend analysis.

5. How does Tracker software enhance understanding of chaos?

   • Answer: Tracker captures detailed motion data that allows for in-depth analysis of seemingly random behaviors.

Applications:

• Physics Research: Insights into non-linear dynamics and chaotic systems.
• Engineering: Design of rolling components for irregular terrains and non-standard applications.
• Material Science: Studying effects of irregularities in manufactured components.

FAQ:

1. Why study irregular and chaotic rolling systems?

   • Real-world systems often feature irregularities and unpredictability, making these studies highly applicable.

2. What challenges are associated with these experiments?

   • Controlling and measuring small irregularities and predicting chaos require advanced equipment and analytical tools.

3. Can Tracker predict chaotic behaviors?

   • Tracker provides data for modeling and trend analysis, which helps in understanding chaotic dynamics indirectly.

4. What are practical benefits of these studies?

   • Improved designs for rolling systems in uneven environments and a better understanding of material behaviors.

5. How can this study be expanded further?

   • Incorporate AI-based simulations for more robust predictions and explore multi-body chaotic systems for broader insights.

Research

http://scitation.aip.org/content/aip/proceeding/aipcp/10.1063/1.4941183 Kinematics investigations of cylinders rolling down a ramp using tracker Eka Cahya Prima1,2,*, Menurseto Mawaddah1, Nanang Winarno1 andWiwin Sriwulan3