About

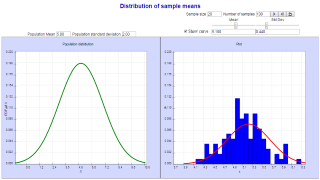
This applet demonstrates what happens when many samples are taken repeatedly from a population of fixed normal distribution.

1. Choose the mean and standard deviation of the population.

2. Choose the sample size and number of samples you wish to take.

3. Press "play". The applet will generate the random samples and keep a tally of their means.

4. Click on the checkbox to see another Gaussian curve. Try and adjust its mean and standard deviation to determine the best fit for the histogram. (Note: y-values are scaled so that the curve's height is comparable to the histogram's.)

 

Credits

Boon Leong Ng; Francisco Esquembre