About

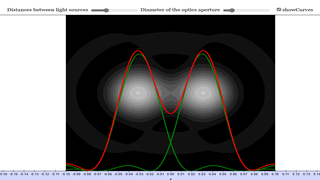
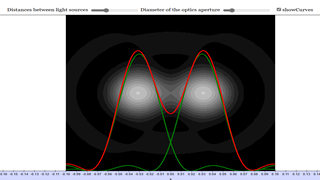
Optical Resolution

The EJS Optical Resolution model computes the image from two point sources as seen through a circular aperture such as a telescope or a microscope.  The simulation allows the user to vary the distance between the light sources and the diameter of the aperture, as well as the intensity of the light source. For a single point source, the central circular maximum, called the diffraction spot or Airy disk, has an angular half width determined by

For two point sources, as the distance between the point decreases, the diffraction patterns begin to overlap until eventually they become undistinguishable and it is no longer possible to determine if there are one or two images. According to the Rayleigh criterion, two images are resolvable when the center of the diffraction maximum of one image is aligned with the first minimum in the diffraction pattern of the second image.

References:

• Giancoli Physics: Principles with Applications sixth edition, 711-713.

Credits:

The aperture simulation was created by Fu-Kwun Hwang using the Easy Java Simulations (EJS) modeling tool.  It was adapted to EJS version 4.0 by Robert Mohr at Davidson College.  You can examine and modify the model for this simulation if you have Ejs installed by right-clicking within the wave function plot and selecting "Open Ejs Model" from the pop-up menu.  Information about EJS is available at: <http://www.um.es/fem/Ejs/> and in the OSP ComPADRE collection <http://www.compadre.org/OSP/>.

 

Translations

Code	Language		Translator	Run

Credits

Fu-Kwun Hwang; lookang

Sample Learning Goals

[text]

For Teachers

[text]

Research

link https://sg.iwant2study.org/ospsg/index.php/1259

 

 

 

 

Exploring the Optical Resolution Model: A Conversion to EJS JavaScript

The Optical Resolution Model, originally created by Fu-Kwun Hwang and edited by Robert Mohr and now converted to EJS Javascript 6.1 by lookang, provides a powerful tool for understanding how two point sources of light are resolved when viewed through a circular aperture. This simulation mirrors real-world instruments like telescopes or microscopes, where diffraction plays a crucial role in determining the clarity and separation of objects. The model, now converted from EJS Java to EJS JavaScript, retains its core functionality while allowing broader accessibility on modern web platforms.

What the Optical Resolution Model Does

The model computes how two point light sources appear through a circular aperture. In practice, this simulates the diffraction pattern created by light as it passes through an aperture (such as in a telescope or microscope), where light waves interfere, creating an airy disk pattern. Users of this simulation can interact with several parameters:

• Distance between the light sources: Increasing the distance makes the two sources easier to distinguish.
• Diameter of the aperture: Larger apertures reduce the effects of diffraction, improving resolution.
• Intensity of the light source: This allows exploration of how brightness impacts visibility and resolution.

This model is ideal for demonstrating optical resolution and can be specifically used to illustrate the Rayleigh criterion.

Understanding the Rayleigh Criterion with the Model

The Rayleigh criterion is a key concept in optics, used to define the minimum resolvable distance between two light sources. It states that two sources are just resolvable if the center of the diffraction pattern (Airy disk) from one source coincides with the first minimum of the diffraction pattern from the other. In simpler terms, it tells us when two closely spaced objects can be distinguished as separate.

With the Optical Resolution Model, users can visually explore this criterion. By adjusting the aperture size and the distance between the sources, users can simulate how two point sources blur into one another as they get closer. The simulation allows a hands-on understanding of how the diffraction limit affects resolution, making it easier for students or researchers to grasp the complex interplay of optics and diffraction.

Transition from EJS Java to EJS JavaScript

The move from EJS Java to EJS JavaScript is significant and I used EJS 5.33 to open the old Java file to convert to JavaScript. Originally, this simulation was built in the now-outdated Java-based EJS framework, which required the installation of Java plugins to run. With the shift to JavaScript, the model is now platform-independent, functioning on any modern browser without requiring additional plugins. This allows easier integration into web-based educational platforms and broadens access to learners and educators globally.

The EJS 6.1 Scalar Field Element

https://www.um.es/fem/wikis/runwebejs/?url=https://iwant2study.org/lookangejss/04waves_11superposition/ejss_model_OpticalResolution.zip

A key enhancement in EJS 6.1, introduced by Felix, is the addition of a Scalar Field element. This new feature allows users to convert the old scalar fields used in Java-based EJS simulations directly into EJS 6.1 JavaScript models. The scalar field element is a critical tool for handling mathematical fields, like the intensity distribution in the Optical Resolution Model.

Fortunately, this feature is NOW available in EJS 6.02 or webEJS, making webEJS or EJS 7.1 the go-to version for users looking to preserve complex field behaviors during their migration from Java to JavaScript simulations. This addition bridges a significant gap for developers and educators who need to port over older models without losing functionality or precision, ensuring that even legacy simulations continue to serve as valuable educational tools.

Conclusion

The Optical Resolution Model is an invaluable educational tool for visualizing concepts like the Rayleigh criterion and understanding diffraction through apertures. The transition to EJS JavaScript ensures that this simulation continues to be accessible in a modern web environment. Additionally, the introduction of the Scalar Field element in EJS 7.1 opens the door for smoother transitions of older Java models, keeping them relevant for today's educators and students.

As we continue to explore the boundaries of optics and resolution, simulations like this provide essential hands-on learning experiences. The blend of modern web technology with established educational models makes this an exciting time for educators seeking to integrate simulation-based learning into their curriculum.

 

Video

[text]

 Version:

1. https://weelookang.blogspot.com/2024/09/exploring-optical-resolution-model-for.html

Other Resources

https://www.geogebra.org/m/hmzyudh9

end faq

{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}