About

1.2 Definitions, equations and graphs 

1.2.1 Definition of Simple Harmonic Motion (SHM):           LO (d)

A motion where the  acceleration a of an object is always directed towards a fixed point ( the equilibrium position O ) and proportional to its displacement x from the fixed point is said to be  be simple harmonic. 

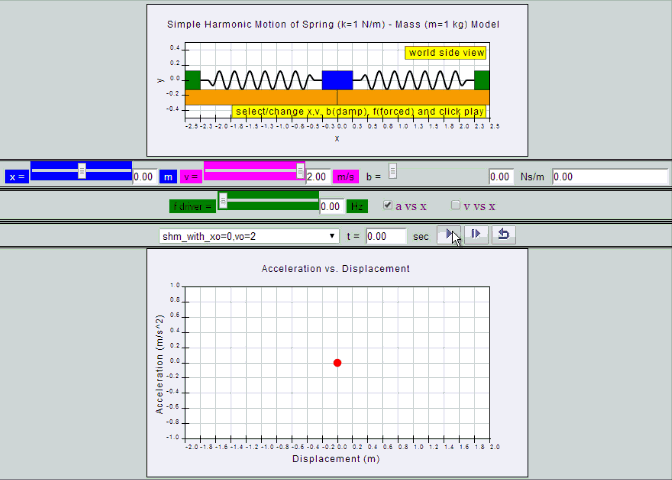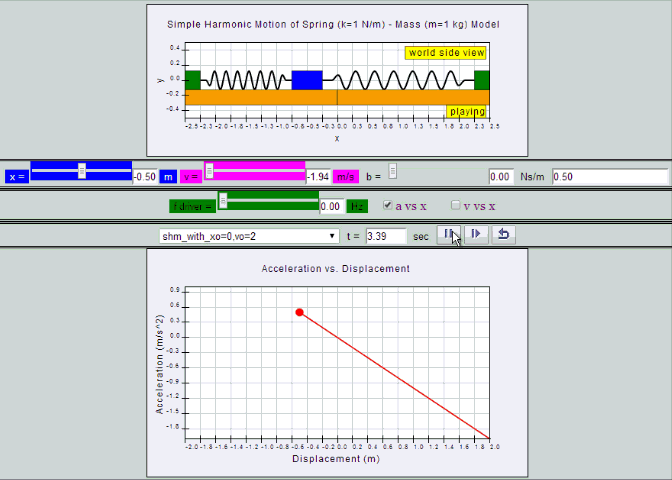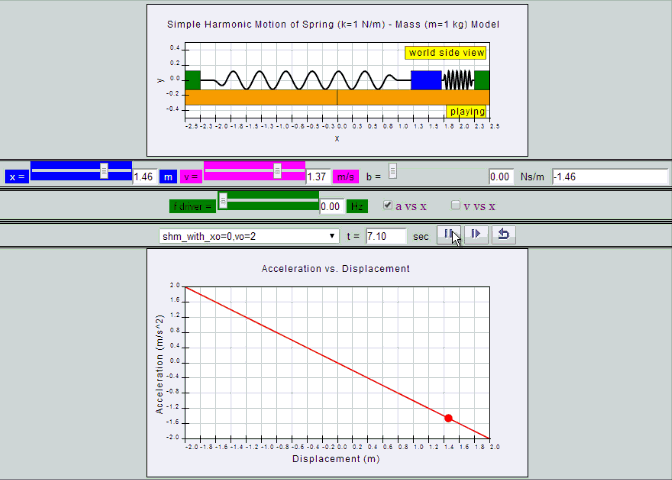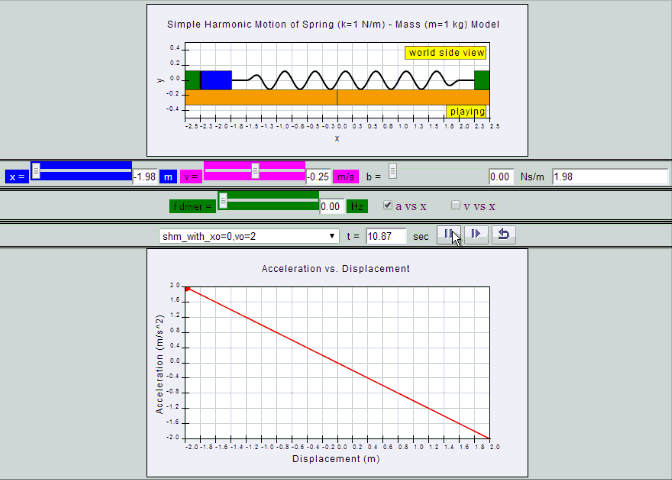
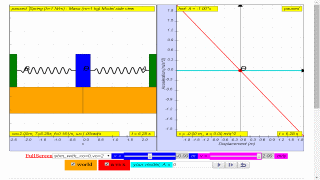
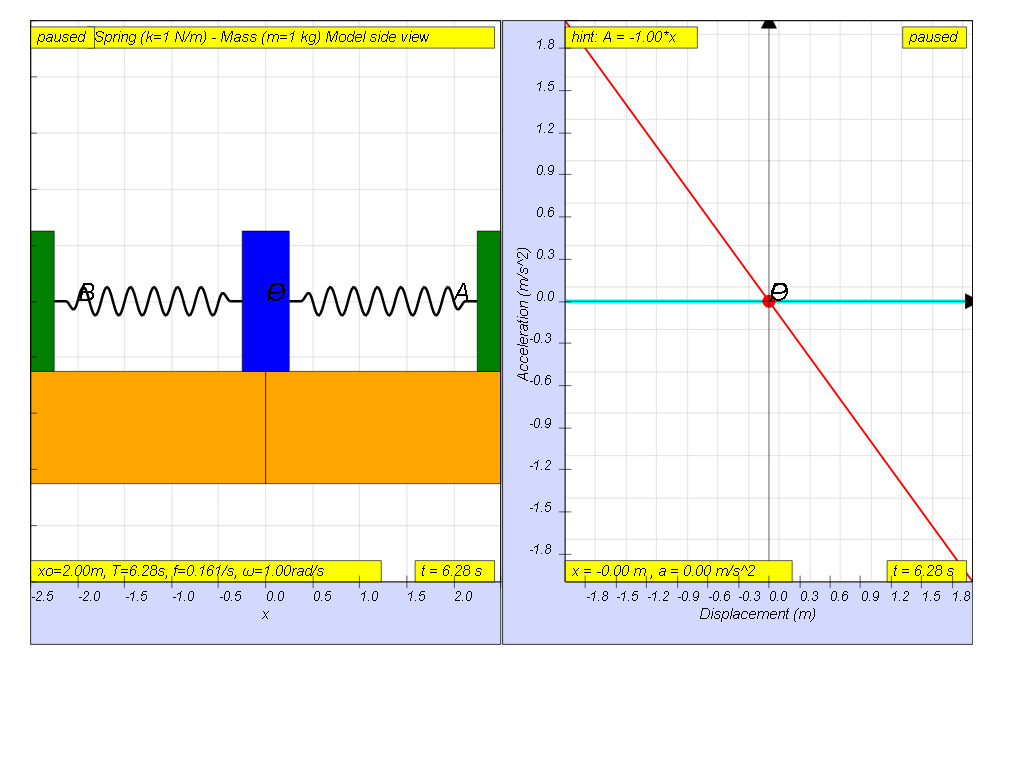
        Defining equation of SHM

a =  - ω² x

Observe from the model or the animation, suggest the reason for the negative sign.

The negative sign means a is always directed towards the equilibrium point while x is pointing away from equilibrium point O.

In other words a and x are in the opposite direction.                                         

1.2.1.1 Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/70

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.; Francisco Esquembre

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM07/SHM07_Simulation.xhtml

Briefing Document: ⚛️Simple Harmonic Motion Simulation Applet

Subject: Analysis of Simple Harmonic Motion (SHM) and associated simulation applet.

Source: Excerpts from "10.2 Definition of Simple Harmonic Motion and Horizontal Spring Mass Model A vs X JavaScript HTML5 Applet Simulation Model - Open Educational Resources / Open Source Physics @ Singapore"

Date: October 26, 2024

1. Introduction

This document provides an overview of the definition of Simple Harmonic Motion (SHM), as presented on the Open Educational Resources / Open Source Physics @ Singapore website, focusing specifically on the description accompanying a JavaScript HTML5 applet simulation. The source material is primarily concerned with defining SHM and providing a tool for visualizing it via a spring-mass system.

2. Core Definition of Simple Harmonic Motion

The document clearly defines Simple Harmonic Motion as follows:

"A motion where the acceleration a of an object is always directed towards a fixed point (the equilibrium position O) and proportional to its displacement x from the fixed point is said to be be simple harmonic."

Key elements of this definition:

• Fixed Point (Equilibrium Position): SHM is always relative to a central equilibrium point. The object oscillates back and forth around this point.
• Acceleration Towards Equilibrium: The acceleration of the object is not constant; it always points towards the equilibrium position, not away from it. This is a crucial characteristic.
• Proportionality to Displacement: The magnitude of the acceleration is directly proportional to the object's displacement from the equilibrium point. The further the object is from equilibrium, the greater the restoring acceleration.

3. Defining Equation of SHM

The defining equation for SHM is given as:

"a = - ω² x"

Where:

• a represents acceleration.
• ω (omega) represents the angular frequency (a constant for a specific SHM system)
• x represents the displacement from the equilibrium position.

4. Significance of the Negative Sign

The negative sign in the equation a = - ω² x is crucial:

"The negative sign means a is always directed towards the equilibrium point while x is pointing away from equilibrium point O. In other words a and x are in the opposite direction."

This highlights the restoring force characteristic of SHM. As the object moves away from the equilibrium point, the acceleration always tries to pull it back towards that point. The displacement x is measured relative to the equilibrium, and acceleration is always in the opposite direction of the displacement, hence the negative sign.

5. Simulation Applet and Associated Resources

The source provides the following:

• Embedded Applet: An embedded iframe provides direct access to the interactive SHM simulation, which is hosted at https://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM07/SHM07_Simulation.xhtml.
• Link to Source Code: A link to the index page http://iwant2study.org/ospsg/index.php/70
• Android App: A link to the app in the google play store:https://play.google.com/store/apps/details?id=com.ionicframework.shm07app810976&hl=en
• Geogebra Tutorial: A link to a geogebra tutorial https://www.geogebra.org/m/zHj8G43r

6. Context and Related Educational Resources

The document is presented within a context of other interactive educational resources, including simulations and tutorials. There are a great number of other simulations that are part of the Open Educational Resources / Open Source Physics @ Singapore resource and are listed following the main content, showing the breadth of the simulations available. Many of these simulations focus on mechanics and motion, and a selection are:

• Energy Pendulum Model
• Ferris Vertical Circular Wheel
• Newton Cradle (3D)
• Collision Carts
• Projectile Motion and Kinematics simulations

This context indicates a commitment to active learning through interactive simulations and visual aids.

7. Key Takeaways

• Simple Harmonic Motion (SHM) is defined by a specific relationship between an object's acceleration and displacement.
• The acceleration is always directed towards the equilibrium point and is proportional to the displacement from that point.
• The negative sign in the defining equation a = - ω² x is fundamental and signifies the restoring force characteristic of SHM.
• Interactive simulations, such as the provided applet, are used to help students understand the concept and explore the phenomena.
• The website is part of a large collection of free simulation applets for a range of physics topics.

8. Conclusion

The provided source offers a concise, yet thorough definition of Simple Harmonic Motion and makes available an interactive simulation to aid in understanding. The negative sign within the mathematical equation is well-explained. The emphasis on visual aids and interactive tools supports a practical, active approach to learning about SHM. The vast range of other simulations provides evidence that this website is a major source for physics based educational applets.

Simple Harmonic Motion Study Guide

Quiz

Instructions: Answer the following questions in 2-3 sentences each.

1. What is the defining characteristic of simple harmonic motion (SHM)?
2. In the equation a = -ω²x, what does 'a' represent?
3. In the same equation, what does 'x' represent?
4. What does the negative sign in the equation a = -ω²x signify about the relationship between acceleration and displacement?
5. What is the significance of the fixed point (equilibrium position) in SHM?
6. Describe the direction of acceleration relative to the equilibrium point in SHM.
7. Describe the direction of displacement in SHM relative to the equilibrium point.
8. Explain why a spring mass system can demonstrate SHM.
9. What does ω represent in the SHM equation?
10. If displacement and acceleration are always in opposite directions, what does that tell us about the velocity?

Quiz Answer Key

1. Simple Harmonic Motion (SHM) is a type of motion where an object's acceleration is always directed towards a fixed point (equilibrium) and is directly proportional to the object’s displacement from that fixed point. It's a specific type of oscillatory motion.
2. In the equation a = -ω²x, 'a' represents the acceleration of the object undergoing Simple Harmonic Motion. It is a measure of how quickly the velocity of the object is changing.
3. In the equation a = -ω²x, 'x' represents the displacement of the object from its equilibrium position. It is the distance and direction of the object from the point of rest or center.
4. The negative sign in the equation a = -ω²x signifies that the acceleration (a) and the displacement (x) are always in opposite directions. This means that when the object is displaced to the right of equilibrium, its acceleration is to the left, and vice versa.
5. The fixed point (equilibrium position) is crucial in SHM because it's the point toward which the restoring force, and therefore the acceleration, is always directed. The system oscillates around this point.
6. In SHM, the acceleration is always directed toward the equilibrium point. This means that when the object is displaced to one side, the acceleration will push it back toward the center.
7. In SHM, the displacement is away from the equilibrium point. It measures how far an object has moved from the center or the resting position.
8. A spring mass system demonstrates SHM because when the spring is stretched or compressed, it exerts a restoring force proportional to the displacement. This force always acts towards the equilibrium position, fulfilling the conditions of SHM.
9. ω represents the angular frequency of the simple harmonic motion. It determines the speed of the oscillation, a value that can be derived from the period (T) or the frequency (f).
10. If displacement and acceleration are always in opposite directions, then it tells us that the object is always accelerating toward the equilibrium position even if the object is moving away from it. When the object reaches maximum displacement, its velocity is momentarily zero, before it changes direction and the process is repeated.

Essay Questions

Instructions: Answer each question in a detailed, well-organized essay.

1. Explain the relationship between the defining equation of SHM (a = -ω²x) and the behavior of a spring-mass system. Discuss how the force exerted by the spring leads to the specific conditions of SHM.
2. Compare and contrast the concepts of displacement and acceleration in the context of SHM. How do their changing magnitudes and directions contribute to the oscillatory nature of the motion?
3. Using a diagram of a mass on a horizontal spring, explain the negative sign in the SHM equation. Discuss how this sign mathematically represents the relationship between the object's position and its acceleration.
4. Analyze the energy transformations that occur during simple harmonic motion of a spring-mass system. Consider the relationship between potential energy, kinetic energy, and total energy throughout the cycle.
5. Discuss the significance of SHM as a model in physics. In what ways is this an oversimplified example of periodic motion, and where else is it useful to understand and represent physical phenomena?

Glossary

Simple Harmonic Motion (SHM): A type of periodic motion where the restoring force is directly proportional to the displacement and acts in the opposite direction. The acceleration of an object is always directed toward a fixed point (equilibrium position) and is proportional to its displacement from that point.

Equilibrium Position: The central or resting position of an object in SHM, where the net force acting on the object is zero. It’s the point toward which the object's acceleration is always directed.

Displacement (x): The distance and direction of an object from its equilibrium position. This is typically measured along the path of the object’s movement.

Acceleration (a): The rate of change of velocity of an object with respect to time. In SHM, it’s always directed toward the equilibrium position and is proportional to the object’s displacement.

Angular Frequency (ω): A measure of how fast an oscillation is occurring. It’s related to the period (T) and frequency (f) of the oscillation by the formulas ω = 2π/T or ω=2πf.

Restoring Force: The force that acts to bring an object back to its equilibrium position. In SHM, this force is directly proportional to the displacement and acts in the opposite direction.

Apps

https://play.google.com/store/apps/details?id=com.ionicframework.shm07app810976&hl=en

Video

https://notebooklm.google.com/notebook/9746bd95-94dc-4305-acbc-4445bce5094a/audio

Other Resources

1. https://www.geogebra.org/m/zHj8G43r Simple Harmonic Motion Tutorial by ukukuku

FAQs about Simple Harmonic Motion and Interactive Simulations

1. What is Simple Harmonic Motion (SHM)? Simple Harmonic Motion is a specific type of oscillatory motion where an object's acceleration is always directed toward a fixed equilibrium point, and the magnitude of this acceleration is directly proportional to the object's displacement from that point. Essentially, the restoring force (and thus, the acceleration) pulls the object back towards the center, and the farther away it is, the stronger the pull. This results in the back-and-forth oscillatory movement.
2. What is the defining equation of SHM and what does the negative sign signify? The defining equation of Simple Harmonic Motion is a = -ω²x, where 'a' represents the acceleration of the object, 'x' is its displacement from the equilibrium position, and 'ω' is the angular frequency. The negative sign is crucial because it signifies that the direction of the acceleration is always opposite to the direction of the displacement. If the object is displaced to the right of the equilibrium point, the acceleration will be to the left and vice-versa, always restoring the object back towards the equilibrium.
3. What does the provided resource mean by the term 'equilibrium position'? The equilibrium position in SHM refers to the central, fixed point about which the object oscillates. It is the position where the net force acting on the object is zero, and the object would remain at rest if it were not moving. This position acts as the target that the restoring force always aims to bring the object back to.
4. What is the purpose of the JavaScript HTML5 Applet Simulation Model mentioned in the source? The JavaScript HTML5 Applet Simulation Model, specifically referencing "SHM07", is an interactive tool designed to visually demonstrate and explore the concepts of Simple Harmonic Motion. It allows users to run simulations and manipulate parameters to observe how changes affect the motion of an object exhibiting SHM. This type of model is beneficial for learning because it provides a dynamic and visual way of understanding abstract concepts. It also works on different platforms, including desktops, laptops, and mobile devices.
5. What are some examples of interactive simulations offered by the provided resource besides the SHM model? The source lists numerous interactive simulations beyond just SHM, spanning different scientific and mathematical topics. Some examples include: simulations of various physics concepts like projectile motion, collisions, wave motion, and electromagnetism, models for primary school science like light and shadow or evaporation, simulations for mathematics (e.g., geometry, algebra), and even games for educational purposes across various subjects. These resources utilize the Easy JavaScript Simulation (EJS) framework for building interactive learning tools.
6. How can these interactive simulations be useful for teaching and learning? Interactive simulations provide a hands-on and engaging way for learners to explore complex concepts. They allow students to manipulate variables, observe the direct impact of those changes, and often come to their own conclusions. The dynamic visual nature of the simulations promotes a more intuitive understanding. Furthermore, the accessibility across various platforms makes them versatile for use both inside and outside traditional classroom settings. Additionally, they often provide a way for teachers to show real physics in action, helping abstract concepts feel more concrete.
7. What is WebEJS, and what role does it play in the creation of these simulations? WebEJS (Easy JavaScript Simulation) is an authoring toolkit and framework for creating interactive simulations using JavaScript and HTML5. It is used to develop the simulations in the provided resource. WebEJS is essential for educators and developers looking to create interactive content without needing to be professional programmers. It provides a simplified way to model and visualize science and math concepts that can then be embedded into web pages or other educational platforms.
8. How are these resources licensed and can they be used commercially? The educational content provided is licensed under a Creative Commons Attribution-Share Alike 4.0 Singapore License. This generally means that the materials can be shared, adapted, and used for educational purposes, as long as the original source is credited and the new material is shared under the same terms. However, commercial use of the EasyJavaScriptSimulations Library requires a separate agreement with the library owners as indicated by the link provided in the original text.