About

1.1.3 Introduction to terms used LO (c)

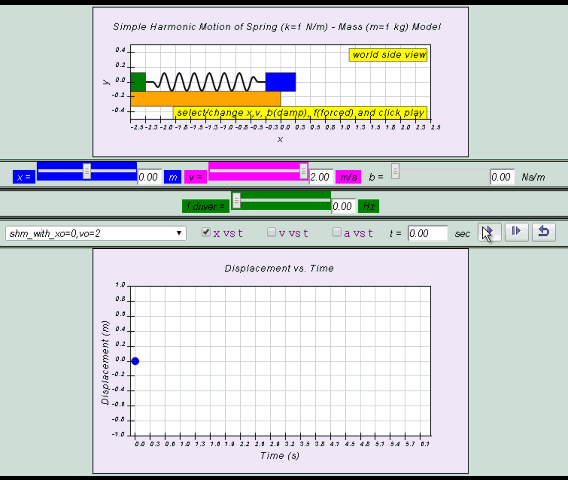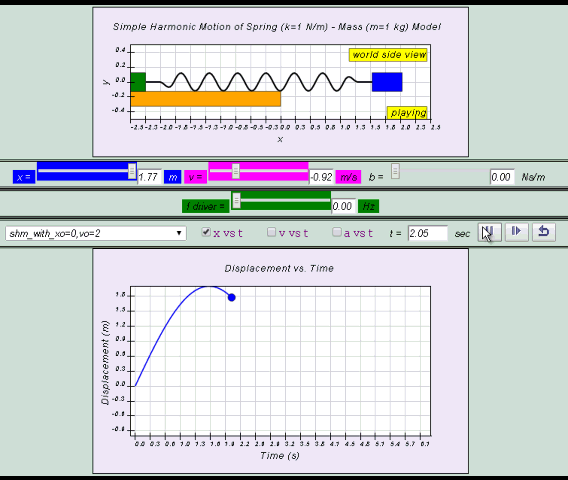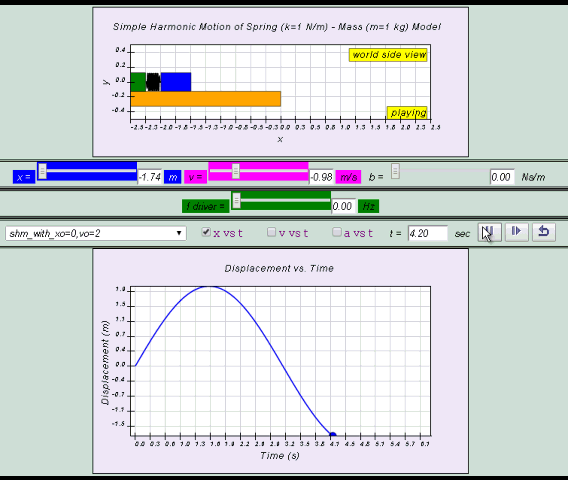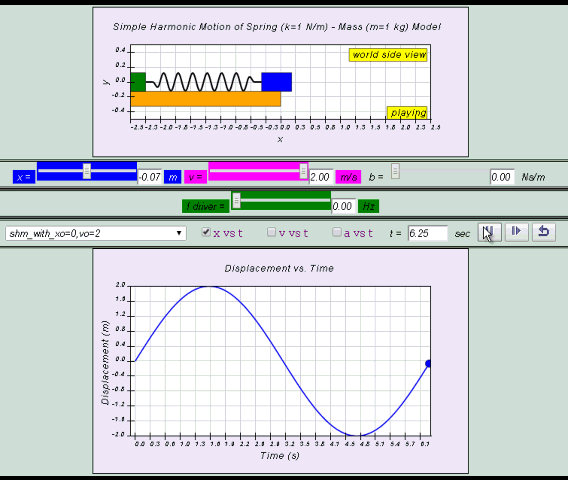
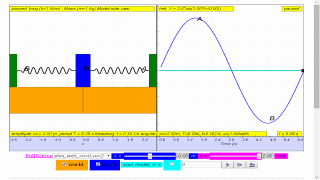
1.1.3.1 Q1: Consider an object P oscillating between point A and B about the origin (0,0), assuming the usual Cartesian Coordinate System apply.  Observe the Model and suggests possible meaning of the following points with the most suitable descriptions.

Central equilibrium position _ B O P A  

Instantaneous position _ B O P A  

Maximum amplitude _ B O P A m

Minimum amplitude _ B O P A m

Given the equation x = x₀ sin ( ω t ) can describe SHM, suggests the usual symbols associated to the physical quantity

Central equilibrium position  _ 0 x x0 -x0 w t T f  

Instantaneous position or displacement given by vector OP  _ 0 x x0 -x0 w t T f m

Maximum amplitude  _ 0 x x0 -x0 w t T f m

Minimum amplitude  _ 0 x x0 -x0 w t T f m

Time taken for one complete oscillation, for example Path from O→A→O→B→O   _ 0 x x0 -x0 w t T f s

Number of oscillations performed per unit time _ 0 x x0 -x0 w t T f 1/s. Hence, f and T are related by the equation ${\displaystyle f=\frac{1}{T}}$

Angular frequency _ 0 x x0 -x0 w t T f rad/s. Since one complete oscillation is 2π radians, ω and f are related by ω = 2π f
 
 

1.1.3.2 Example

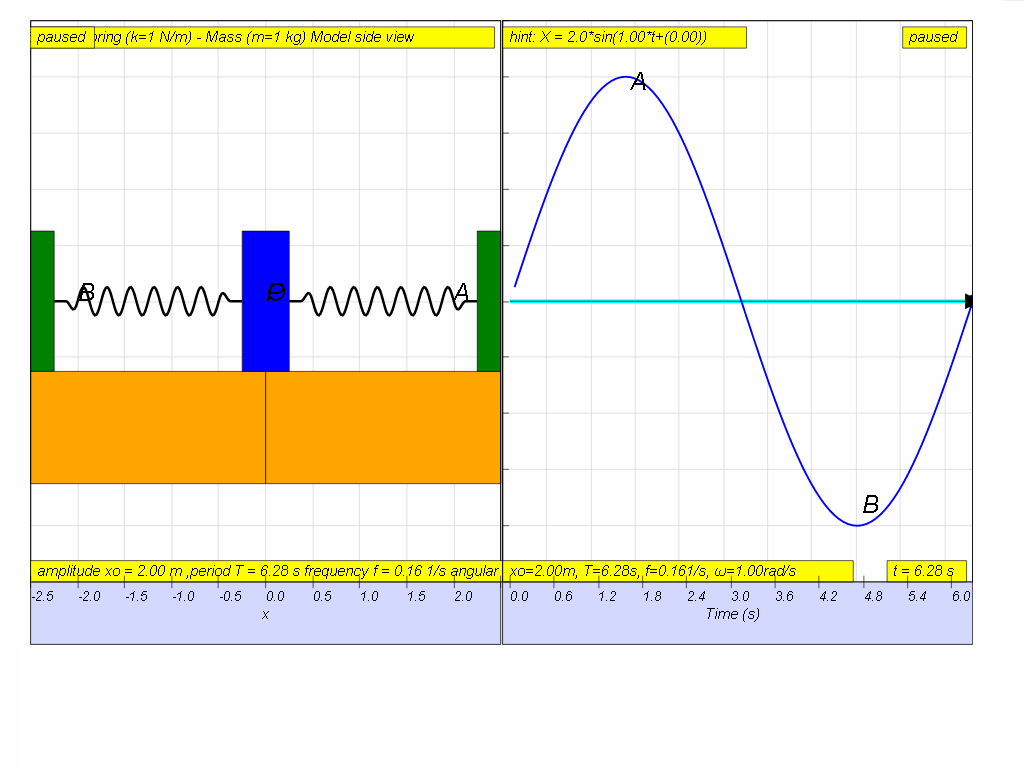
1.1.3.2.1 The displacement of a spring mass system from a fixed point is as shown. From the graph, determine the
(a)     amplitude,  
(b)     period,     
(c)     frequency,      
(d)     angular frequency, of the oscillations.
[2.00 m, 6.28 s, 0.159 Hz, 1.00 rad s^–1]

1.1.3.2.2  Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/69

Suggested Activity Q1: run model with different starting x to explore the meaning of amplitude
Suggested Activity Q2: run model with different mass m and spring constant k to explore different period T, frequency f and angular frequency ω
 

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.; Francisco Esquembre; Flix Jess Garcia Clemente

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM04/SHM04_Simulation.xhtml

{accordionfaq faqid=accordion3 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}

Apps

https://play.google.com/store/apps/details?id=com.ionicframework.shm08app156228&hl=en

Video

https://youtu.be/fHBLMbKi4vA   Progressive mathematical modeling with OSP@SG by lookang lawrence wee

 

 

 

 

 

end faq

{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}