
About
For Teachers
Credits
Author: Tang Yimian video: model lookang
Contact: This email address is being protected from spambots. You need JavaScript enabled to view it.

Document Brief: Pendulum Collision Analysis Using Tracker
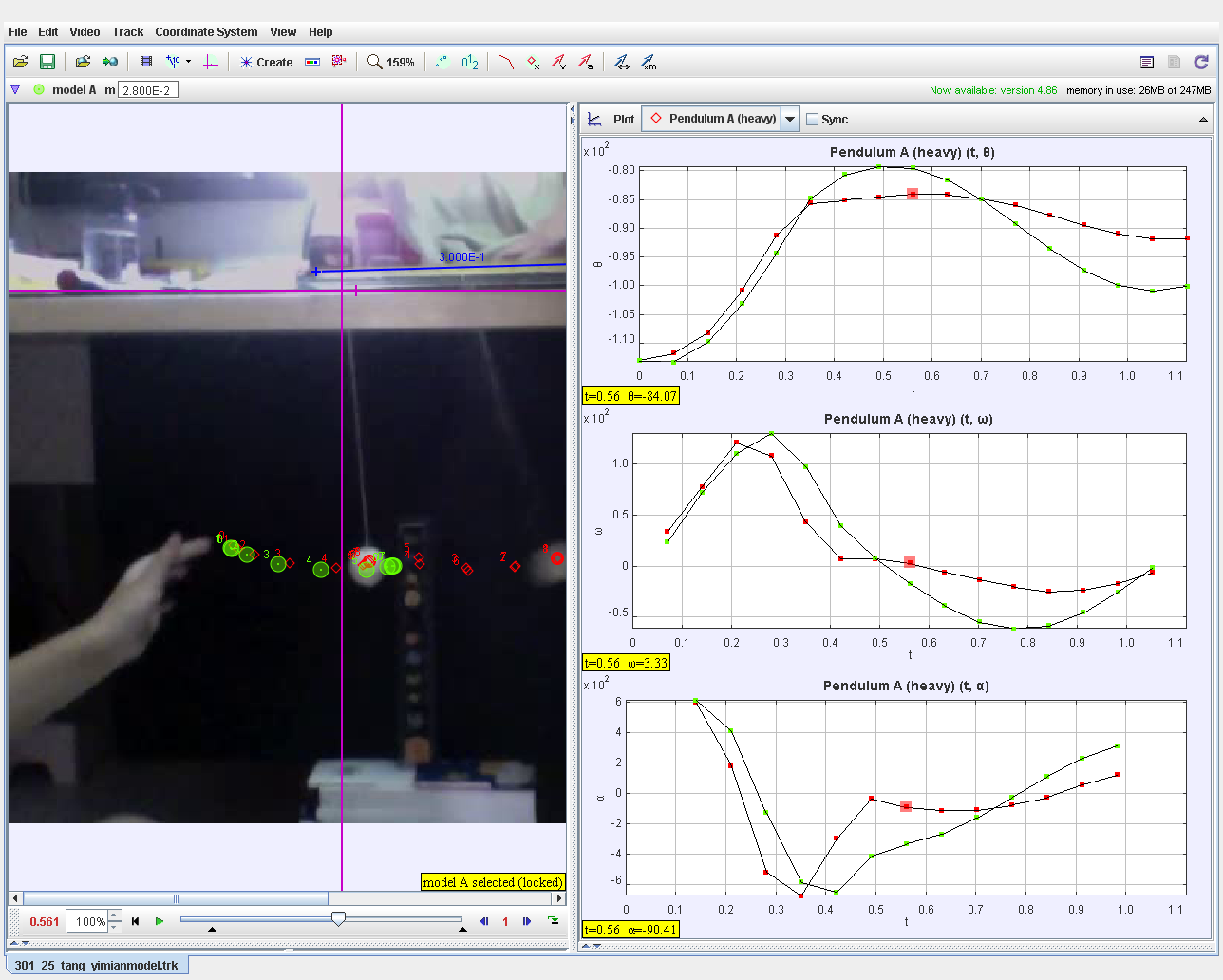
This document explores the dynamics of a pendulum system undergoing a collision, modeled and analyzed using Tracker software. The study focuses on the motion of a heavy pendulum before and after a collision, analyzing its angular displacement (θ), angular velocity (ω), and angular acceleration (α) over time.
Purpose:
To investigate the behavior of a pendulum system during a collision, including the transfer of momentum and energy, and validate experimental observations with theoretical predictions.
Key Features:
- Tracking the motion of the pendulum in polar coordinates (θ,ω,α).
- Analysis of angular displacement, velocity, and acceleration before and after collision.
- Visualization of the collision dynamics using graphical representations.
Study Guide: Modeling Pendulum Collisions
Learning Objectives:
- Understand the conservation of momentum and energy in pendulum collisions.
- Analyze angular displacement, velocity, and acceleration during the collision event.
- Validate theoretical models of collision dynamics against experimental data.
Step-by-Step Guide:
-
Setup and Calibration:
- Import the pendulum collision video into Tracker.
- Calibrate the scale using visible references for accurate measurements.
-
Tracking Motion:
- Track the motion of the pendulum frame by frame.
- Focus on the position, angular displacement (θ\theta), and velocity (ω\omega) at the collision event.
-
Graphical Analysis:
- Plot angular displacement θ vs. time ():
- Observe the change in motion after the collision.
- Analyze angular velocity ω vs. time to identify the momentum transfer during the collision.
- Plot angular acceleration (α\alpha) to study changes in force dynamics.
- Plot angular displacement θ vs. time ():
-
Collision Modeling:
- Apply the equations of motion for the pendulum before and after the collision:
- τ=I⋅α, where τ\tau is torque and is the moment of inertia.
- Conservation of angular momentum: L1=L2, where L=I⋅ωL .
- Estimate the energy transfer and losses during the collision.
- Apply the equations of motion for the pendulum before and after the collision:
-
Applications:
- Study momentum and energy conservation in rotational systems.
- Analyze the effects of collision on oscillatory systems in engineering or physics.
Tips for Success:
- Ensure accurate tracking of the pendulum’s motion during and after the collision.
- Compare theoretical predictions with experimental data for validation.
FAQ: Pendulum Collision Analysis
1. What happens during the pendulum collision?
During the collision, energy and momentum are transferred between the pendulum and the colliding body. The motion changes depending on the collision type (elastic or inelastic).
2. What is conserved during the collision?
- Elastic Collision: Both energy and angular momentum are conserved.
- Inelastic Collision: Only angular momentum is conserved, while some energy is dissipated.
3. How is angular momentum used in the analysis?
Angular momentum L=I⋅ω is used to describe the rotational motion. Before and after the collision, L1=L2 ensures conservation.
4. How can energy losses be calculated?
Energy losses can be estimated by comparing the kinetic energy before and after the collision:
Energy Loss=KEinitial−KEfinal
5. What do the graphs of ω\omega and α\alpha indicate?
- Angular velocity (ω) shows the change in rotational speed.
- Angular acceleration (α) highlights the forces involved during and after the collision.
6. What are the practical applications of this analysis?
- Understanding collision dynamics in physics and engineering.
- Designing systems like pendulum clocks or impact-based mechanisms.
- Studying energy dissipation in rotational systems.
7. Can damping be included in this model?
Yes, damping can be included by adding a term proportional to ω\omega in the torque equation (τ=−b⋅ω).
- Details
- Parent Category: 02 Newtonian Mechanics
- Category: 09 Oscillations
- Hits: 5482
