About

7.3.8.6 Example of Application of potential ϕ

7.3.8.6.1 Revision:

  The total ϕ at a point in a field due to two or more source masses is the scalar addition of the individual ϕ due to each mass at that point, i.e.  .
ϕ_total = ∑ϕ

Similarly, since PE = U = mϕ

PE _total = $m\sum \varphi$

Showing how the gravitational potential varies between the surface of the Moon and the surface of the Earth along the line joining the centres.

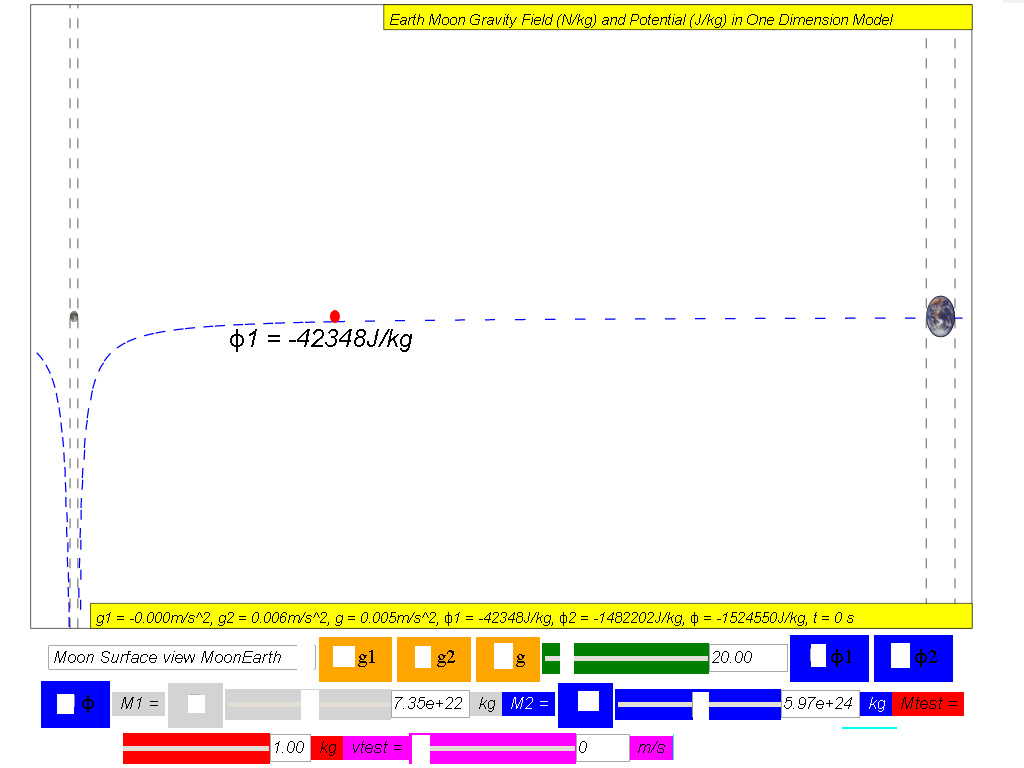
ϕ₁ = Gravitational potential due to Moon

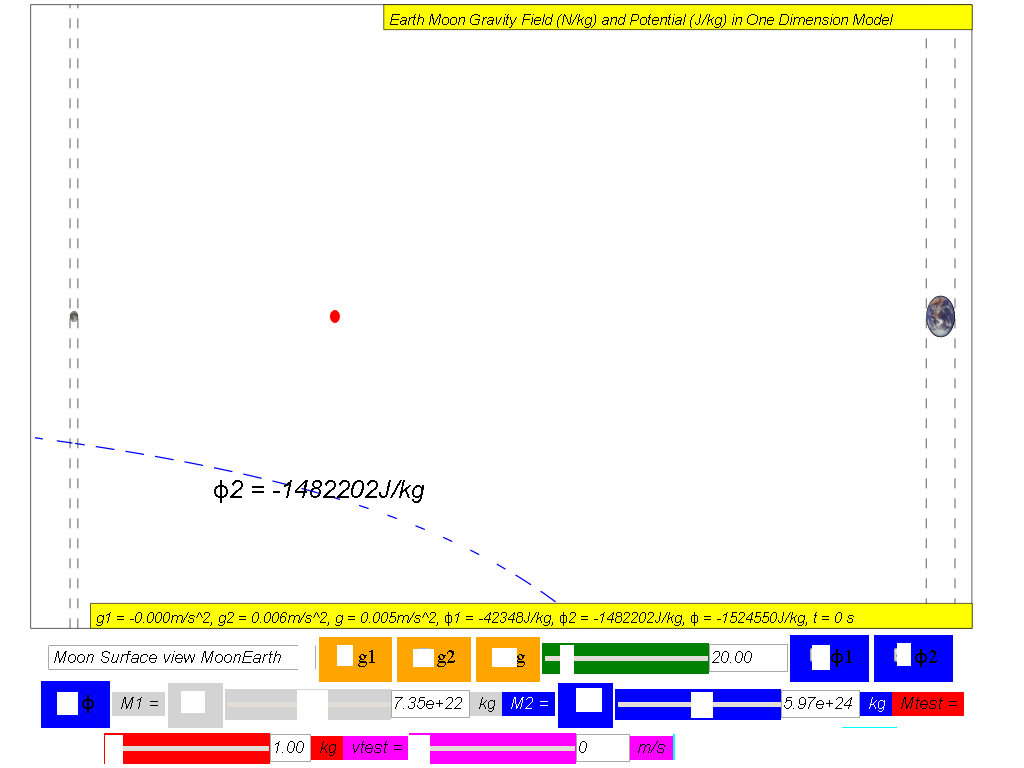ϕ₂ = Gravitational potential due to Earth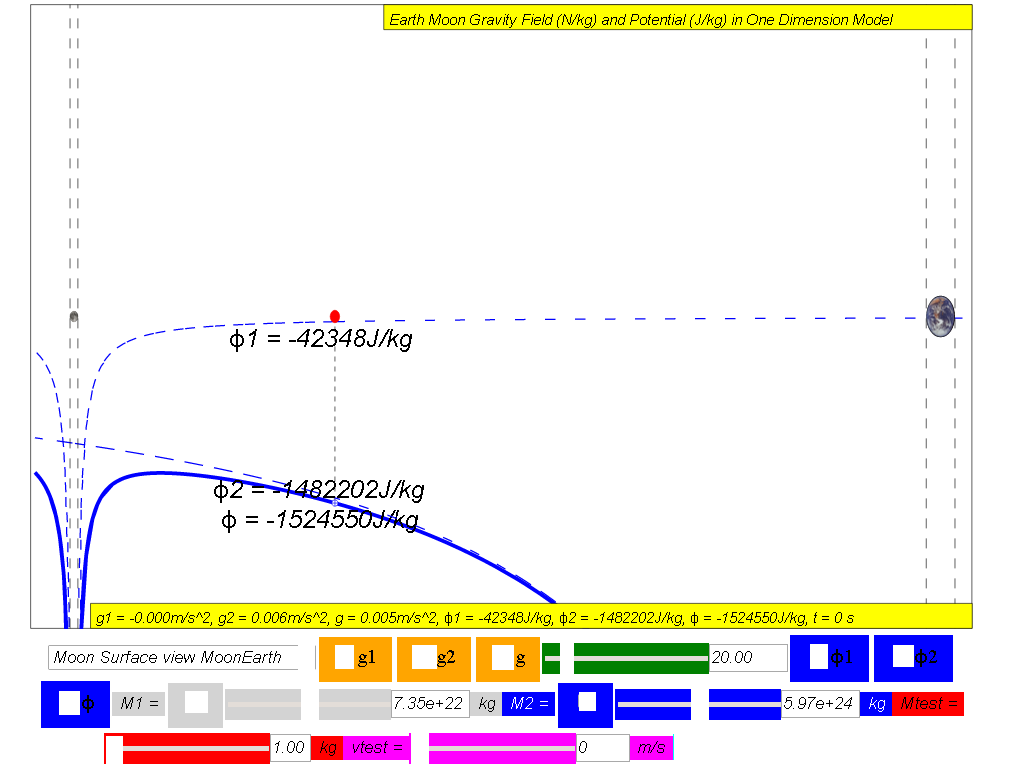



ϕ_total = ϕ₁ +ϕ₂ = Net gravitational potential along the line of centres is equal to the sum of the gravitational potentials due to the Earth and Moon

7.3.8.6.2 Escape Speed Is it true that 'what goes up must come down'? 

It is only accurate to say that 'what goes up may come down'.  There is a critical speed at which an object can be launched such that it can escape the Earth permanently.  Such a critical speed is termed as the escape speed.

7.3.8.6.2.1 Example Determine an expression for the escape speed, v, of a rocket of mass m launched from the surface of Earth of mass M and radius R.

By conservation of energy, assuming at r = ∞, the minimum speed is 0.

KE_{earth surface} + PE_{earth surface} = KE_∞ + PE_∞

$\genfrac{}{}{0.1ex}{}{1}{2}m{v}^2+\left(\genfrac{}{}{0.1ex}{}{-GmM}{r_{earth}}\right)=0+0$

$\genfrac{}{}{0.1ex}{}{1}{2}{v}^2+\left(\genfrac{}{}{0.1ex}{}{-\left(6.67x10^{-11}\right)\left(6.0x10^{24}\right)}{6.37x10^6}\right)=0+0$

v = 1.12x10⁴ m/s

Therefore, to escape from Earth, it implies that the projectile must have a minimum launch velocity of v = 1.12x10⁴ m/s .





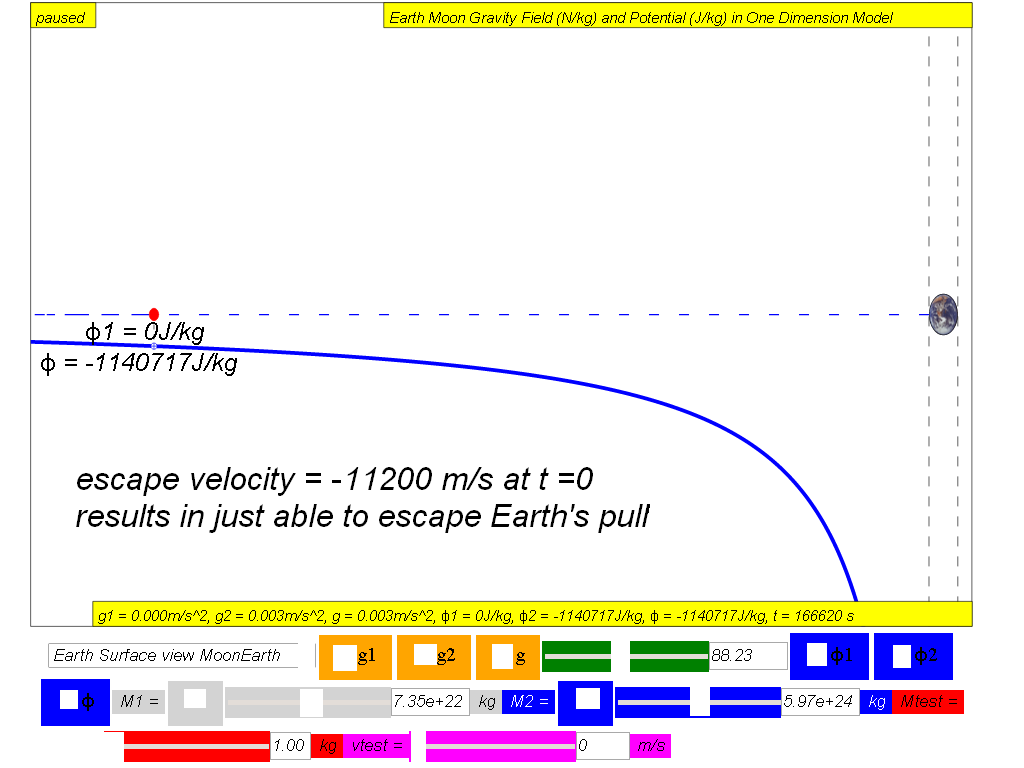
To understand the escape velocity concept, the following steps could be used as an inquiry approach to experience escape velocity in the context of the simulation.

1. Un-check the M1 moon to remove the effects of the Moon
2. Select from the drop-box menu the option Earth Surface view MoonEarth (Left to Right), and notice the test mass (red) is placed on the surface of the Earth on the right side.
3. Key in on the vtest, velocity of the test mass (magenta) say -10000 m/s (negative as the velocity points to the left of the Cartesian coordinate system)), and click play to observe the effects of launching a projectile at this speed. You could record your observation as "unable to escape from Earth's gravity pull.

Similarly, design an experiment to discover the minimum theoretical speed to escape from Earth's pull.

Can you conclude that any velocity lesser than v = 1.12x10⁴ m/s cannot allow the projectile to escape from Earth's pull?

Can you conclude that any velocity greater than v_{escape Earth} = 1.12x10⁴ m/s allow the projectile to escape from Earth's pull?


Similarly,  you can derive the theoretical escape velocity from Earth's Moon surface and test it on the simulation.
Answer: v_{escape Moon}=2400 m/s


Given that root-mean-square speed is the measure of the speed of particles in a gas that is most convenient for problem solving within the kinetic theory of gases,  is given by $v_{rms}=\sqrt{(}\genfrac{}{}{0.1ex}{}{3RT}{Mm})$

Given molar gas constant R = 8.31 J K⁻¹ mol⁻¹, molar mass of water is Mm H₂0 = 18x10^-3 kg/mol , T is temperature in Kelvin, using the minimum theoretical speed from Moon, suggest the surface temperature of Moon at some point in its history which resulted in the Moon's surface not having water now.

T = 4.2x10³ K

With this limited information, this data seems to suggest at some point of Moon's history, it could have been very hot (T = 4.2x10³ K) which causes water molecules to escape then. As the Moon cools, not enough water molecules was able to form on the Moon's surface to form oceans like what we have on Earth.

7.3.8.6.3 Model ϕ

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/63

 

Translations

Code	Language		Translator	Run

Credits

lookang (This email address is being protected from spambots. You need JavaScript enabled to view it.); andrew duffy

http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejss_model_gravity11/gravity11_Simulation.xhtml 

Versions:

1. http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejs/ejs_model_GFieldandPotential1Dv7EarthMoon.jar by Todd TimberLake and lookang Java version

Other resources

https://www.geogebra.org/m/va3dbqyd by Seng kwang

Writeup ICT

Virtual Laboratory Gravitational Field & Potential of Earth and Moon

Resources

  https://www.geogebra.org/m/va3dbqyd by Tan Seng Kwang

end faq

{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}