About

7.2 Gravitational Field Strength (symbol: g and units: N kg^-1 or m s^-2)

As seen in earlier section, the gravitational field strength acting at a point in the field (previously depicted as M₂ = 1kg) decreases (illustrated by an increase in the field line spacing) as the point moves further away from Earth. This means that field strength varies with distance from the source mass (in this case, the Earth).

The gravitational field strength, g at a particular point in free space is defined as the gravitational force per unit mass acting on a point mass placed at that point.

7.2.1 Why point mass assumption:

Why must it be a 'point mass'?
To simplify analysis, point mass are used as they are physically very small so that the point mass itself does not distort the gravity field of its surrounding. Another reason could be that the forces acting on different parts of the point mass are generally the same.

7.2.2 g LO(C)

7.2.2.1 Equation

Based on Newton’s law of gravitation, the gravitational force acting on the point mass, m by the source mass, M, (notice M₁ is denoted by M and M₂ is denoted by m respectively)$$

$F=\frac{G{M}_1{M}_2}{r^2}$   

$F=\genfrac{}{}{0.1ex}{}{GMm}{r^2}$ ---------------------------------------------------------- (1)

and gravitational field strength, g is the gravitational force, F per unit mass acting on the point mass, m, we may derive the gravitational field strength.

Since we know the force on object as a result of the gravitational field created by Earth is 

F = mg  --------------------------------------------------------- (2)

putting the equations (1) and (2) together, we get  
$$    

$F=mg=m\genfrac{}{}{0.1ex}{}{GM}{r^2}$

giving us the expression for gravitational field field g

$g=\genfrac{}{}{0.1ex}{}{GM}{r^2}$

7.2.2.2 Graphical representation

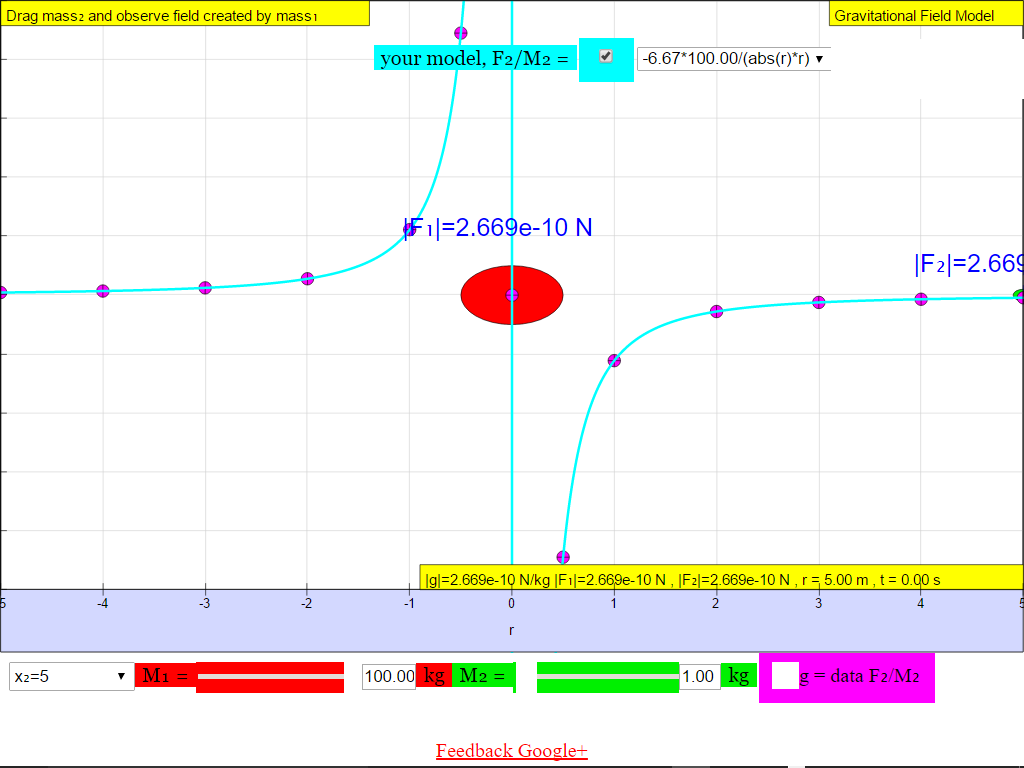
The following shows the different g field strength at different positions away from the mass M creating the gravitational field.
From left to right, for the case when M = 100 kg.

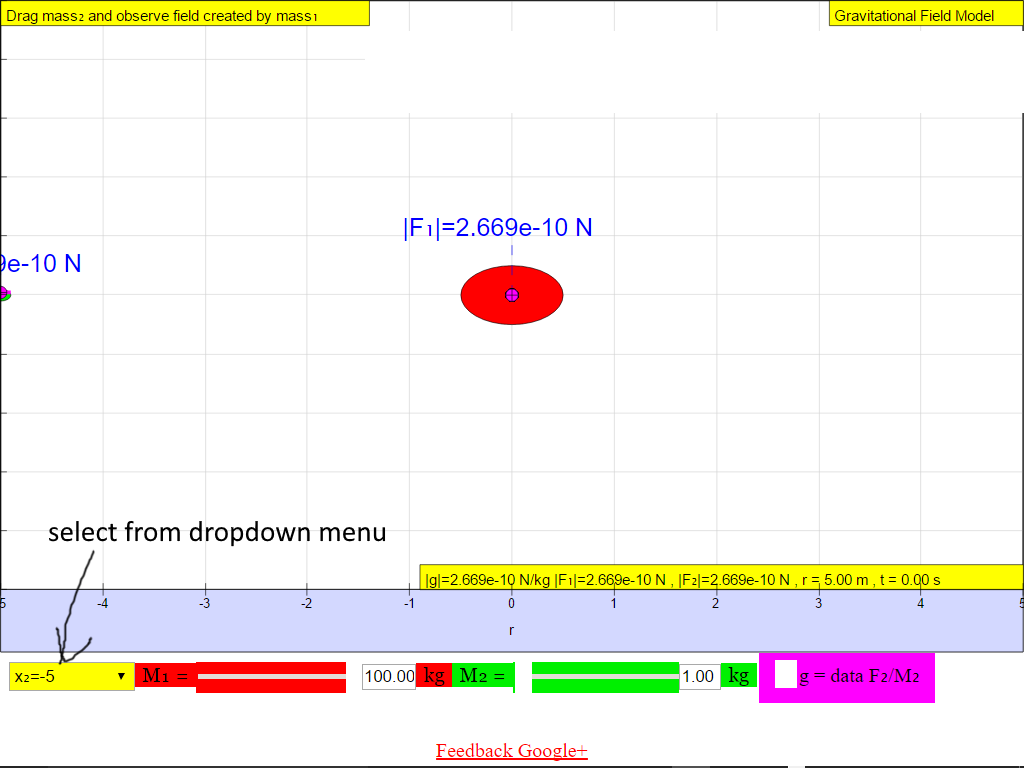
When r = -5.0 m, |g| = 2.669x10^-10 N/kg towards M

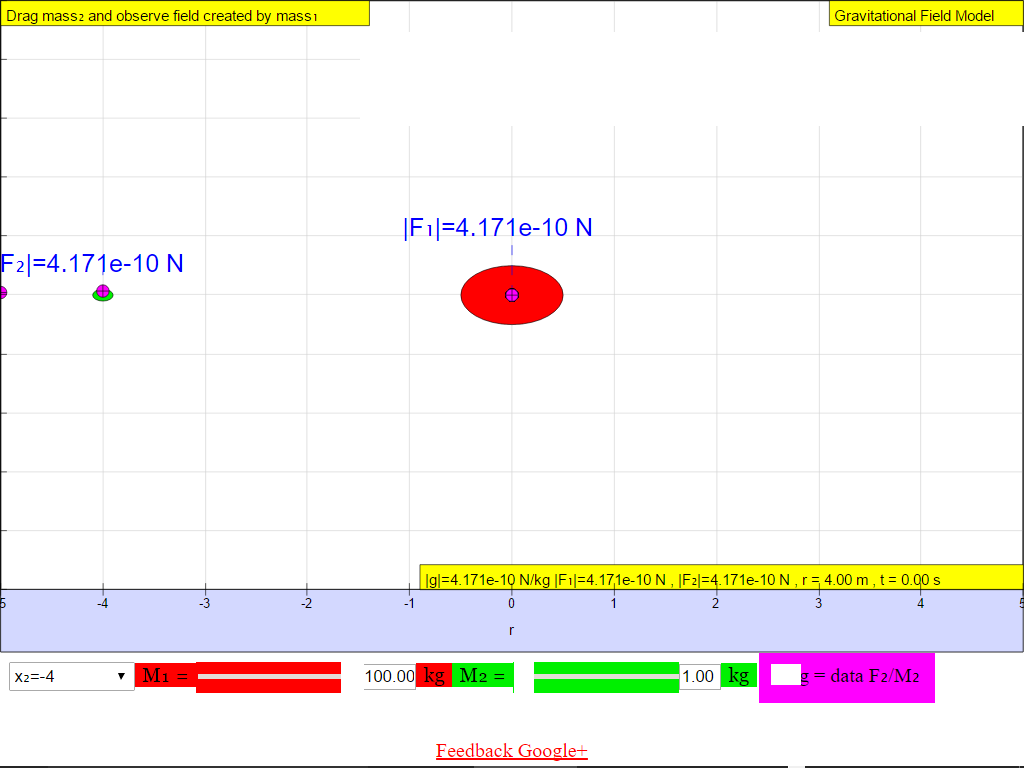
When r = -4.0 m, |g| = 4.171x10^-10 N/kg towards M

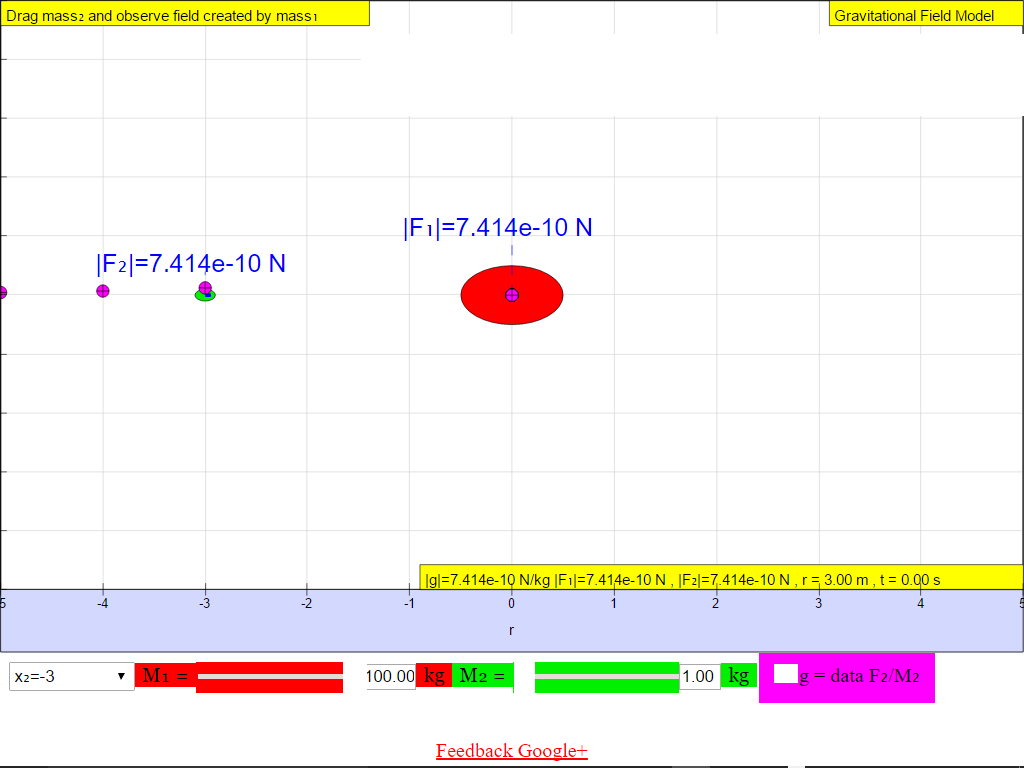
When r = -3.0 m, |g| = 7.414x10^-10 N/kg towards M

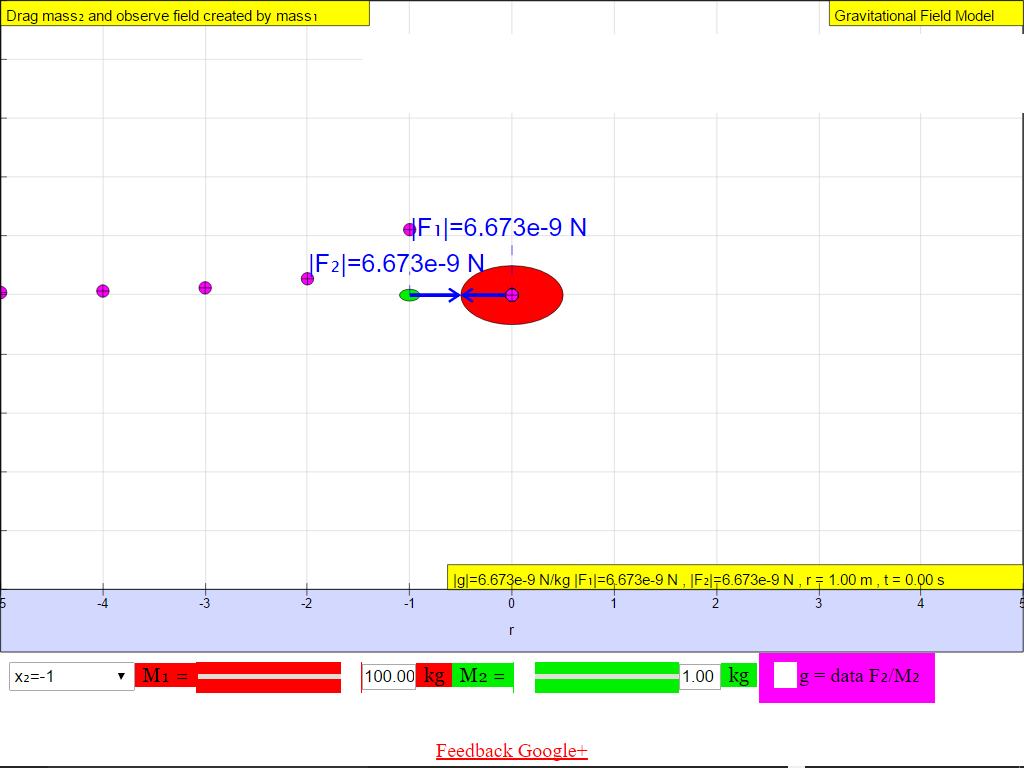
When r = -2.0 m, |g| = 1.672x10^-10 N/kg towards M

When r = -1.0 m, |g| = 6.673x10^-9 N/kg towards M






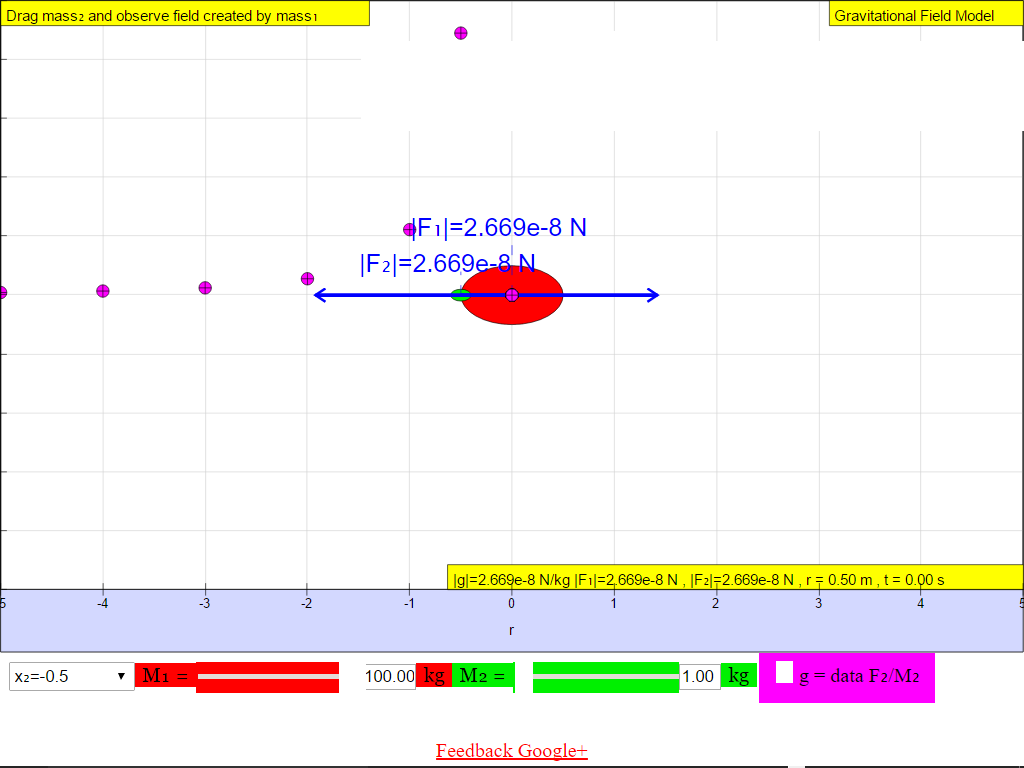
When r = -0.5 m, |g| = 2.669x10^-8 N/kg towards M




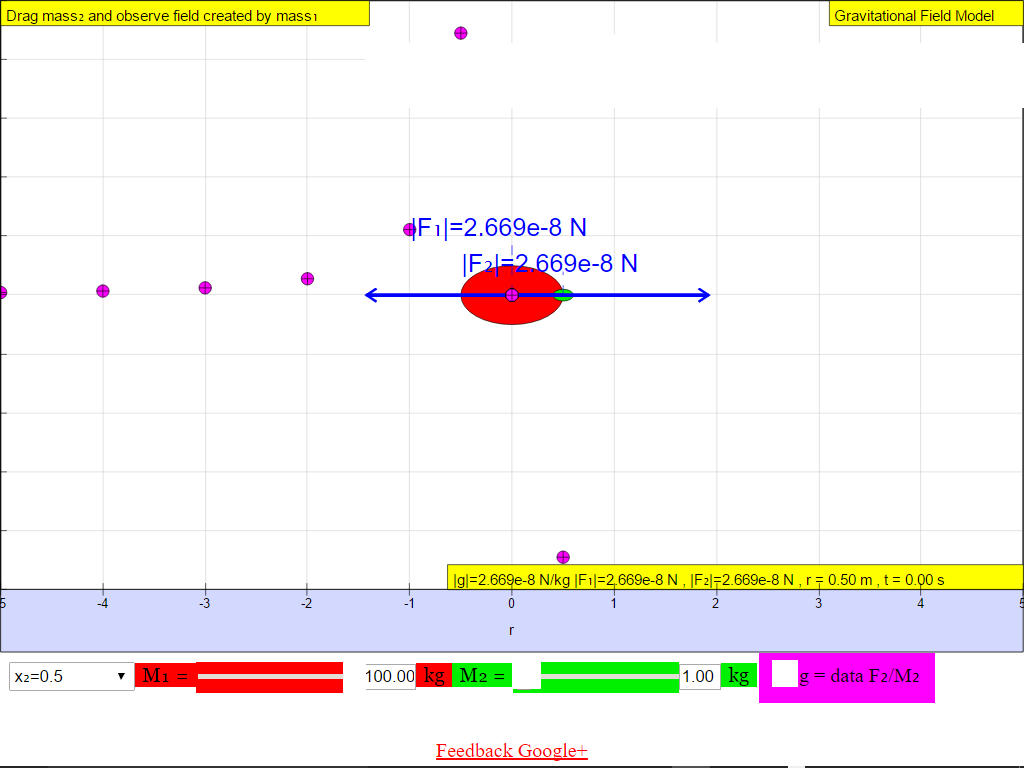
When r = +0.5 m, |g| = 2.669x10^-8 N/kg towards M


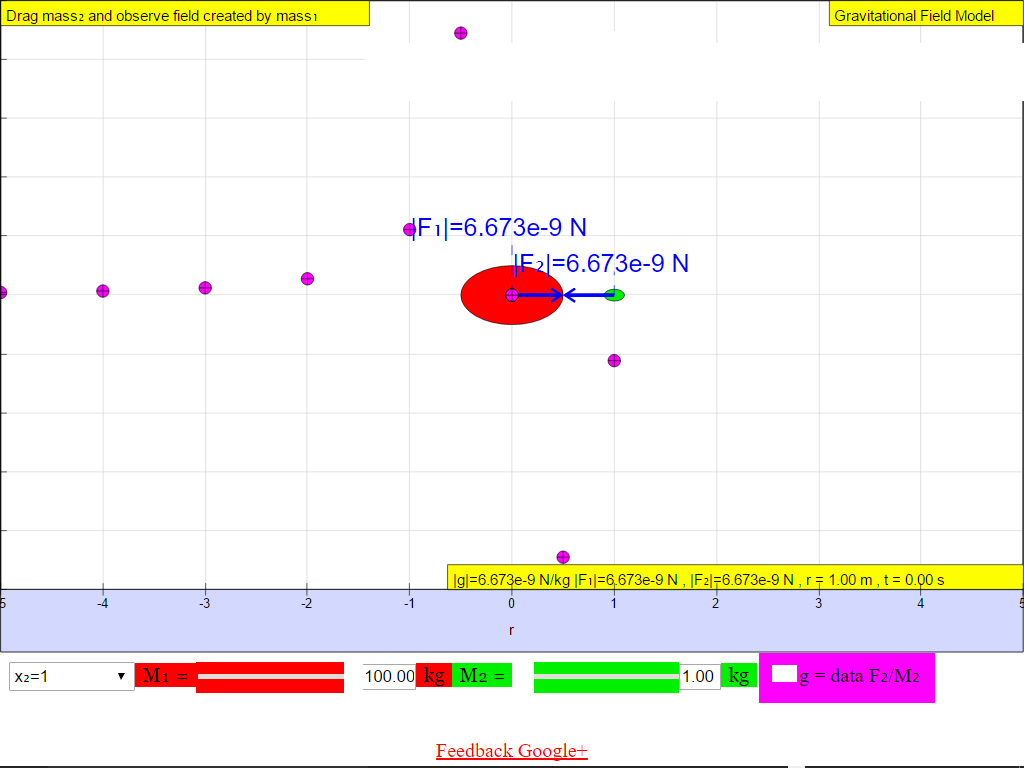
When r = 1.0 m, |g| = 6.673x10^-9 N/kg towards M


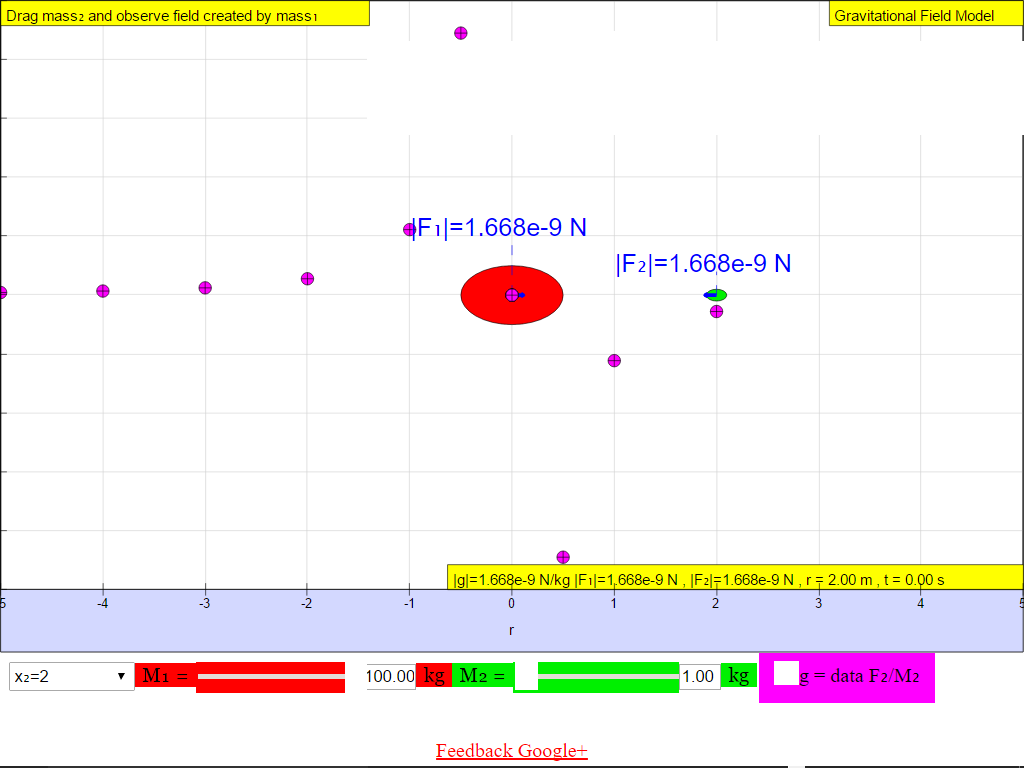
When r = 2.0 m, |g| = 1.668x10^-9 N/kg towards M

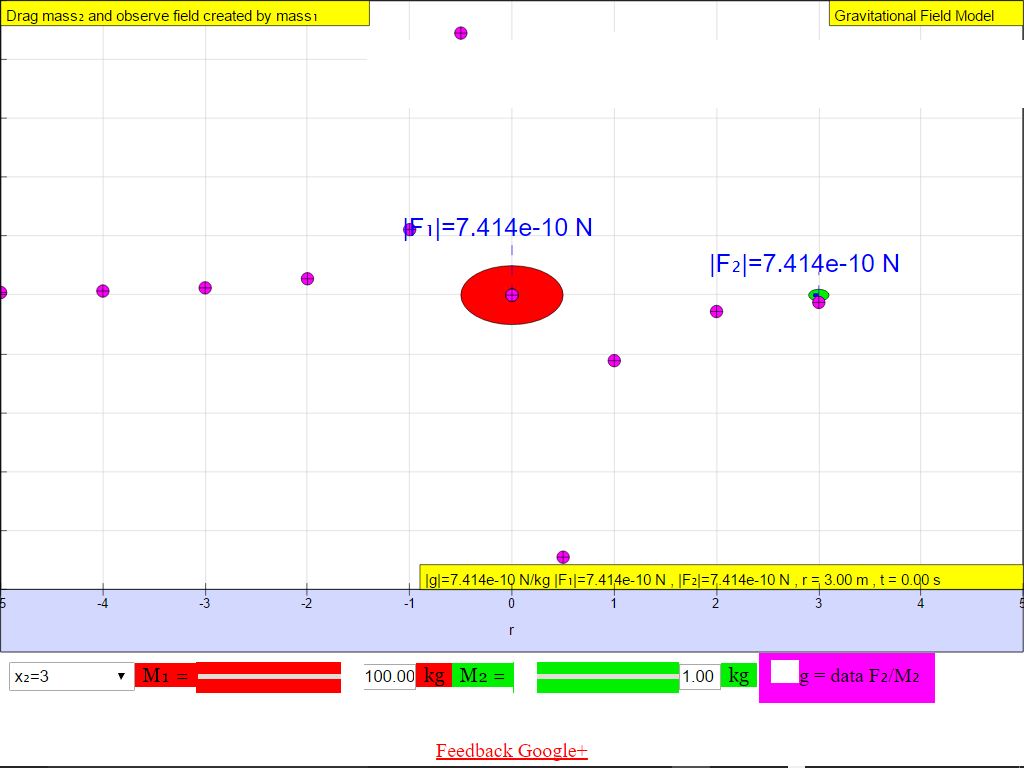
When r = +3.0 m, |g| = 7.414x10^-10 N/kg towards M


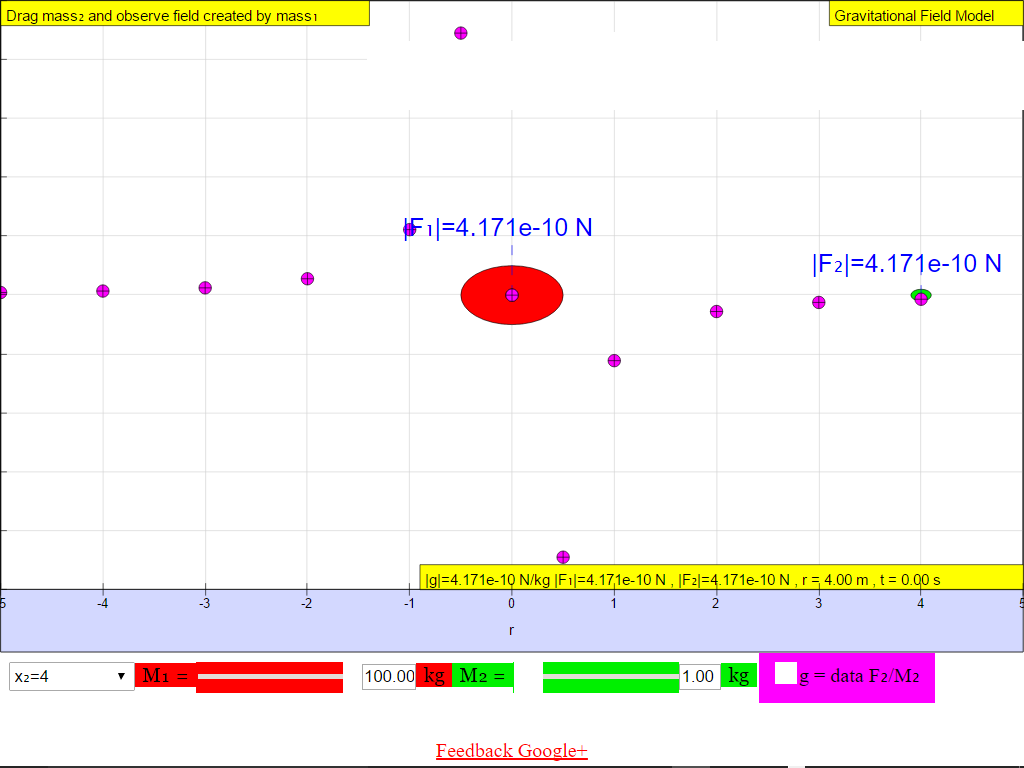
When r = +4.0 m, |g| = 4.171x10^-10 N/kg towards M


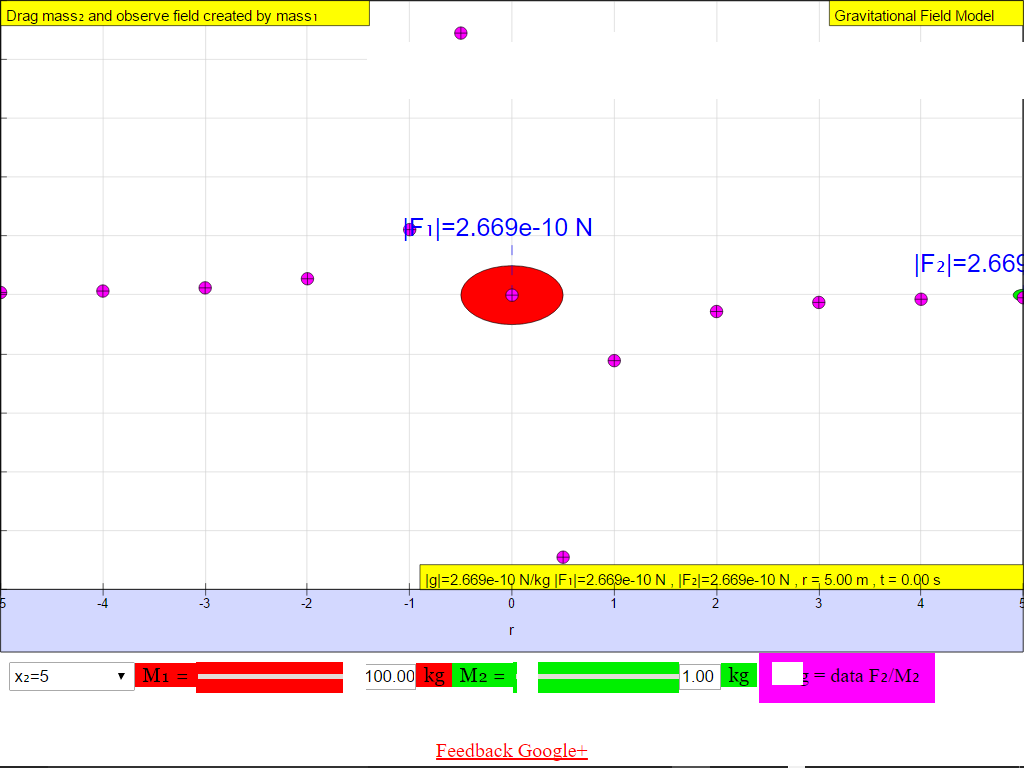
When r = 5.0 m, |g| = 2.669x10^-10 N/kg towards M.

7.2.2.3 Vector Quantity

Suggest whether g field is a vector (possessing both magnitude and direction) or scalar (possessing only magnitude, no direction) quantity.

1)    Gravitational field strength, g (depicted as a magenta color curve) is a vector quantity, and it has a direction which is always towards the mass M.

7.2.2.4 Independent of test mass m

Try varying the values of the green test mass m, does it change the value of g due to mass M alone?

  As shown in  $g=\genfrac{}{}{0.1ex}{}{GM}{r^2}$, the gravitational field strength of source mass M , g is independent of the mass at that point, m. 

7.2.2.5 Modeling activity with Simulation.

From the pictures above, how do the values of g changes with r?
Is the relationship linear, quadratic, inverse square etc?
Try your own model by keying an expression to test  linear = "r", quadratic = "r^2", inverse square = "1/r^2".
Which model seems to "fit" the g well?
The suggested activities is on 7.2.6 Model can you think of a mathematically valid equation to represent the gravitational field strength, g ?

7.2.2.5.1 gravitational field inverse square law field

  The magnitude of the field strength , g varies according to the inverse square law  $gproportional\frac{1}{r^2}$ .Hence gravitational field is also known as an inverse square law field. In other words as r increases, magnitude of g decreases according the formula $g=\frac{GM}{r^2}$

7.2.2.5.2 gravitational field points towards source mass M

•    On the left side of the M =100-kg mass, the gravitational field strength points to the right are positive values.
•    On the right side of the M =100-kg mass, the gravitational field strength points to the left are negative values.
The reason is because of the adoption of the Cartesian coordinate system with positive x direction to the right.

Activity to do

Complete section (A) & (B) in ICT inquiry worksheet 1 using the EJS below to build your conceptual understanding on gravitational field strength. The HTML5 version is below, the Java worksheet customization to HTML5 is work in progress.

7.2.3 YouTube

https://youtu.be/nZSHpQmlddk video tutorial to explain how to use the simulations for learning the concepts

7.2.4 Inquiry:

An astronaut feels that he is ‘floating’ in a spacecraft in outer space as the spacecraft rotates around the Earth at a distance of 4 x 10⁷ m from the centre of Earth. He concludes that he is ‘floating’ because he is not experiencing any gravitational field of the Earth. Suggest whether his conclusion is right.

7.2.5 YouTube 

https://youtu.be/_ikouWcXhd0 Resource Running in Space! by ReelNASA

7.2.6 Model:

The following suggested activity is recommended to allow students to use mathematical equations or use the model field to propose a mathematically valid equation to represent the gravitational field strength, g.
Hint: try typing in expression like  6.67*100/r^2 (left)  and - 6.67*100/r^2 (right) separately.
Note that students do not need to key in x10^-11.
Note that the model field assumes G = 6.67 instead of 6.67x10^-11,M = 100 kg, r is the distance away from M (red gravitational field source mass)

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/52

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.; Anne Cox; Wolfgang Christian; Francisco Esquembre

http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejss_model_gravity04/gravity04_Simulation.xhtml

 Apps

https://play.google.com/store/apps/details?id=com.ionicframework.gravity04app388924&hl=en

end faq

{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}