About

7.4.3 Energy of a Satellite in circular orbit in terms of distance from Earth, r

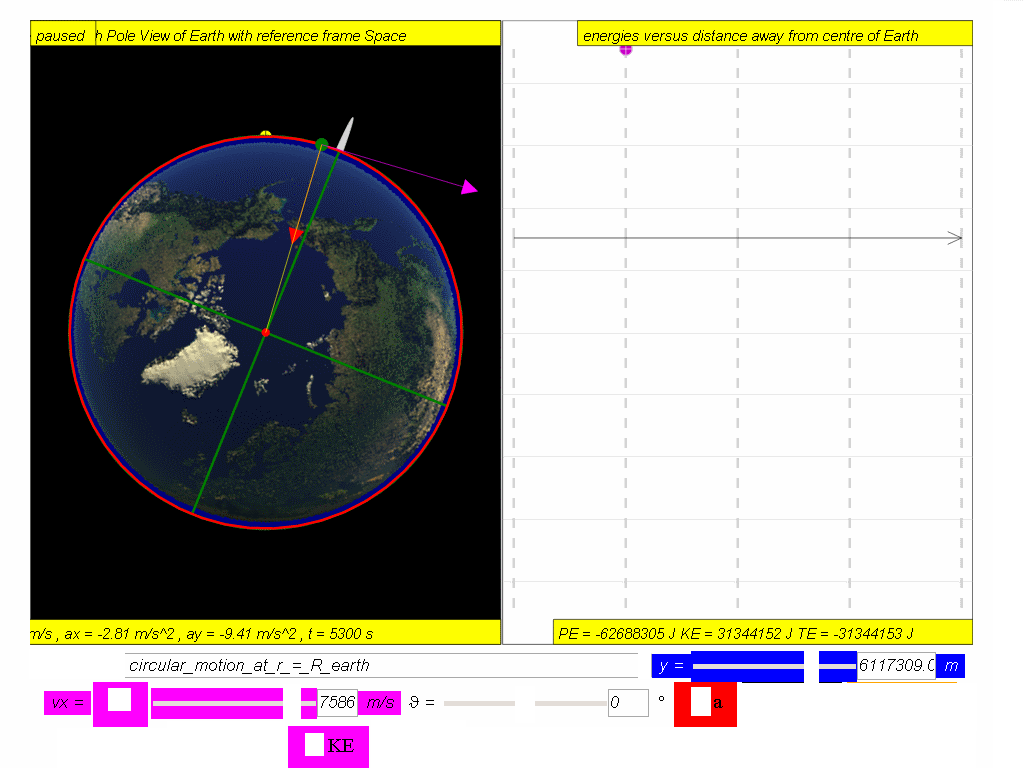
A satellite in orbit possesses kinetic energy, KE, (by virtue of its speed motion) and

gravitational potential energy, PE, (by virtue of its position within the Earth’s gravitational field).

Hence, total energy of a satellite,

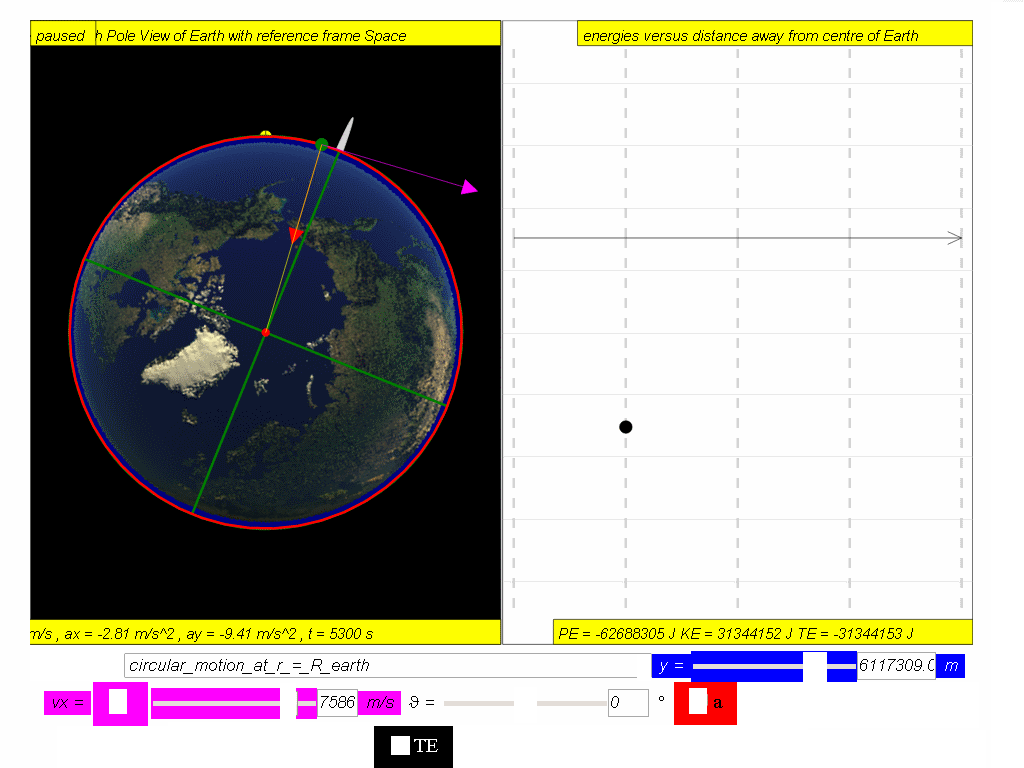
TE = PE + KE
 

   $TE=\left(m\right)(-\genfrac{}{}{0.1ex}{}{GM}{r})+\genfrac{}{}{0.1ex}{}{1}{2}m{v}^2$   --- Equation (1)

Recall that for a satellite in circular orbit, its gravitational force $F=\frac{G{M}_1{M}_2}{r^2}$ acts as the centripetal force:
    ΣF =  ma

$\genfrac{}{}{0.1ex}{}{GmM}{r^2}=\frac{m{v}^2}{r}$

simplifying and multiply by 

$\frac{GmM}{2r}=\frac{1}{2}m{v}^2=KE$--- Equation (2)


Substituting equation (2) into (1),
Hence total energy of a satellite, TE = PE + KE
   

$TE=\left(m\right)(-\genfrac{}{}{0.1ex}{}{GM}{r})+\genfrac{}{}{0.1ex}{}{GmM}{2r}=-\genfrac{}{}{0.1ex}{}{GmM}{2r}$

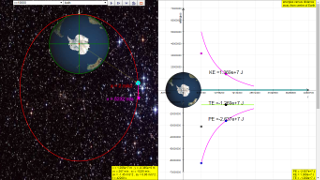
A typical graph showing the relationship between PE, KE and TE with respect to the distance, r, from centre of Earth, O, is as shown.

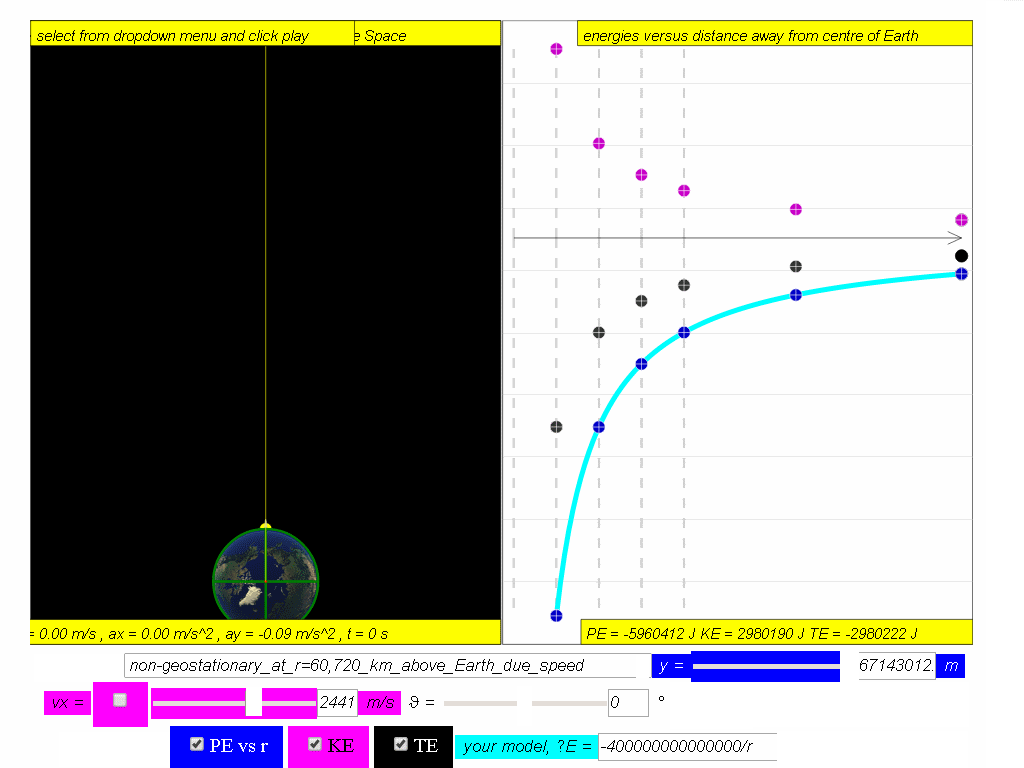
Assuming mass of object m_object = 1kg,  Mass of Earth M_earth = 6.0x10²⁴ kg, G =6.67x10^-11 N m² kg^-2 , The potential energy PE = $PE=-\genfrac{}{}{0.1ex}{}{GmM}{r}=\genfrac{}{}{0.1ex}{}{6.67x10^{-11}\left(1\right)\left(6.0x10^{24}\right)}{r}=-\genfrac{}{}{0.1ex}{}{4x10^{14}}{r}$

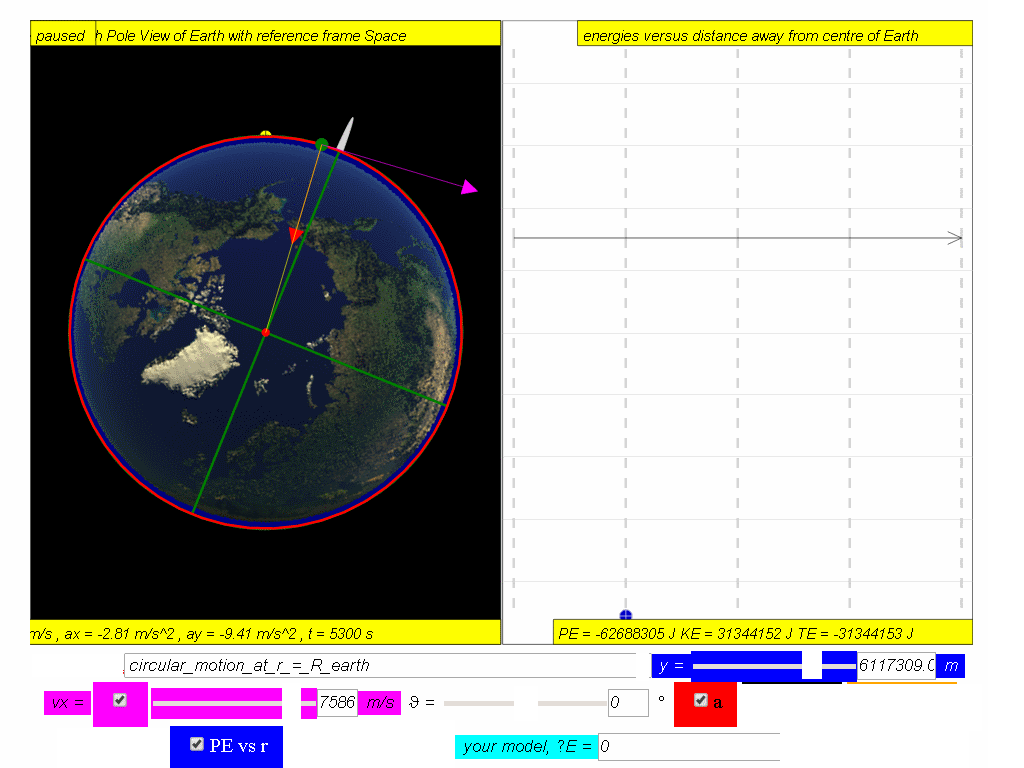
Similarly, determine the equation/model that describes KE and TE and key them into the simulation to test your understanding

$$

$KE=\genfrac{}{}{0.1ex}{}{GmM}{2r}=\genfrac{}{}{0.1ex}{}{6.67x10^{-11}\left(1\right)\left(6.0x10^{24}\right)}{2r}=\genfrac{}{}{0.1ex}{}{4x10^{14}}{2*r}$

$TE=-\genfrac{}{}{0.1ex}{}{GmM}{2r}=-\genfrac{}{}{0.1ex}{}{6.67x10^{-11}\left(1\right)\left(6.0x10^{24}\right)}{2r}=-\genfrac{}{}{0.1ex}{}{4x10^{14}}{2*r}$

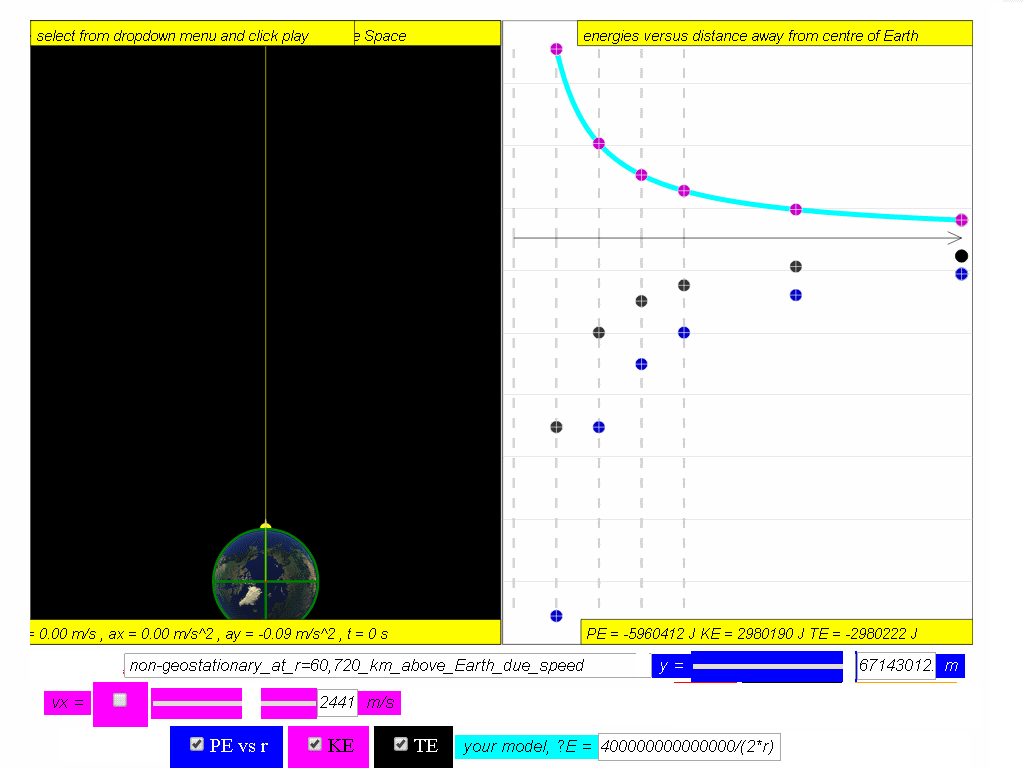
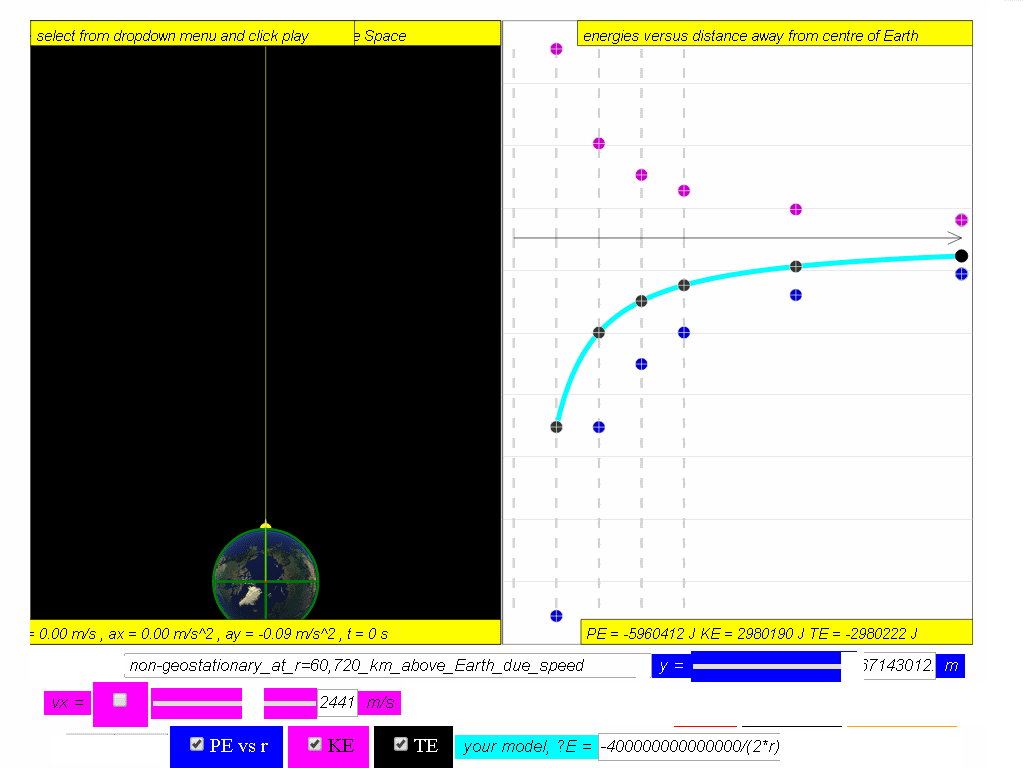
7.4.3.1 Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/285

 

Translations

Code	Language		Translator	Run

Credits

Todd Timberlake, this remixed version is by lookang (This email address is being protected from spambots. You need JavaScript enabled to view it.); lookang; fu-kwun hwang

http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejss_model_gravity08_1/gravity08_1_Simulation.xhtml

App

https://play.google.com/store/apps/details?id=com.ionicframework.gravity081app859103

 Versions

1. http://physics.weber.edu/schroeder/software/NewtonsCannon.html
2. http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejs/ejs_model_NewtonsMountainwee06.jar

 Other Resources

1. http://physics.weber.edu/schroeder/software/NewtonsCannon.html
2. https://scratch.mit.edu/projects/898903/  Launch Simulator by Sushiboy6
3. https://www.geogebra.org/m/jmqytcsc by Tan Seng Kwang

end faq

{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}