7.5 Kepler's Solar System JavaScript HTML5 WebGL Applet Simulation Model

Breadcrumbs

About

gravity09

7.5 Kepler’s Third Law

7.5.1 Newton's Second Law in Circular Motion to derive Kepler’s Third Law T² α r³

By analysing the free body diagram of a satellite in circular orbit, the equation for Newton's Second Law is,

i.e.              ΣF = mrω²
            $\frac{G m M}{r^{2}} = m r ω^{2}$

Recalling in circular motion angular velocity and its period are related as follow, $ω = \frac{2 π}{T}$
Hence,      $\frac{G m M}{r^{2}} = m r ω^{2} = m r {(\frac{2 π}{T})}^{2}$

Which can be simplified to an equation involving T and r

$T^{2} = \frac{4 π^{2}}{G M} r^{3}$

This is the Kepler’s Third Law, which states that the square of the period of an object in circular orbit is directly proportional to the cube of the radius of its orbit. T² α r³

7.5.1.1 Note:

The Kepler’s Third Law T² α r³is only applicable to masses in circular orbit, whereby the gravitational force is the only force acting on it and thus it acts as the centripetal force.

7.5.1.2 Activity

Complete ICT inquiry worksheet 2 to build your conceptual understanding on Kepler’s Third Law.

7.5.1.3 Steps to support your inquiry

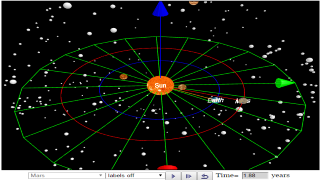
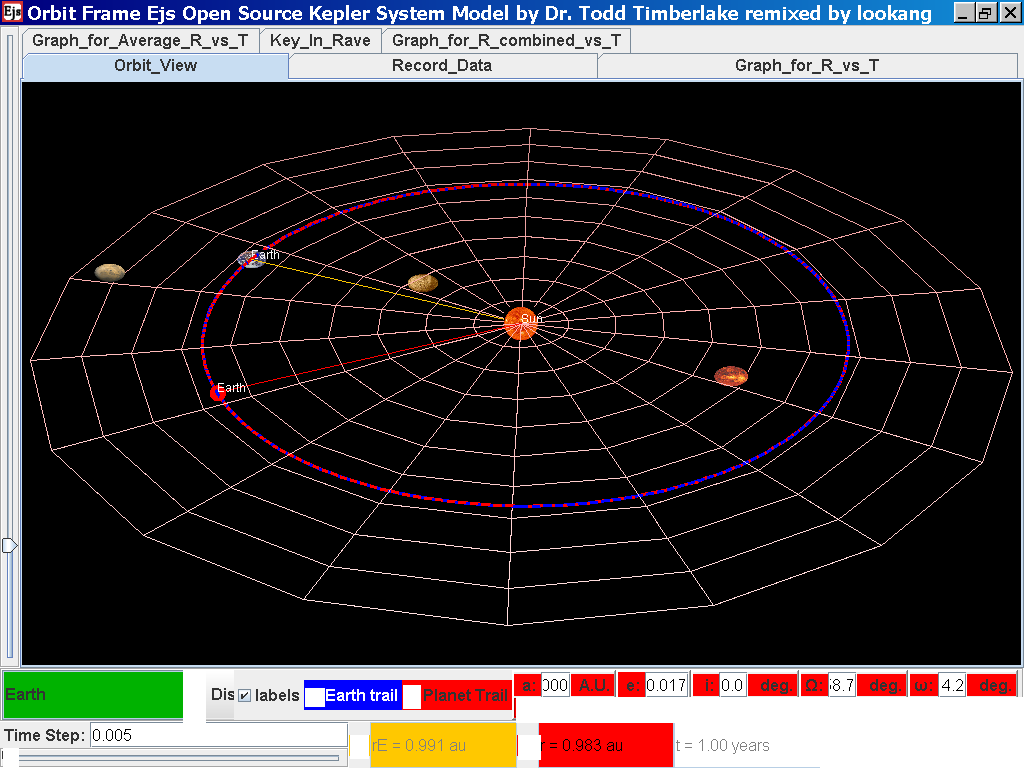
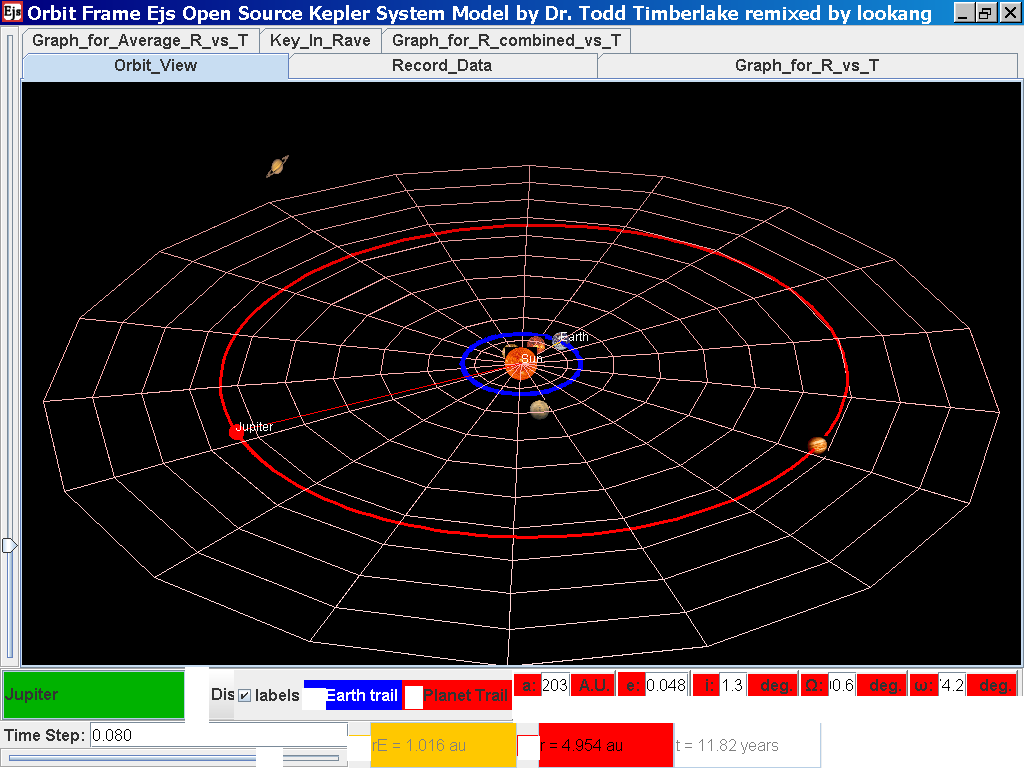
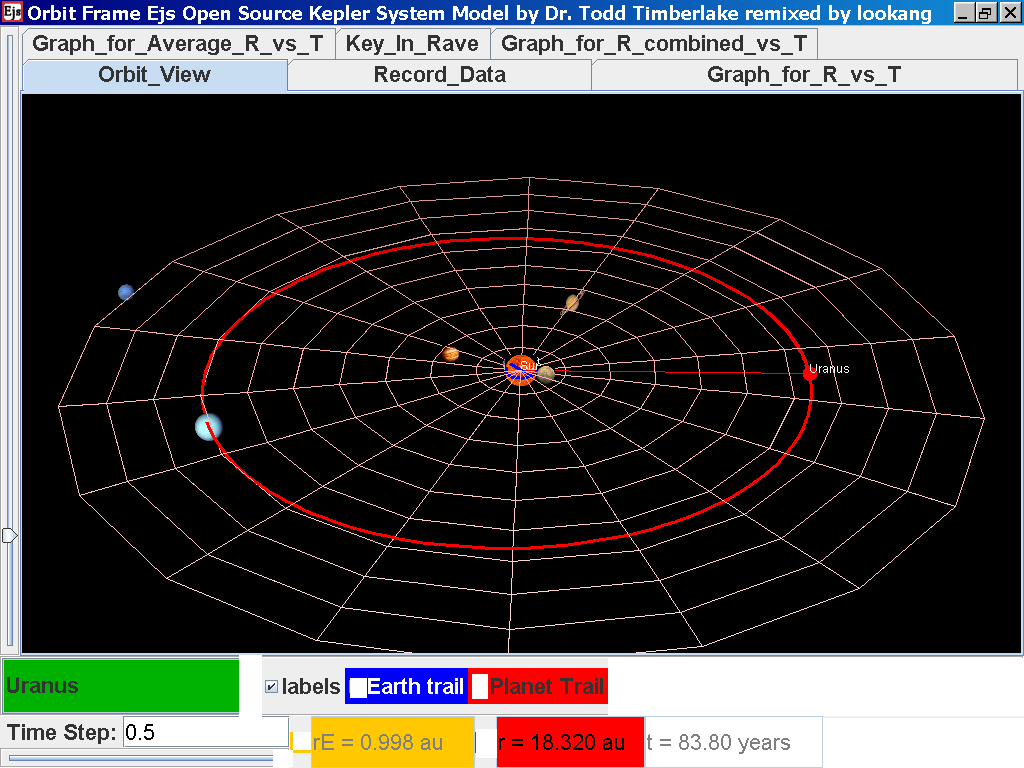
Select from the drop-down menu the planet, say Mercury to show the orbital radius and click play.

Click Pause to stop the simulation when the planet Mercury is almost at the time of 1 complete cycle or period T.

Click Step to fine tune your determination of period T, say t =0.24 years

Click on the adjacent tab Record_Data and select Record Data button to store this data on the mean radius Rm and period (time for one complete cycle) T of motion.

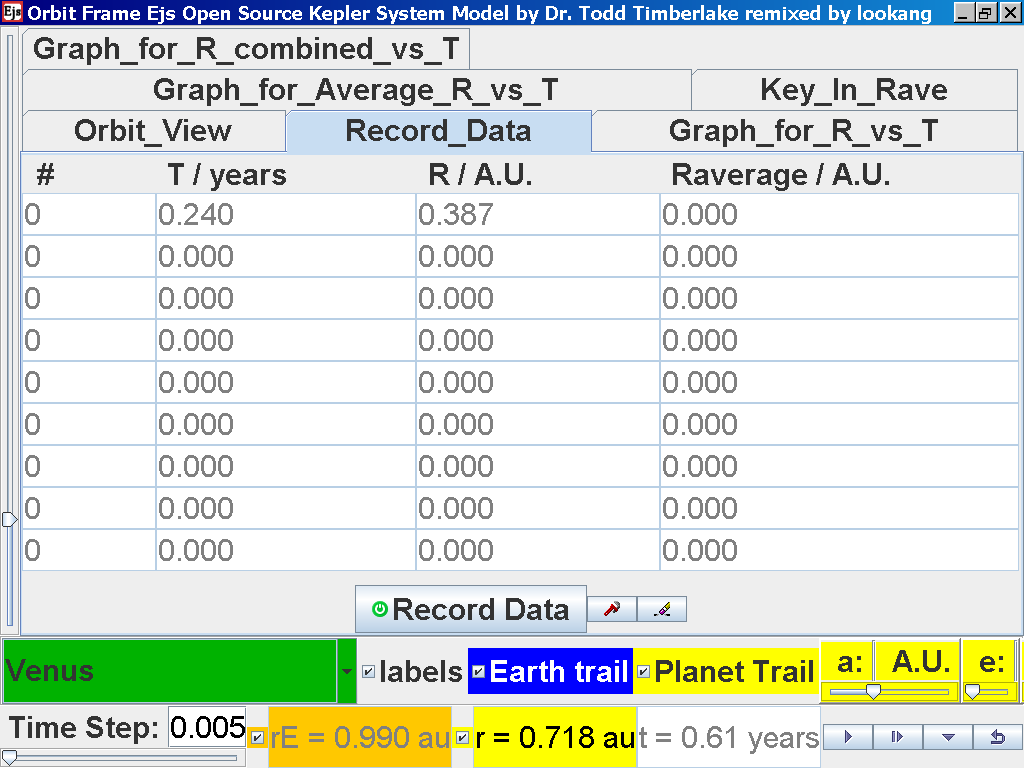
Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Venus. Play the simulation for one complete cycle.

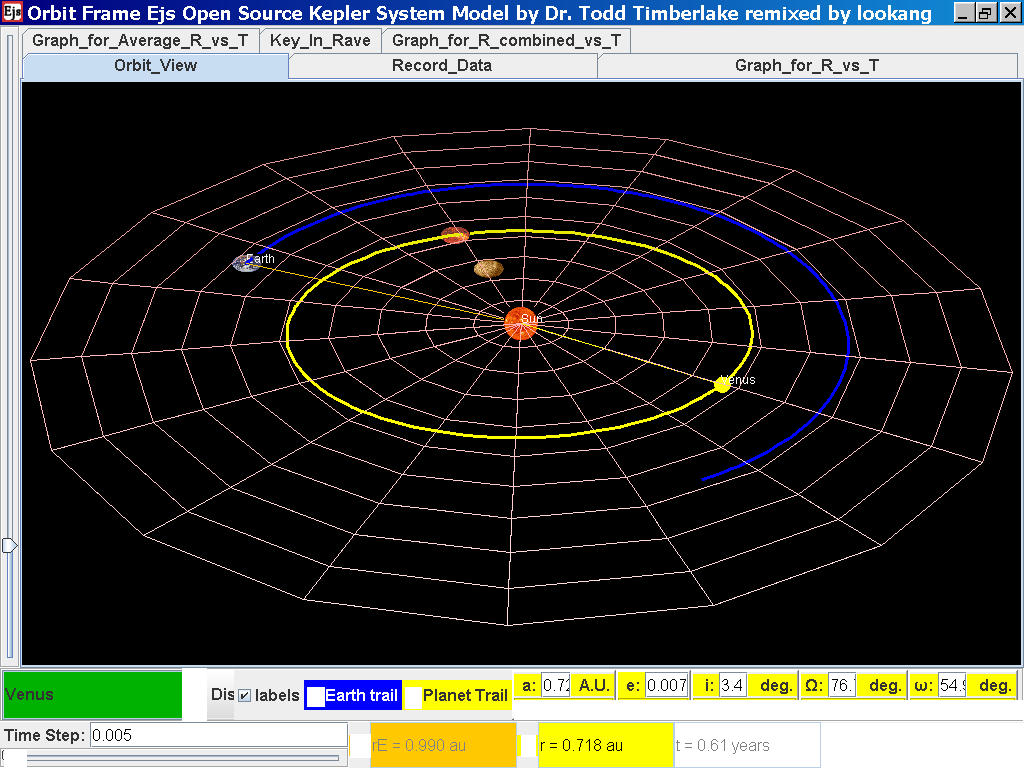
Click again on the next tab Record_Data and select Record_Data.

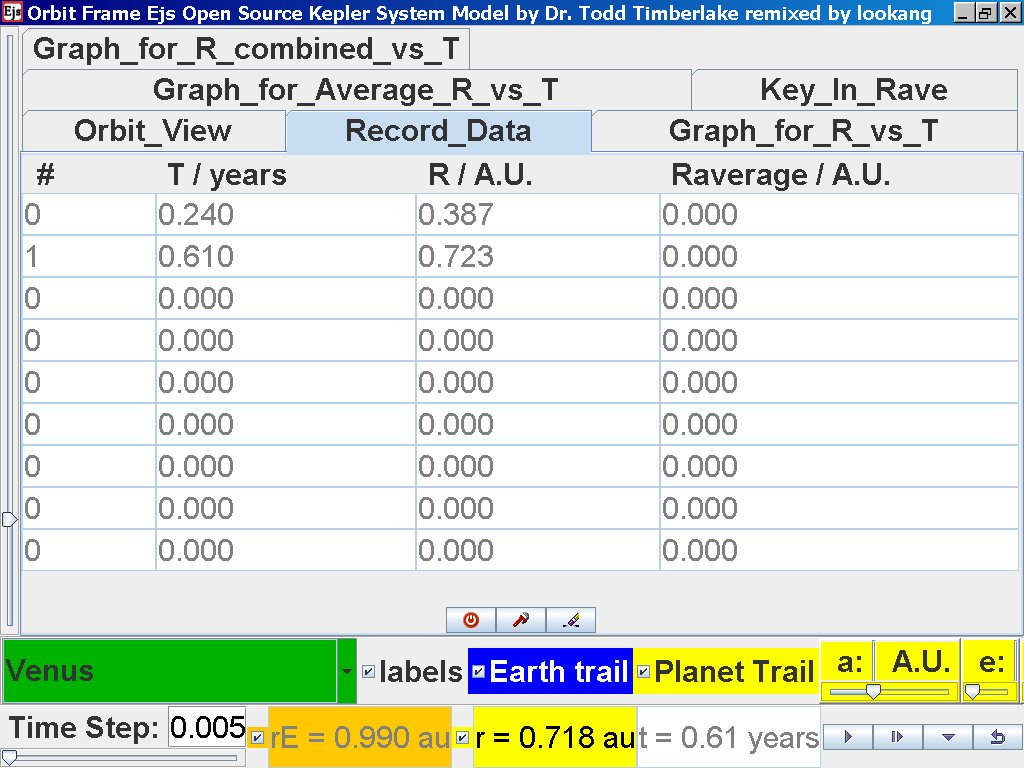
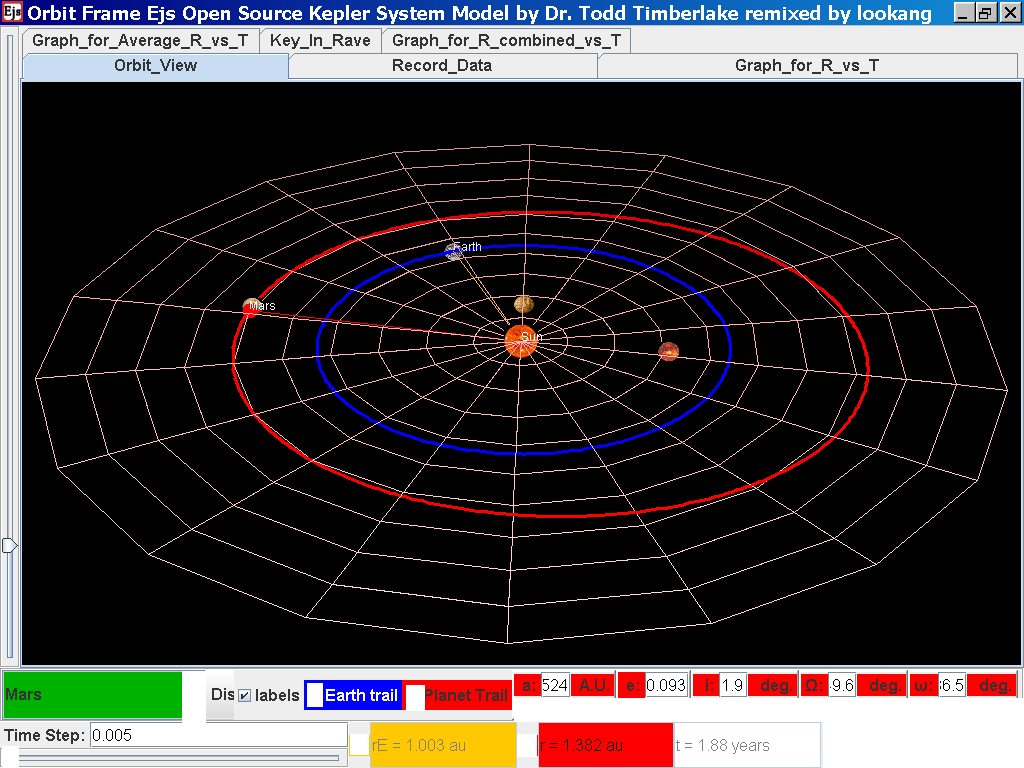
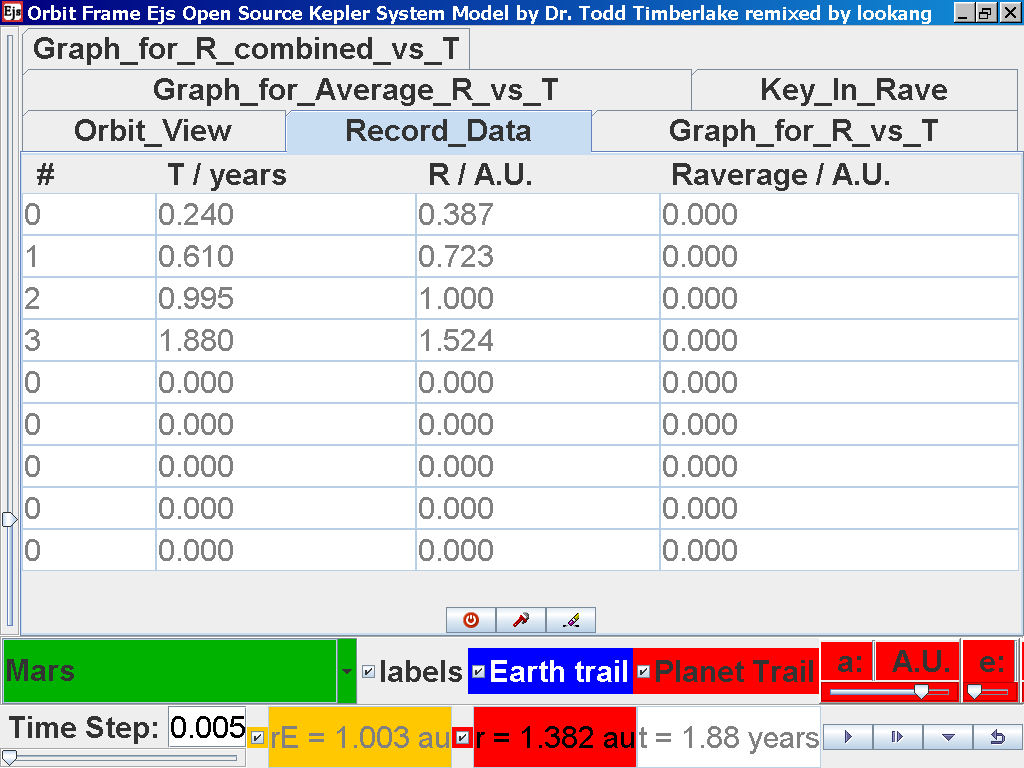
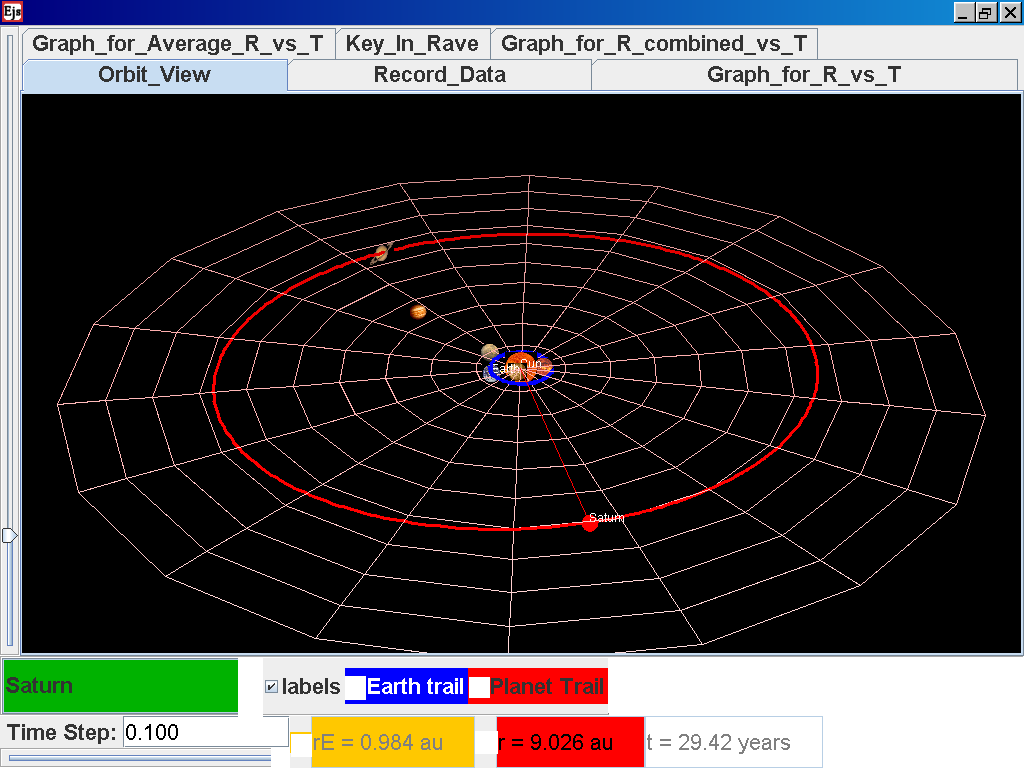
Repeat the above steps for the rest of the planets i.e. Earth, Mars, Jupiter, Saturn, Uranus, Neptune and Pluto. (Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Earth. Play the simulation for one complete cycle. )

Click again on the next tab Record_Data and select Record_Data.

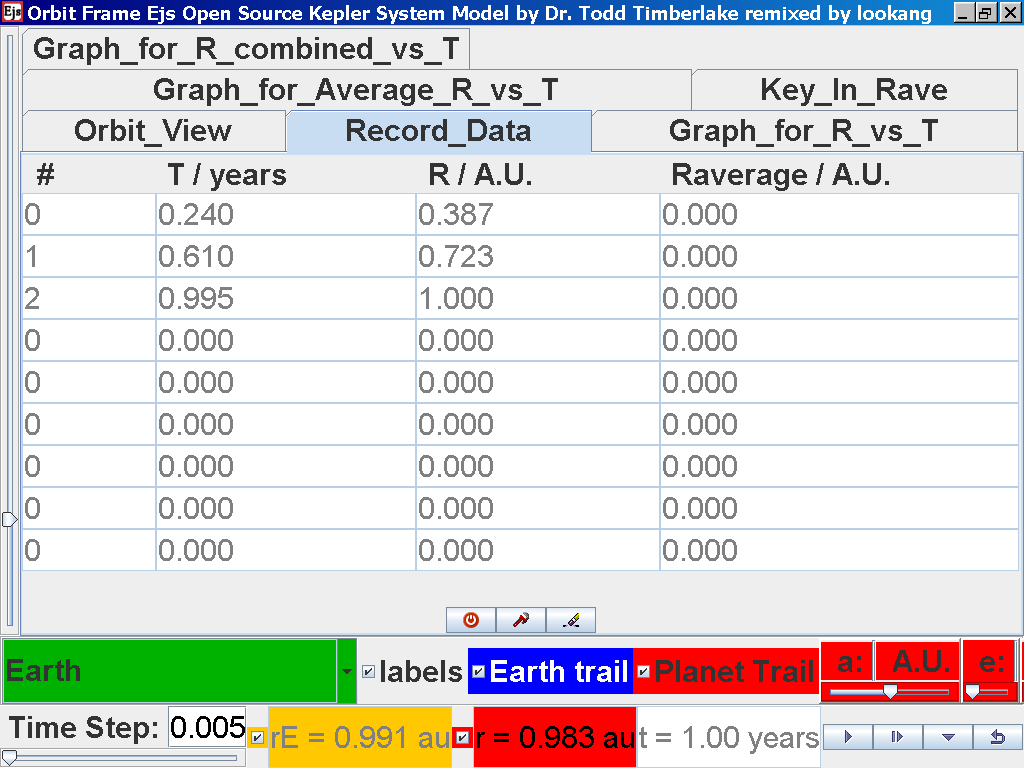
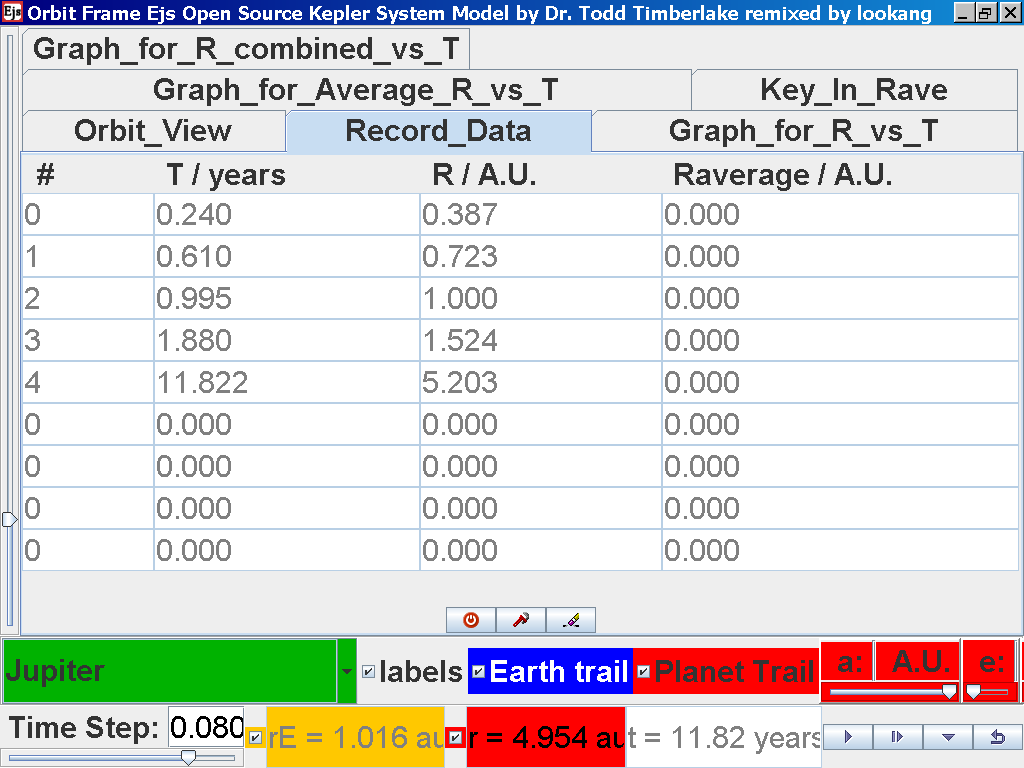
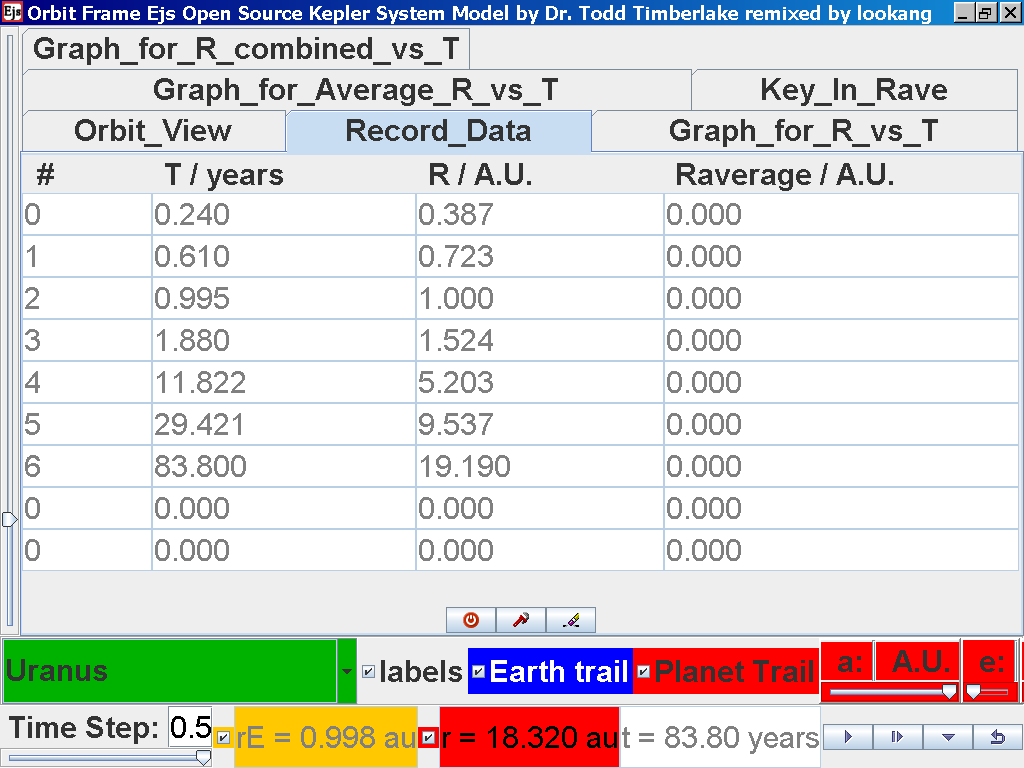
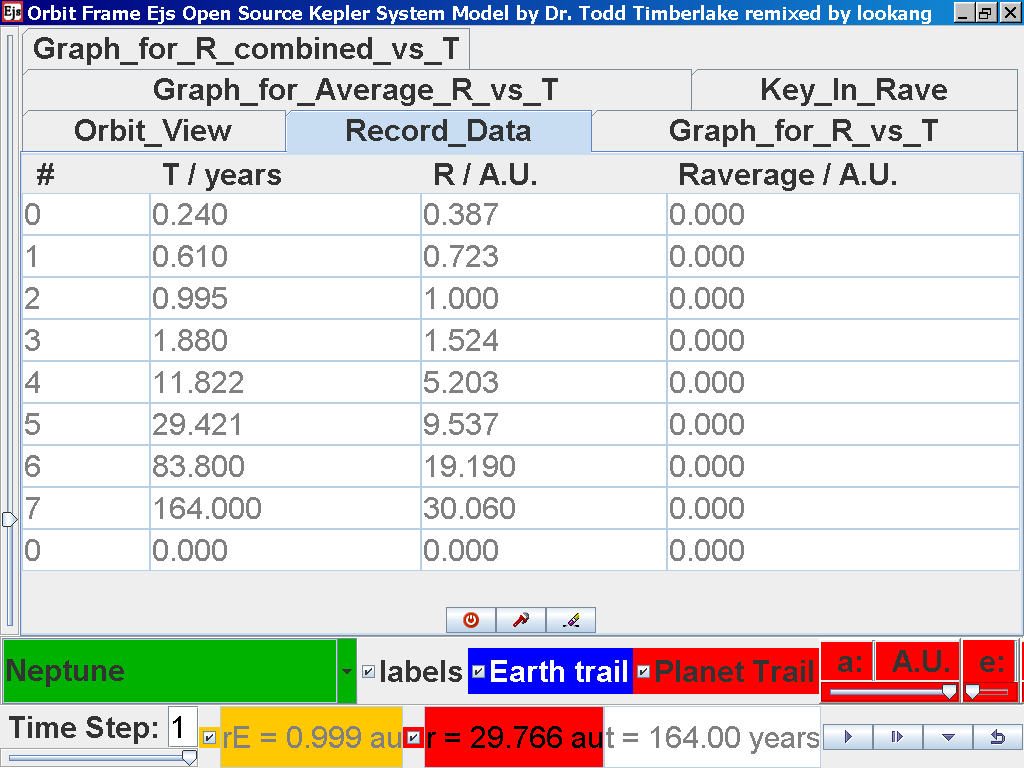
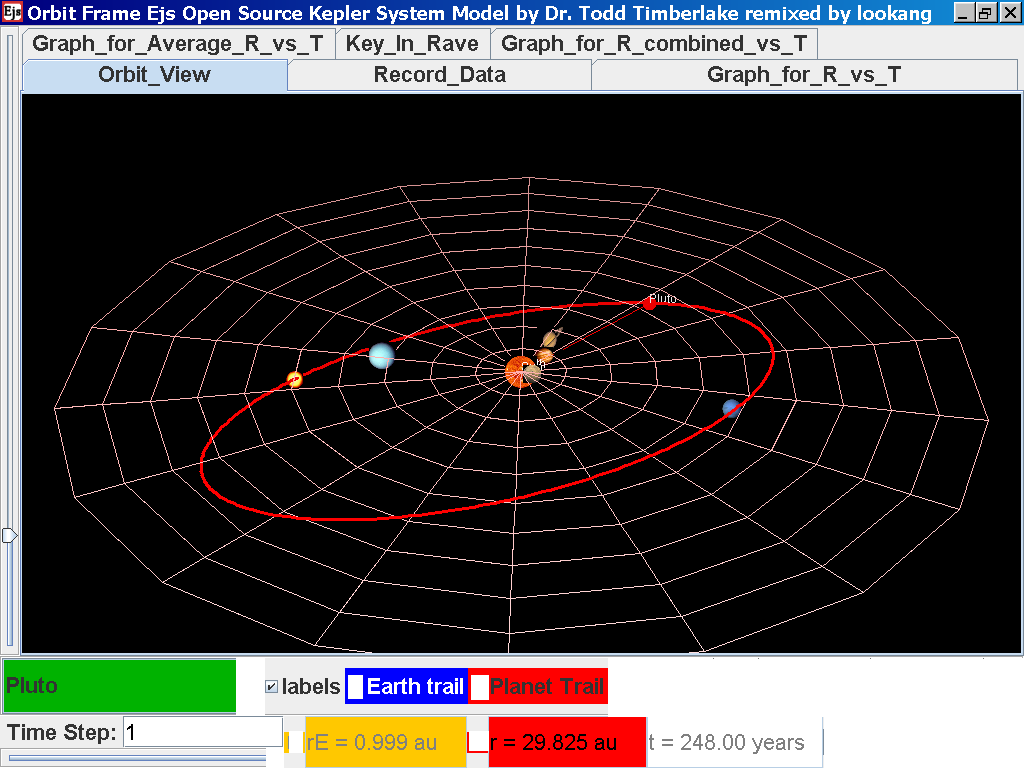
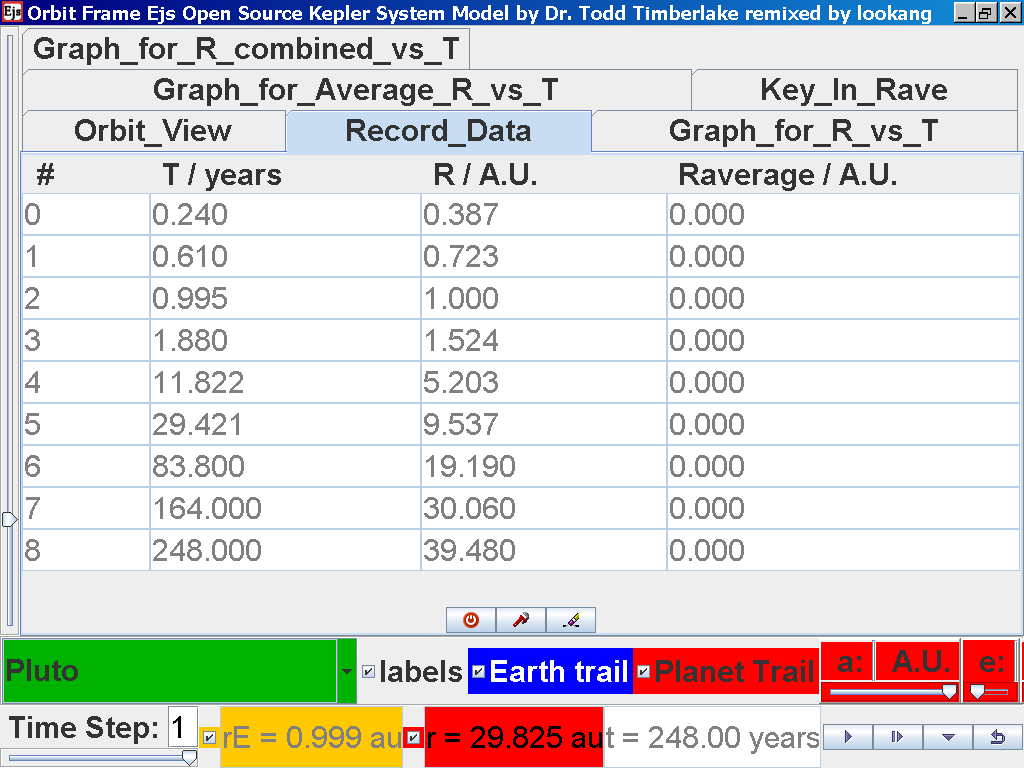
Notice all the data on the actual T /years recorded by you are slightly different compared to the mean radius of orbits R has units of A.U. (astronomical units) where by 1 A.U. = mean distance of Earth to Sun.

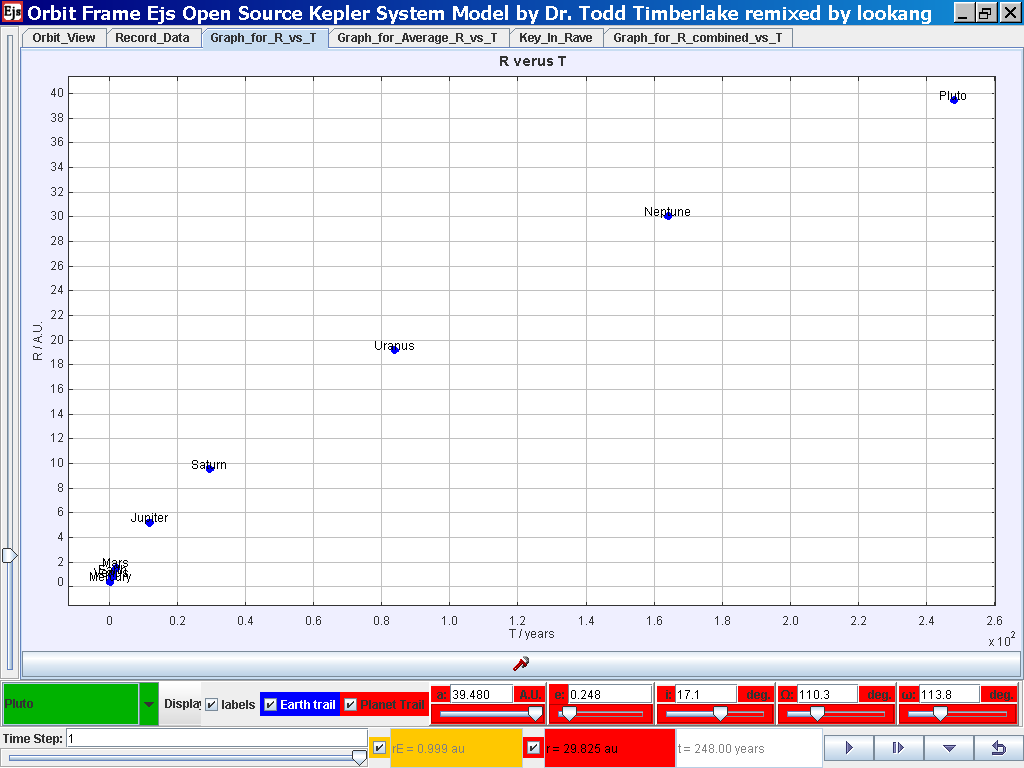
Select the tab Graph_for_R_vs_T and the simulation automatically plots the data.

Click on the Data Analysis Tool to bring up the following pop up view for further trend fitting.
Select the Data Builder Button at the top right corner

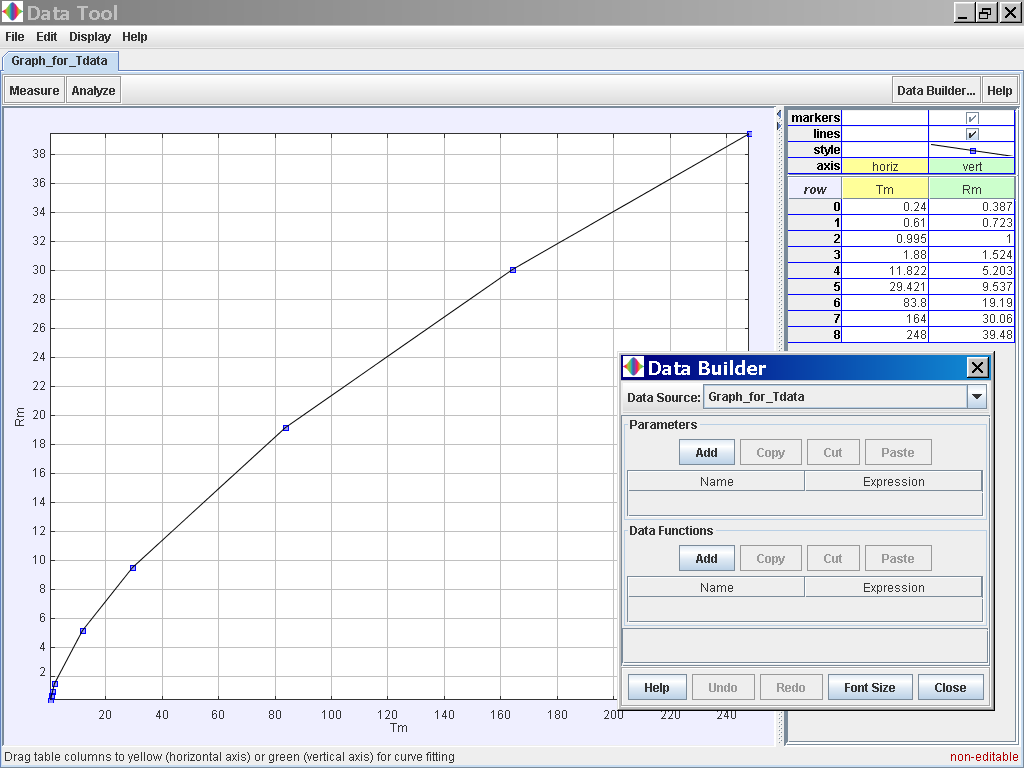
Click on the Data Function Add button to add your own functions such as T2 for T_mean² and R3 for r_mean³.

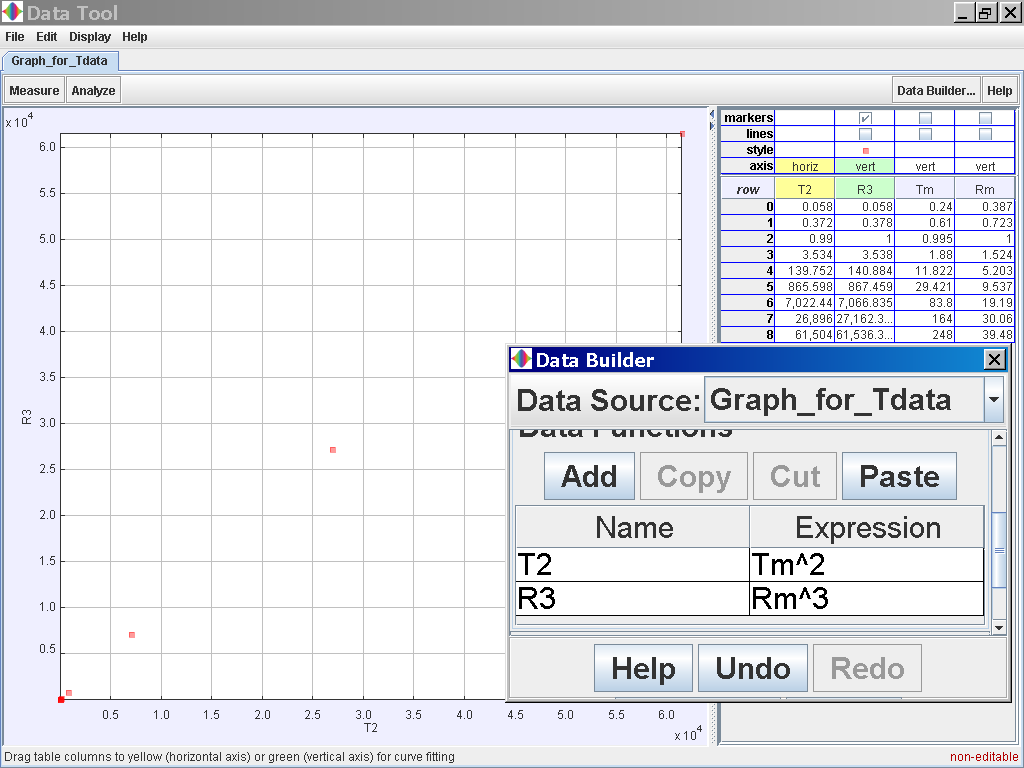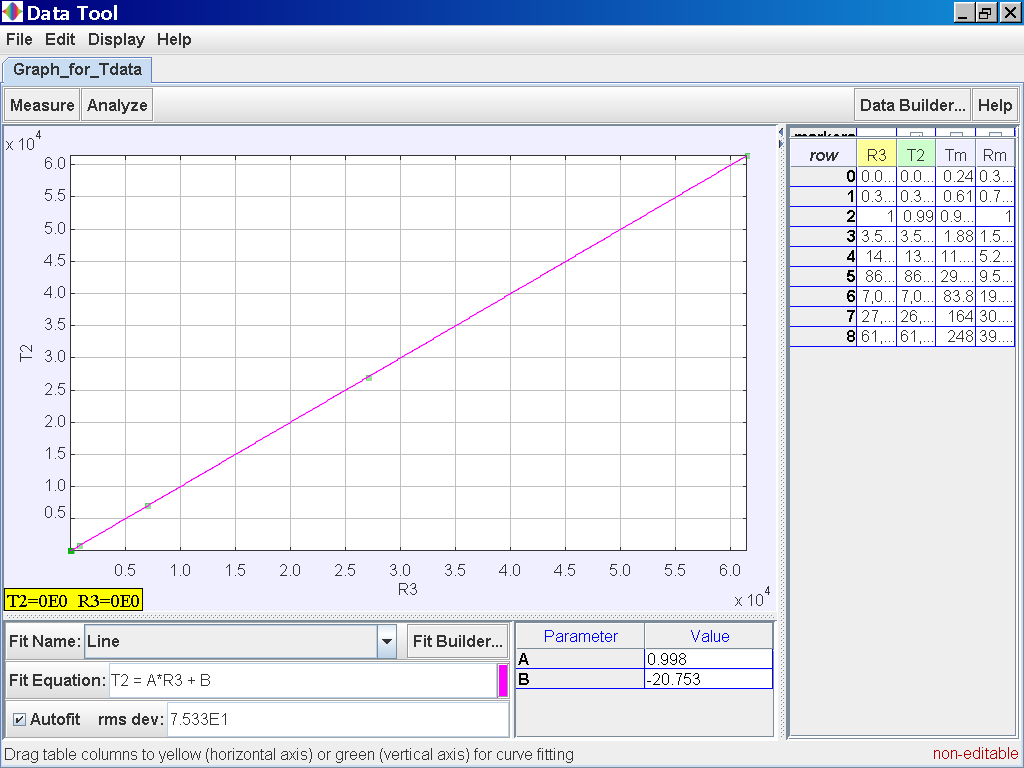
Click on the Analyse button on the top left corner and select the Linear Fit Option of which the data of T² and R³ is related by the following line fit
T² = 0.998 R³ -20.753 which suggests T² α r³

Alternatively, you can also try to plot log (T) versus log (R)

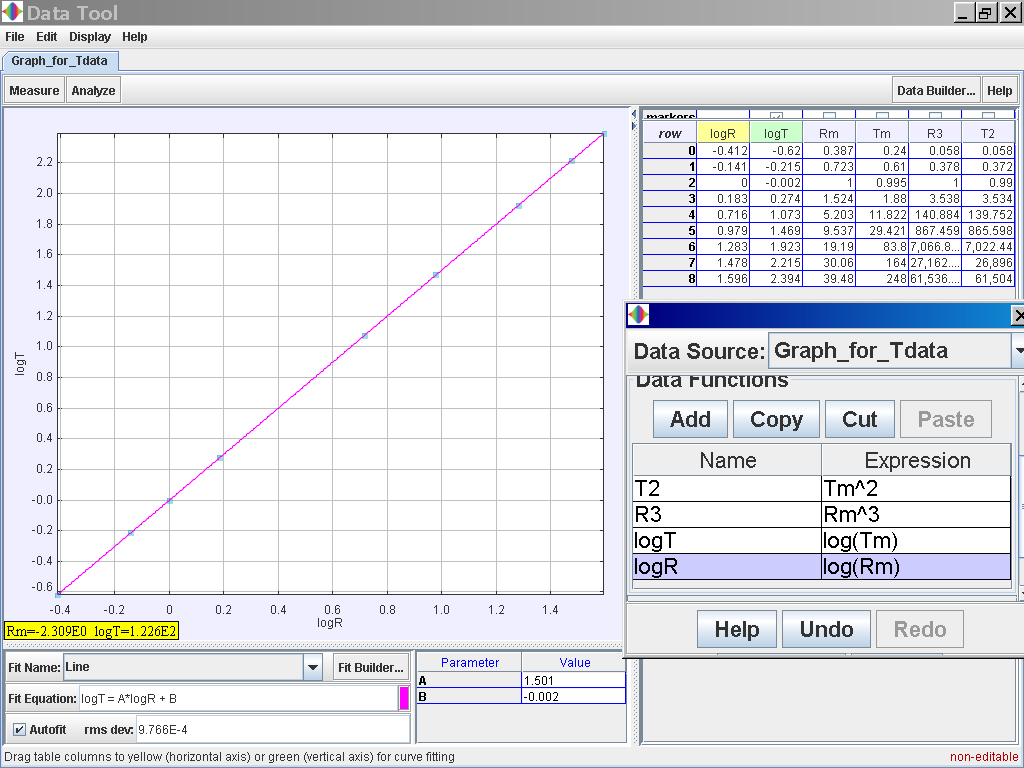
Notice that log (T) = 1.501 log (R) -0.002 which suggests the relationship of T α r^1.5 or simply T² α r³

7.5.1.4 YouTube

https://youtu.be/jt88koyZQuw Discovering Kepler 3rd System by inquiry collect data like scientists

7.5.1.5 Java simulation for the full inquiry described above

http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejs/ejs_model_KeplerSystem3rdLaw09.jar

7.5.1.6 Model, you can record down the time for each planet's one revolution to determine if T² α r³is valid

Translations

Code	Language		Translator	Run

Credits

lookang (This email address is being protected from spambots. You need JavaScript enabled to view it.); Todd TimberLake

http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejss_model_gravity09/gravity09_Simulation.xhtml

Apps

Cover art https://play.google.com/store/apps/details?id=com.ionicframework.gravity091app597842

Kepler’s Third Law

It was stated that the gravitational force acting on a satellite in orbit is the centripetal force to keep it in circular motion.

i.e.              ΣF = mrω2
            G m M r 2 = m r ω 2

recalling in circular motion,  ω = 2 πT
Hence,      G m M r 2 = m r ω 2 = m r( 2 π T ) 2

can be simplified to an equation involving T and r

T 2 = 4 π 2 G M r 3

This is the Kepler’s Third Law, which states that the square of the period of an object in circular orbit (i.e. the gravitational force acts as the centripetal force) is directly proportional to the cube of the radius of its orbit. T2 α r3

Note:
• The Kepler’s Third Law is only applicable to masses in circular orbit, whereby the gravitational force is the only force acting on it to act as its centripetal force.

Complete ICT inquiry worksheet 2 to build your conceptual understanding on the Kepler’s Third Law.

This series of screenshot serves to guide your inquiry

Select from the drop-down menu the planet, say Mercury to show the orbital radius and click play.

Click Pause the simulation when the planet Mercury is almost at the time of 1 complete cycle or period T.

Click Step to fine tune your determination of period T, say t =0.24 years

Click on the adjacent tab Record_Data and select Record Data button to store this data on the mean radius Rm and period (time for one complete cycle) T of motion.

Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Venus. Play the simulation for one complete cycle.

again click on the next tab Record_Data and select Record_Data.

Now the steps need to be repeated for the rest of the planets. Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Earth. Play the simulation for one complete cycle.

again click on the next tab Record_Data and select Record_Data.

Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Mars. Play the simulation for one complete cycle

again click on the next tab Record_Data and select Record_Data.

Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Jupiter. Play the simulation for one complete cycle and increase the time step = 0.08 years reduces the time needed to wait for one cycle.

again click on the next tab Record_Data and select Record_Data.

Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Saturn. Play the simulation for one complete cycle

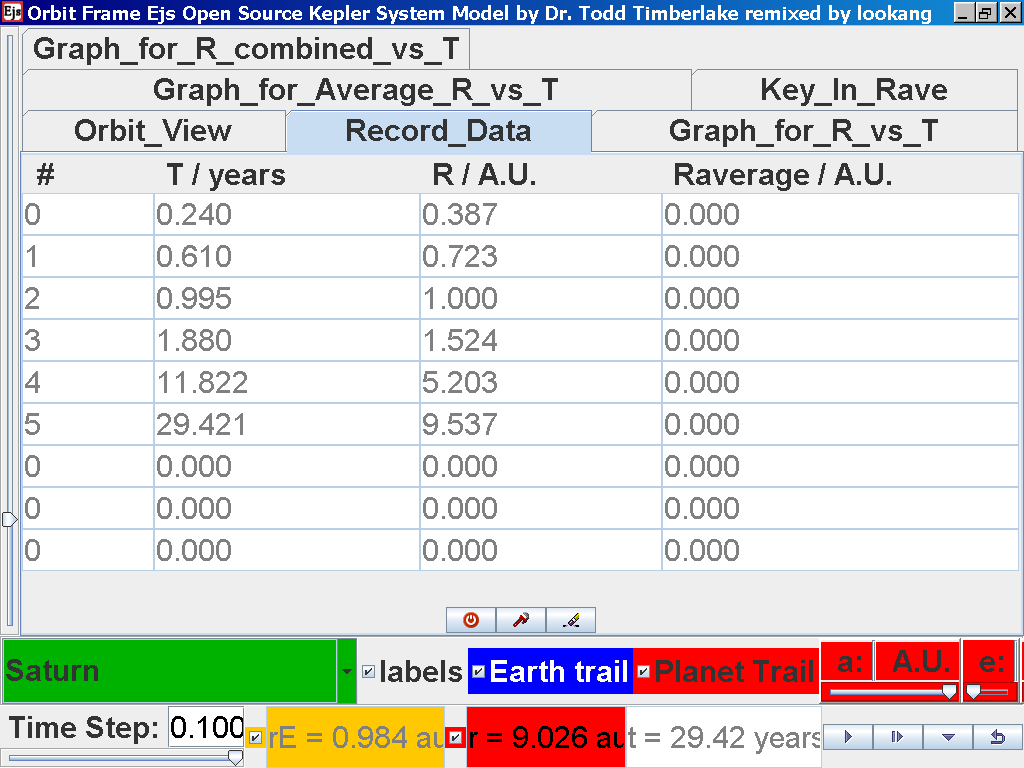
again click on the next tab Record_Data and select Record_Data.

Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Uranus. Play the simulation for one complete cycle

again click on the next tab Record_Data and select Record_Data.

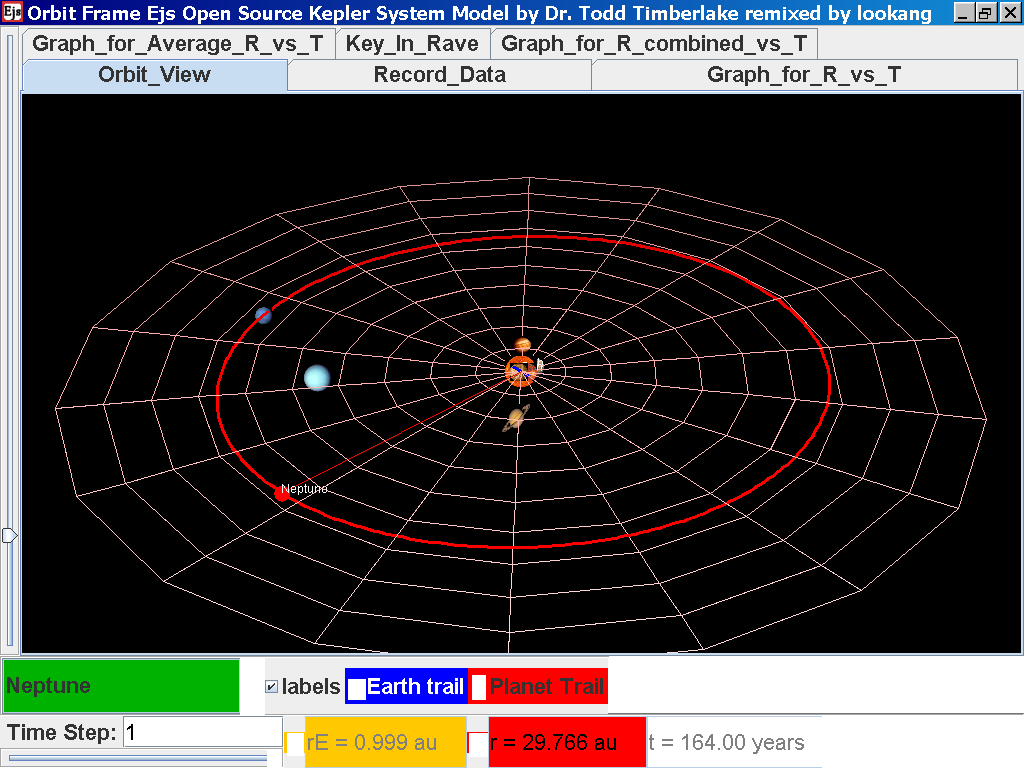
Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Neptune. Play the simulation for one complete cycle

again click on the next tab Record_Data and select Record_Data.

Click back to the Orbit_View and to go to the next planet to collect data, select from the drop down menu again and select the next planet say Pluto. Play the simulation for one complete cycle

again click on the next tab Record_Data and select Record_Data.

Notice all the data on the actual T /years recorded by you is slightly different and the mean radius of orbits R / A.U. astronomical units which 1 A.U. = mean distance of Earth to Sun.

Select the tab Graph_for_R_vs_T and the simulation automatically plots the data.

Click on the Data Analysis Tool to bring up the following pop up view for further trend fitting.
Select the Data Builder Button at the top right corner

Click on the Data Function Add button to add your own functions such as T2 for Tmean2 and r3 for rmean3.
Click on the Analyse button on the top left corner and select the Linear Fit option of which the data of T2and R3 is related by the following line fit
T2 = 0.998 R3 -20.753 which suggests T2 α r3

Alternative activity, you can also try to log (T) versus log (R)
notice again log (T) = 1.501 log (R) -0.002 which suggests the same relationship of T α r1.5 or simply T2α r3

Versions

Worksheets

end faq

{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}

5 1 1 1 1 1 1 1 1 1 1 Rating 5.00 (3 Votes)

Details: Written by Loo Kang Wee; Parent Category: 02 Newtonian Mechanics; Category: 08 Gravity; Published: 24 September 2015; Created: 24 September 2015; Last Updated: 14 August 2018; Hits: 13219

Breadcrumbs