About

For Teachers

- ping.wmv
- ping-frame2.gif
- ping-frame1.wmv
- ping-frame.wmv
- ping-frame.gif

Credits

Author: Ning video, Loo Kang model
Contact: This email address is being protected from spambots. You need JavaScript enabled to view it.

Version

http://weelookang.blogspot.sg/2016/08/ping-pong-ball-rebounce-model.html

"Tracker Ping Pong Ball Falling: JavaScript HTML5 Applet Simulation Model"

This document explores the free fall of a ping pong ball using a custom JavaScript and HTML5 applet simulation model. It delves into the effects of air resistance, mass, and initial conditions on the ball’s motion, providing insights into its descent and terminal velocity.

Study Guide:

Objective:

• Simulate and analyze the motion of a ping pong ball during free fall.
• Investigate the impact of drag force and terminal velocity.

Key Concepts:

1. Free Fall with Air Resistance:

   • Unlike ideal free fall, air resistance affects the ball’s motion significantly due to its lightweight nature.

2. Terminal Velocity:

   • The constant velocity reached when gravitational force equals drag force.

3. Drag Coefficient:

   • Determines how the shape and surface area of the ball influence its descent.

4. Simulation Modeling:

   • Using HTML5 and JavaScript to create an interactive model for visualizing motion parameters.

Experiment Overview:

• Setup:
  A virtual environment is created using JavaScript and HTML5. The simulation visualizes a ping pong ball dropped from a height under the influence of gravity and air resistance.

• Procedure:

  1. Initialize the simulation with input parameters: mass, drag coefficient, and initial height.
  2. Run the simulation and observe the ball’s motion.
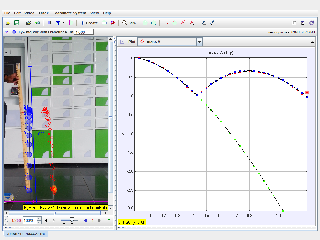
  3. Analyze graphs of velocity vs. time, displacement vs. time, and acceleration vs. time.

• Observation Points:

  • Time taken to reach terminal velocity.
  • Variations in velocity due to drag.
  • Impact of changing initial parameters like mass or drag coefficient.

Questions to Consider:

1. What role does air resistance play in the motion of the ping pong ball?

   • Answer: It opposes the ball's downward motion, reducing acceleration and leading to terminal velocity.

2. How does the drag coefficient influence terminal velocity?

   • Answer: A higher drag coefficient decreases terminal velocity due to increased resistance.

3. Why is the ping pong ball particularly affected by drag?

   • Answer: Its lightweight and relatively large surface area make drag forces more significant compared to its weight.

4. How can the simulation be customized?

   • Answer: Users can adjust parameters such as mass, height, and drag coefficient to explore different scenarios.

5. What does the velocity-time graph reveal?

   • Answer: The graph shows initial acceleration, followed by a plateau as the ball reaches terminal velocity.

Applications:

• Physics Education: Provides an interactive way to teach concepts of drag and terminal velocity.
• Simulation Design: A practical example of modeling physical systems using coding.
• Sports Science: Enhances understanding of aerodynamics in lightweight sports equipment.

FAQ:

1. Why use a simulation for this study?

   • Simulations allow controlled experimentation with adjustable parameters, making them ideal for understanding complex systems like drag forces.

2. Can the simulation handle real-world factors like wind?

   • Wind effects can be added by incorporating horizontal forces in the model.

3. What are the limitations of the model?

   • Simplifications such as neglecting rotational effects and environmental variability.

4. How does this apply to real-life scenarios?

   • Insights from the model apply to designing equipment like parachutes, lightweight projectiles, and sports gear.

5. Can I extend the simulation for other shapes or objects?

   • Yes, by modifying the drag coefficient and mass parameters, you can simulate the motion of different objects.

Ping Pong Ball Rebounce Model
Model building Process

Select Dynamic Model Cartesian, propose inital model say Fy = -mg
add parameter g = 9.81 since assume m =1 by default
determine vy when t=0, which is found via analysis to be vy = -0.6
Fy = -mg-kvy where kvy is drag force
fine tune value of k until match data k is found to be k = 1.11
this completes the fall under drag model 
to add the rebounce force
propose computational thinking, if (t< thitground , true, false )
nestted if statements to achieve answer
can you get the same model?, need to assume contact time of 0.02
the model suggests contact force is 390 N for a mass of ping pong m=1kg 
if ping pong mass is measured, just key in to find the contact force.
enjoy!

 end faq

{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}