Translations

Code	Language		Translator	Run

Credits

Author name; Fu Kwun Hwang; loo kang WEE

http://iwant2study.org/lookangejss/02_newtonianmechanics_3dynamics/ejss_model_bulletBoxwee/bulletBoxwee_Simulation.xhtml

Briefing Document: Bullet and Box HTML5 JavaScript Simulation Model

1. Overview

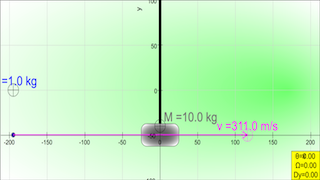
This document reviews the "Bullet and Box HTML5 JavaScript Simulation Model," an interactive physics simulation developed as part of the Open Educational Resources / Open Source Physics @ Singapore initiative. This model, built using HTML5 and JavaScript, is designed to demonstrate the principles of energy and momentum conservation in a collision scenario. It allows users to explore how a bullet's velocity impacts the resulting pendulum motion of a block it becomes embedded in. The simulation also explores what happens when the bullet passes through the block. The model is accessible through a web browser on various devices, including desktops, laptops, and mobile devices.

2. Core Concepts

• Collision and Momentum: The simulation visualizes the principle of momentum conservation. When the bullet (mass m, velocity v) embeds into the block (mass M), the combined mass (m+M) moves as a pendulum. The initial momentum of the bullet is transferred to the bullet-block system.
• Kinetic and Potential Energy Conversion: The kinetic energy of the bullet is converted to the kinetic energy of the bullet-block system, which is then converted to gravitational potential energy as the pendulum rises. The maximum height of the pendulum is directly linked to the initial kinetic energy. The simulation states, "the conversion of KE energy predicts a higher height due to PE completely conversion from initial KE."
• Fixed Force Assumption: The simulation simplifies the interaction between the bullet and the box by assuming a fixed force (F0=1350). This assumption is acknowledged as crucial for determining whether the bullet remains embedded in the block or passes through it, and not a variable dependent on the velocity of the bullet.. As the source explains, "the force between bullet and the box is assumed to be a fixed value in this simulation. Is this a good assumption? My answer: Yes, it is essential for the determination of the whether the bullet is stuck on the block or pass through the block, i hardcoded it inside as F0=1350 permanently instead of a variable of F0= bvxvx".
• Simulation Variables: Users can manipulate the initial speed of the bullet and observe the resulting changes in the maximum height reached by the pendulum.
• Comparison: The model also provides an opportunity to compare the scenario of the bullet sticking in the block with the scenario where it passes through, and to observe that the resulting height of the block in the pass-through scenario is relatively constant.

3. Key Features & Functionality

• Interactive Simulation: The simulation is embedded in an iframe, allowing for seamless integration into web pages.
• Adjustable Parameters: The initial speed of the bullet is the primary variable users can change.
• Visual Feedback: The simulation shows the motion of the bullet and the block, allowing users to visually track changes in kinetic and potential energy and to measure the maximum height of the pendulum.

4. Pedagogical Uses

• Conceptual Understanding: The model allows students to explore and understand the relationship between bullet speed, and the resulting height of the pendulum, allowing students to make the link between KE and PE.
• Inquiry-Based Learning: By manipulating the initial speed, students can test hypotheses and make predictions.
• Visual Representation: The visual nature of the simulation helps students grasp abstract concepts of energy and momentum transfer.
• Measurement: The simulation can be used to quantitatively explore the physical phenomena at play.

5. Technical Details

• Technology: The simulation is built using HTML5 and JavaScript, making it compatible with most modern browsers and devices, including Android/iOS devices and ChromeBooks.
• Credits: The model is attributed to Fu Kwun Hwang and Loo Kang Wee. The original work was created by Professor Fu-Kwun Hwang and can be found at http://enjoy.phy.ntnu.edu.tw/ntnujava/index.php?topic=448.0. The HTML5 conversion was developed by Loo Kang Wee, as can be found here: http://weelookang.blogspot.sg/2017/05/bullet-and-box-html5-javascript.html

6. Context & Wider Project

• Open Educational Resources: The simulation is part of a broader collection of open educational resources developed in Singapore.
• Open Source Physics: The model exemplifies the principles of Open Source Physics, emphasizing free access to resources for education.
• EasyJavaScriptSimulation (EJS): The simulation is created using EJS, a tool for creating interactive simulations.
• Diverse Resources: The accompanying text provides access to a wide array of other physics simulations and educational resources developed by the same initiative, showcasing the scope of their project. These simulations cover diverse topics ranging from mechanics and waves to electromagnetism, nuclear physics and even games to help with recycling, demonstrating the breadth of their efforts to improve science education in Singapore.

7. Quotes from Source:

• "A bullet of mass m and speed v embeds in a block of mass M suspended by a string. The block and bullet, of total mass m+M, then moves as a pendulum and the maximum height it reaches can easily be measured. This apparatus ca be used to measure the speed of the bullet."
• "In this HTML5 applet, you can change the initial speed and find of the maximum height it reaches. Does it get higher with greater bullet speed? Answer: Yes, the conversion of KE energy predicts a higher height due to PE completely conversion from initial KE."
• "The force between bullet and the box is assumed to be a fixed value in this simulation. Is this a good assumption? My answer: Yes, it is essential for the determination of the whether the bullet is stuck on the block or pass through the block, i hardcoded it inside as F0=1350 permanently instead of a variable of F0= bvxvx"

8. Conclusion

The "Bullet and Box HTML5 JavaScript Simulation Model" is a valuable educational tool for exploring the principles of energy and momentum in a practical, interactive way. Its accessibility and flexibility make it a useful resource for both teachers and students interested in physics education. The wider context of Open Educational Resources / Open Source Physics @ Singapore showcases a broader commitment to creating high-quality, freely available science resources for the community.

Bullet and Box Simulation Study Guide

Quiz

Instructions: Answer the following questions in 2-3 sentences each.

1. What is the purpose of the Bullet and Box simulation?
2. How does changing the initial speed of the bullet affect the maximum height reached by the block?
3. What happens if the bullet passes through the box instead of embedding in it?
4. What assumption is made about the force between the bullet and the box in this simulation?
5. Why is the assumption of a fixed force between the bullet and the box essential for the simulation?
6. Name one other simulation resource that is mentioned in the text.
7. Who are the primary authors of this simulation?
8. What type of energy transformation is primarily demonstrated in this simulation?
9. What is the format of the simulation and how does that make it accessible to different users?
10. Where can one find the original simulation of the Bullet and Box?

Quiz Answer Key

1. The purpose of the Bullet and Box simulation is to demonstrate the principles of momentum and energy conservation, specifically how the kinetic energy of a bullet is transferred to the pendulum system when the bullet is embedded in a suspended block. It can also illustrate the relationship between initial bullet speed and the height the block reaches after impact.
2. Increasing the initial speed of the bullet will cause the block to reach a higher maximum height. This is due to the increase in initial kinetic energy transferred to the block and pendulum system, which is then converted to potential energy as the block swings upward.
3. If the bullet passes through the box, the block will still swing upwards, but the height reached will be a fixed height, approximately the same no matter the speed of the bullet because the kinetic energy and momentum transfer is reduced.
4. The force between the bullet and the box is assumed to be a fixed value, F0=1350, for the purpose of the simulation. This simplifying assumption is done to determine whether the bullet is stuck in or passes through the block.
5. This fixed force assumption is essential to allow the simulation to determine whether the bullet embeds itself in the block or passes through the block. If the force isn't constant the simulation becomes a great deal more complex.
6. One other simulation resource mentioned in the text is the "Bar Magnet Field Line Simulator JavaScript Simulation Applet HTML5".
7. The primary authors of this simulation are Fu Kwun Hwang and Loo Kang Wee.
8. The simulation primarily demonstrates the transformation of kinetic energy into potential energy, while also touching on the principles of momentum transfer.
9. The simulation is in HTML5 format, which makes it accessible across various platforms including Android/iOS devices, and Chromebook laptops.
10. The original simulation can be found at http://enjoy.phy.ntnu.edu.tw/ntnujava/index.php?topic=448.0, credited to Professor Fu-Kwun Hwang.

Essay Questions

Instructions: Answer the following questions in well-organized essays.

1. Discuss the pedagogical benefits of using simulations like the Bullet and Box model in physics education. Consider how this simulation supports student understanding of energy and momentum concepts.
2. Analyze the role of simplifying assumptions in physics simulations. How does the fixed force assumption in the Bullet and Box model contribute to its educational value, and what are its limitations?
3. Compare and contrast the scenario where the bullet embeds in the box versus the scenario where it passes through. What differences in energy transfer and momentum are highlighted in these scenarios?
4. Evaluate the accessibility and usability of the Bullet and Box simulation. How does the HTML5 format contribute to its accessibility, and what types of users would benefit most from this resource?
5. How does this simulation fit within the larger context of Open Educational Resources (OER) and Open Source Physics (OSP) initiatives? Discuss how the OER nature of the simulation impacts its utility and adoption.

Glossary of Key Terms

Kinetic Energy (KE): The energy an object possesses due to its motion. It is calculated using the formula KE = 1/2 * mv², where m is mass and v is velocity.

Potential Energy (PE): The energy an object has due to its position or condition. In this simulation, the potential energy is gravitational, based on the height of the block.

Momentum: A measure of an object's mass in motion. It is calculated as the product of an object's mass and its velocity (p=mv)

Conservation of Energy: A fundamental principle that states that energy cannot be created or destroyed, only transferred from one form to another.

Conservation of Momentum: A principle that states that the total momentum of a closed system remains constant if no external forces act upon it.

HTML5: The fifth and latest version of the Hypertext Markup Language, used to create and structure content on the web. It allows for multimedia and interactivity without requiring plugins.

JavaScript: A programming language primarily used to create interactive effects within web browsers.

Open Educational Resources (OER): Teaching and learning materials that are freely available online for anyone to use, adapt, and share, typically under an open license.

Open Source Physics (OSP): A collaborative project that develops educational software in the domain of physics, and makes it available as OER.

App

{/source}

Description

Video

[text]

 Version:

1. http://enjoy.phy.ntnu.edu.tw/ntnujava/index.php?topic=448.0 Original by Professor Fu-Kwun Hwang
2. http://weelookang.blogspot.sg/2017/05/bullet-and-box-html5-javascript.html     

Other Resources

Frequently Asked Questions: Bullet and Box Simulation

1. What is the purpose of the Bullet and Box simulation? The simulation models a scenario where a bullet embeds itself into a suspended block, causing the combined mass to swing like a pendulum. This setup is designed to explore concepts of momentum and energy conservation, specifically how the initial speed of the bullet affects the maximum height reached by the combined system. It's also used to investigate the differences between scenarios where the bullet is embedded versus passing through the block.
2. How can the Bullet and Box simulation be used in education? This simulation is a tool for physics education, primarily focusing on Newtonian mechanics, oscillations, and the principles of energy transfer and conversion. It allows students to visualize the relationship between the bullet's initial kinetic energy and the potential energy of the pendulum at its maximum height, helping them understand how these energies are converted. It can be used in classrooms using projectors or for individual study on a variety of devices, including phones and laptops.
3. What physical principles are demonstrated in the simulation? The primary principles demonstrated are the conservation of momentum and the conservation of energy. The initial momentum of the bullet is transferred to the bullet and box system. The initial kinetic energy of the bullet converts to kinetic energy of the combined mass which in turn converts to gravitational potential energy at the maximum height of the swing. The simulation allows exploration of how these energies and momentum are transformed and conserved, especially for cases where the bullet embeds in the box.
4. How does the simulation model the interaction between the bullet and the box? In the simulation, the force between the bullet and the box is simplified by using a fixed value (1350 in the code). This assumption helps to determine if the bullet becomes lodged in the box or passes through it. While not perfectly realistic, this fixed force approach simplifies the calculations while still allowing for the observation of the key concepts being explored, and allows a student to observe the difference between a bullet being embedded and passing through.
5. What happens when the bullet's speed is increased? When the bullet's initial speed is increased, the simulation demonstrates that the combined block and bullet will swing to a higher maximum height. This increased height corresponds to a higher potential energy which results from the increased initial kinetic energy of the faster bullet and supports the concept that energy is conserved and converted.
6. What does the simulation show if the bullet passes through the box? If the bullet is allowed to pass through the box in the simulation, the maximum height reached by the block tends to remain relatively consistent, regardless of the bullet's initial speed, showing that some of the initial kinetic energy of the bullet is not transferred to the block. The simulation helps illustrate that an embedding interaction allows for the full transfer of the kinetic energy in the system, versus a pass through where some of the kinetic energy is not transferred.
7. Is the simulation designed for a particular platform? The simulation is designed to be platform independent as it was developed using HTML5 and Javascript, making it accessible on various devices including desktops, laptops, tablets, and smartphones. It's also compatible with common browsers, including those on Chromebooks, without needing to install any additional software.
8. What are the limitations of the Bullet and Box simulation? The simulation simplifies the real-world physics of the bullet-box interaction. Specifically, it assumes a fixed force between the bullet and the box, instead of using a more complex model such as a variable force that could depend on speed. This simplification is a deliberate choice to keep the simulation accessible and computationally efficient for educational purposes, focusing on the primary energy and momentum transfer concepts rather than highly accurate modeling of the material interaction.