
About
This email address is being protected from spambots. You need JavaScript enabled to view it.
For Teachers
Credits
Author: Eka Cahya Prima
Contact: This email address is being protected from spambots. You need JavaScript enabled to view it.
Rolling Cylinders 501 (Master-Level Dynamics) by Eka Cahya Prima"
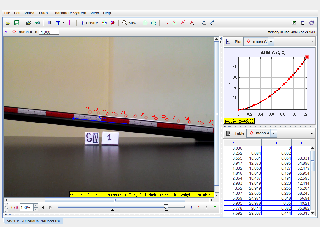
This advanced study investigates the intricate physics of rolling cylinders, focusing on high-precision modeling, chaotic interactions, and the application of non-linear dynamics principles. The experiments explore systems with irregular shapes, non-uniform mass distributions, and variable environmental conditions. Tracker software is used extensively for data collection, analysis, and dynamic simulation.
Study Guide:
Objective:
- Understand the effects of irregularities and environmental variability on rolling dynamics.
- Explore chaotic systems and their implications for real-world applications.
Key Concepts:
-
Non-Linear Dynamics:
- Understanding non-linear relationships between force, motion, and geometry in rolling systems.
-
Irregular Shapes and Mass Distributions:
- How non-uniform shapes and masses alter rolling stability and trajectories.
-
Chaotic Interactions:
- Studying systems that exhibit sensitivity to initial conditions and unpredictable long-term behavior.
-
Dynamic Simulations:
- Using Tracker software to simulate and predict motion in advanced rolling systems.
Experiment Overview:
-
Setup:
Rolling experiments include cylinders with varied shapes, mass distributions, and material properties, conducted on complex surfaces with variable inclines. Tracker software and high-precision sensors capture motion details. -
Procedure:
- Roll irregularly shaped cylinders on complex surfaces.
- Introduce disturbances to observe sensitivity and chaos.
- Analyze motion data to identify patterns and anomalies.
- Simulate advanced systems using Tracker for predictive modeling.
-
Observation Points:
- Irregular path dynamics.
- Stability under varying conditions.
- Identification of chaotic behaviors.
Questions to Consider:
-
How do irregular shapes affect rolling dynamics?
- Answer: Irregular shapes create uneven moments of inertia and varying frictional forces, leading to unique rolling behaviors.
-
What is the role of chaos in rolling systems?
- Answer: Chaotic systems demonstrate high sensitivity to initial conditions, causing small variations to significantly alter motion over time.
-
How does mass distribution influence stability?
- Answer: Uneven mass distribution shifts the center of mass, affecting balance and trajectory.
-
Can rolling patterns be predicted in non-linear systems?
- Answer: While precise predictions are challenging, simulations can provide probabilistic insights and trend analysis.
-
How does Tracker software enhance understanding of chaos?
- Answer: Tracker captures detailed motion data that allows for in-depth analysis of seemingly random behaviors.
Applications:
- Physics Research: Insights into non-linear dynamics and chaotic systems.
- Engineering: Design of rolling components for irregular terrains and non-standard applications.
- Material Science: Studying effects of irregularities in manufactured components.
FAQ:
-
Why study irregular and chaotic rolling systems?
- Real-world systems often feature irregularities and unpredictability, making these studies highly applicable.
-
What challenges are associated with these experiments?
- Controlling and measuring small irregularities and predicting chaos require advanced equipment and analytical tools.
-
Can Tracker predict chaotic behaviors?
- Tracker provides data for modeling and trend analysis, which helps in understanding chaotic dynamics indirectly.
-
What are practical benefits of these studies?
- Improved designs for rolling systems in uneven environments and a better understanding of material behaviors.
-
How can this study be expanded further?
- Incorporate AI-based simulations for more robust predictions and explore multi-body chaotic systems for broader insights.
Research
http://scitation.aip.org/
- Details
- Parent Category: 03 Motion & Forces
- Category: 02 Dynamics
- Hits: 5831
