Translations

Code	Language		Translator	Run

Credits

Francisco Esquembre; Flix J. Garca Clemente

http://iwant2study.org/lookangejss/01_measurement/ejss_model_DataFittingwee/DataFittingwee_Simulation.xhtml

Briefing Document: Data Fitting JavaScript HTML5 Applet Simulation Model

1. Overview

This document reviews the "Data Fitting JavaScript HTML5 Applet Simulation Model" developed by Francisco Esquembre and Félix J. García Clemente, available through Open Educational Resources / Open Source Physics @ Singapore. This model is a JavaScript-based interactive tool designed to help users understand the process of fitting a polynomial curve to a set of data points. It utilizes the Numeric JS library for solving linear equations related to the least squares approximation.

2. Main Themes and Ideas

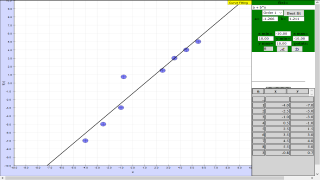
• Interactive Data Fitting: The core functionality of the applet revolves around allowing users to interactively add data points to a graph by clicking on the plotting panel. Users can then manipulate parameters of a polynomial function to visually approximate the best fit for the given data set.
• Polynomial Curve Fitting: The model emphasizes fitting data using polynomial functions of the form y = f(x), where 'f(x)' can be adjusted using parameters a, b, c, d, and e. This allows students to explore the relationship between polynomial coefficients and the resulting curve's shape.
• Least Squares Approximation: A key element of the simulation is its use of the Numeric JS library to calculate the best-fit polynomial based on the least squares method. This provides an analytical foundation for the visual fitting process. The simulation exposes the user to the idea that "this model demonstrates how to use the Numeric JS model element to solve the system of linear equations required for the least squares approximation."
• Educational Focus: The applet is explicitly designed for educational purposes, targeting secondary and junior college students. The "Sample Learning Goals Procedure" prompts users to "Add data to the panel and then adjust the parameters of the polynomial y = f(x), in order to obtain a good fit using the a , b , c , d , and e parameters."
• Open Educational Resource: The applet is distributed under an open license, promoting access and adaptation of this educational resource. This aligns with the goals of "Open Educational Resources / Open Source Physics @ Singapore"

3. Key Features and Functionality

• Interactive Point Input: Users can add data points by clicking within the plotting panel. There's a limit to the number of points to be added.
• Parameter Adjustment: Users can adjust parameters a, b, c, d, and e to manipulate the shape of the polynomial function y = f(x).
• "Best Fit" Button: This button calculates and displays the polynomial that best fits the data using the least-squares method, allowing users to compare their manual fitting to the computer’s calculation. "Use the best fit button to compare your fit to the the best possible polynomial fit". The "computeBestFit()" method can be customized to change the fitting algorithm.
• Customization: The "computeBestFit()" method within the Custom panel of the model can be edited to modify the best-fit algorithm, thus providing an avenue for deeper learning and exploration.
• Mobile and Desktop Compatibility: Designed as a JavaScript HTML5 applet, the model is compatible across multiple platforms including Android/iOS, Windows/MacOSX/Linux, and ChromeBook Laptops.

4. Mathematical and Technical Details

• Least Squares Method: The applet applies the least squares method to find the best fitting curve. As stated in the description, "The objective is to minimize the sum: ... To this end, we have to differentiate with respect to ci, and equate to zero: Obtaining the follow system: where (a,b)dare defined as:". This explains the underlying mathematical principles at the heart of the fitting process.
• Basis Functions: The documentation also notes that the function being fit is a linear combination of a basis of linear independent functions: "{1,x,x2,x3,...,xm}". This highlights the role of basis functions in representing polynomials.
• Numeric JS Library: The model utilizes Numeric JS to handle the mathematical computations required for solving the system of linear equations used in the least squares method.

5. Target Audience and Educational Uses

• Secondary and Junior College Students: The model is explicitly designed to be suitable for students at the secondary and junior college level, emphasizing concepts relevant to their curriculum.
• Curve Fitting and Data Analysis: The simulation promotes understanding of curve fitting, a fundamental process in data analysis and scientific modeling.
• Exploration of Mathematical Concepts: The interactive nature of the applet allows students to explore relationships between mathematical equations (polynomials) and their visual representations.
• Inquiry-Based Learning: By encouraging experimentation with parameters and comparison with the best-fit calculation, the simulation facilitates inquiry-based learning about mathematical modeling and curve fitting.

6. Credits and References

• Authors: Francisco Esquembre and Félix J. García Clemente
• Original Simulation: Francisco Esquembre and Miguel Marín López
• Reference: Least Squares entry on Wikipedia, used as a reference for the numerical methods applied.

7. Related Resources and Context The "Other Resources" section also provides context for the simulation by referencing a large number of other educational tools and simulations developed within the Open Educational Resources / Open Source Physics @ Singapore framework. These tools cover a diverse range of physics and mathematics topics. The list of popular tags also indicates popular learning topics.

8. Conclusion

The "Data Fitting JavaScript HTML5 Applet Simulation Model" is a valuable educational tool for teaching curve fitting and data analysis. Its interactive and user-friendly design, combined with its clear connection to underlying mathematical principles, makes it suitable for a wide range of educational settings. The use of open source libraries and an open license contributes to accessibility and adaptability for teachers and students. The model emphasizes interactive learning through its hands-on approach to data fitting, which aligns with modern pedagogical trends in STEM education.

Data Fitting Applet Study Guide

Quiz

1. What is the primary function of the Data Fitting JavaScript HTML5 Applet?
2. How can users add data points to the plotting panel within the applet?
3. What parameters can users adjust to fit a polynomial curve to the data?
4. What is the purpose of the "Best Fit" button within the simulation?
5. What is the role of the NumericJS model element within the applet?
6. What does the term "least squares approximation" refer to in the context of this applet?
7. According to the text, what is the goal when fitting a curve to data points in the simulation?
8. The text mentions an equation, y = f(x), what does f(x) represent?
9. How would you summarize the process for obtaining the best fit based on the provided information?
10. Where can one find additional information on the simulation’s model?

Quiz Answer Key

1. The primary function of the Data Fitting JavaScript HTML5 Applet is to allow users to fit a polynomial curve to a set of data points. It is used to visually represent the mathematical relationship between data.
2. Users can add data points to the plotting panel by clicking within the panel. Each click will add a data point up to a limit.
3. Users can adjust the parameters a, b, c, d, and e of the polynomial equation y = f(x) to fit the curve to the data. This allows users to customize the shape of the curve.
4. The "Best Fit" button calculates the best possible polynomial fit for the added data points by invoking a predefined method. This button shows how close to optimal the user’s manual fit is.
5. The NumericJS model element is used to solve the system of linear equations needed for the least squares approximation calculation in the simulation. It automates the more complex math process.
6. The "least squares approximation" refers to a mathematical method used to find the best fit curve for a set of data points by minimizing the sum of the squares of the differences between the observed and predicted values. This approach optimizes the accuracy of the fit.
7. The goal of fitting a curve to a number of points is to find the curve that best represents the data by adjusting parameters or even the function itself so the predicted values match the observed values as close as possible.
8. The f(x) represents a polynomial function of x. This function is designed to model the relationship between x and y, with the parameters a, b, c, d, and e determining its shape.
9. To obtain the best fit, one would begin by adding data points on the plotting panel. Then, they would adjust the parameters a, b, c, d, and e, or edit the computeBestFit() method, and click the "Best Fit" button to compare the user's fit to the optimal fit.
10. One can find additional information on the model, including the original simulation source and other related simulations, by following the links under the ‘Version’ section and the ‘Other Resources’ section of the document.

Essay Questions

1. Discuss the educational value of using an interactive simulation like the Data Fitting Applet for teaching mathematical concepts such as function fitting and least squares approximation.
2. Analyze the role of user interaction in the Data Fitting Applet and how it can enhance a student's understanding of the relationship between data and mathematical models.
3. Explain the significance of the "least squares approximation" method in the context of data analysis, and describe how the NumericJS element is essential to implement it.
4. Compare and contrast the process of manually fitting a curve to data points versus using the "Best Fit" button in the applet. What skills are involved in each approach?
5. Describe a scenario (outside of pure mathematics) where the principles of the Data Fitting Applet could be applied in a real-world context, and describe how the applet’s tools would facilitate that process.

Glossary of Key Terms

• Data Fitting: The process of finding a mathematical function that best represents a given set of data points. This involves adjusting parameters of a curve to minimize the discrepancy between the curve and the data.
• Polynomial Curve: A curve defined by a polynomial equation, such as y = ax + bx² + cx³... These curves can take a variety of shapes by adjusting their parameters.
• Parameters (a, b, c, d, e): The coefficients in a polynomial equation that determine the shape and position of the curve. Adjusting these allows users to modify the curve fit.
• Least Squares Approximation: A mathematical method used to find the best fit curve for a set of data points by minimizing the sum of the squares of the differences between the observed and predicted values. This method aims to minimize prediction errors.
• NumericJS: A JavaScript model element that performs the mathematical calculations needed to solve systems of linear equations. It automates the complexities of certain equations needed for the best fit.
• Basis of Linear Independent Functions: A set of functions (e.g. 1, x, x², x³) where no function in the set can be written as a linear combination of the other functions. This forms a basis that can fit any curve through a linear combination.
• Coefficients (cj): Numerical values that are multiplied by the linear independent functions in a mathematical expression or function. These help determine the size and shape of a curve.
• Best Fit Algorithm: A specific method used to determine the curve or function that most closely matches a given set of data points. This is usually the least squares approximation.
• Interactive Simulation: A computer-based model that allows users to manipulate variables and observe the effects on a system. This allows for exploration and learning by interaction.

Sample Learning Goals Procedure

This model fits a polynomial curve to a data set. Users can add points (up to a limit)  by clicking within the plotting panel. Add data to the panel and then adjust the parameters of the polynomial y = f(x), in order to obtain a good fit using the a,b,c,d, and e parameters. Use the best fit button to compare your fit to the the best possible polynomial fit.

NumericJS model element

This model demonstrates how to use theNumeric JSmodel element (see theElementspanel of the model) to solve the system of linear equations required for the least squares approximation.

Reference:Least Squaresentry of theWikipedia.

 

For Teachers Curve Data Fitting

The objective of this model is to fit a curve to a number of points. You can add points (up to a limit)  by clicking on the panel.

Your task is to adjust the parameters of the curve y = f(x), (or the functionf(x)itself!) in order to obtain the best possible fit. You have up to 5 parameters,a,b,c,d, and e.

Edit the "computeBestFit()" method in theCustompanel of the model to edit your best fit algorithm. Then, click on the "Best Fit" button, each time it is displayed in red, to invoke this method.

NumericJS model element

This model uses theNumeric JSmodel element (see theElementspanel of the model) to help you solve the system of linear equations required for the least squares approximation.

Reference: Least Squares entry of the Wikipedia.

Our function is

where{f_j(x)}are a basis of linear independent functions:{1,x,x²,x³,...,x^m}and{c_j}are the coefficients.

The objective is to minimize the sum:

.

To this end, we have to differentiate with respect toc_i, and equate to zero:

Obtaining the follow system:

where (a,b)_dare defined as:

.

Research

[text]

Video

[text]

 Version:

1. http://weelookang.blogspot.sg/2016/06/data-fitting-javascript-html5-applet.html
2. http://www.opensourcephysics.org/items/detail.cfm?ID=13350 original simulation by Francisco Esquembre and Miguel Marín López
   

Other Resources

[text]

FAQ

• What is the primary function of the Data Fitting JavaScript HTML5 Applet Simulation Model?
• This model allows users to fit a polynomial curve to a set of data points. Users can add points to a plotting panel by clicking, and then adjust the parameters of a polynomial equation (y = f(x), with up to 5 parameters: a, b, c, d, and e) to achieve the best fit for the data. This is useful for visualizing and understanding the relationship between variables in a dataset.
• How does the model determine the "best fit" for the data?
• The model uses a least squares approximation method to determine the best polynomial fit. This involves solving a system of linear equations using the Numeric JS model element. The "Best Fit" button invokes a method that calculates the optimal parameter values based on the least squares method, minimizing the sum of squared differences between the data points and the curve. Users can also manually adjust the parameters to better understand how each parameter affects the overall fit.
• What is the purpose of the "Numeric JS" model element in the simulation?
• The "Numeric JS" model element provides the functionality to solve systems of linear equations. In the context of this data fitting model, it's used to compute the coefficients (parameters a,b,c,d,e) of the best fit polynomial curve using the least squares approximation algorithm. This element handles the mathematical calculations involved.
• How can users add and manipulate data points within the simulation?
• Users can add data points to the simulation by clicking directly on the plotting panel. There is a limit to the number of points that can be added. These points can then be used as the basis for adjusting the polynomial fit to understand how the model relates to the data.
• Can the best fit algorithm be customized, and if so, how?
• Yes, the "computeBestFit()" method in the Custom panel of the model can be edited to customize the algorithm used to determine the best fit. This allows advanced users to implement different curve fitting techniques if desired. Users click the "Best Fit" button (which appears in red when the method is invoked) to execute their customized approach.
• What is the mathematical basis for the curve fitting implemented in the model?

The model uses a polynomial function of the form f(x) = c0*f0(x) + c1*f1(x)+ c2*f2(x) +....cm*fm(x) where {f(x)} are linearly independent functions, typically {1,x,x^2,x^3...} and {c} are coefficients to be found. The model aims to minimize the sum of the squares of the residuals, the difference between each observed y value and the predicted y value from f(x). This is achieved by differentiating this sum with respect to the coefficients, setting it to zero and solving the resulting system of linear equations for the coefficients.

• Is the simulation accessible on different devices, including mobile devices?
• Yes, the simulation is designed to be accessible on a wide range of devices, including desktops, laptops, and mobile devices such as smartphones and tablets. This accessibility is achieved by using HTML5 and JavaScript, which are widely supported by modern web browsers. This means that the model can be easily accessed on Android, iOS, Windows, MacOS, Linux, and Chromebook devices.
• Where can I find more information about the original simulation and its creators?
• The simulation was originally created by Francisco Esquembre and Miguel Marín López. Further information about the model, along with links to resources such as the original simulation and a blog post discussing it, can be found on the webpage. This includes links to the Open Source Physics website, which hosts a wide range of physics simulations and related resources. There is also a licensing section of the webpage that specifies the licensing for both the content and the Easy JavaScript Simulation library.