About

Mandelbrot - set

The members of the common Mandelbrot set follow the rule

z_n+1= z_n²+ c ; initial value z₀ = 0

c is a complex number, as is z

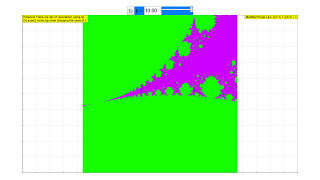
We look for points c in the complex plane, for which the series does not diverge. They form the Mandelbrot set. In the simulation they are colored red, lying within a range with the fractal boundary, the famous "apple man". Diverging points are colored green to blue, with the color shading indicating the speed of divergence.

Drawing a rectangle with the mouse defines a smaller range of calculation with correspondingly increasing resolution. Reset leads back to the initial condition.

Fractal for variable power law

The fractal character of the boundary of the Mandelbrot structure is a result of the nonlinearity of the series´ construction rule. It is not dependent on its specific square law rule.

To demonstrate this, a modified series is calculated with variable power law in the nonlinear term

z_n+1= z_n^k+ c; z₀ = 0; k≧ 1, a rational number

c is the complex number in the plane, for which convergence or divergence of the series is determined.

The calculation is more transparent when the complex number is written in polar coordinates.

z = x + i y = r (cosφ + i sinφ) = r e^iφ

r = √(x² + y²); φ = arctg (y / x)

z ^k = r ^k e^iφ = r ^k (cos (kφ) + i sin (kφ))

In the simulation a slider is used to vary the rational number k between 1 and 10. In the number field an arbitrary rational number can be input, for example an exact integer or a very high number such as 1000. k = 2 delivers the common "apple man" of the Mandelbrot set.

The default position when opening the simulation and after Reset is n = 10.

Be patient! This is a number crunching calculation, and it may take several seconds or even minutes to see the result after a change of k or after Reset, depending on the quality of your computer. When you assume that the computer has been hooked up, close the simulation and start it anew.

E1:Choose the power k = 2 and store the contour of the "apple man" in your memory.

E2: Choose a slightly different value of k and reflect how the change originates.

E3:  Type integers 1 to 10 into the text field. Watch for symmetries, study how they relate to k, and how the structure originates.

E4: Type a very high integer for k, e.g. 1000. The fractal looks close to a circle. Why? Take a look at the boundary several times magnified.

E5: Choose integer or rational k. Use the selection rectangle of the mouse to deeply intrude into the fractal, and look for especially attractive structures. Where are they? Why? (not an easy question).

mandelbrot xlm was originally developed by

Francisco Esquembre and Wolfgang Christian The variations were developed by Dieter Röß in October 2008

This simulation is part of

“Learning and Teaching Mathematics using Simulations

– Plus 2000 Examples from Physics”

ISBN 978-3-11-025005-3, Walter de Gruyter GmbH & Co. KG

 

Translations

Code	Language		Translator	Run

Credits

Dieter Roess - WEH- Foundation; Tan Wei Chiong; Loo Kang Wee; Francisco Esquembre ; Wolfgang Christian

Overview

This document provides a review of the "Mandelbrot Set (Variable Power) JavaScript Simulation Applet HTML5" resource available on the Open Educational Resources / Open Source Physics @ Singapore website. This resource offers an interactive simulation that allows users to explore a generalized form of the Mandelbrot set where the power in the iterative formula can be varied. The document outlines the key concepts presented, the functionality of the simulation, and its potential educational applications.

Main Themes and Important Ideas/Facts

1. The Standard Mandelbrot Set:

• The resource introduces the standard Mandelbrot set, defining it based on the iterative formula:
• "The members of the common Mandelbrot set follow the rule zn+1= zn2 + c ; initial value z0 = 0"
• Here, c and z are complex numbers.
• The Mandelbrot set consists of all complex numbers c for which this sequence does not diverge.
• In the simulation, points belonging to the Mandelbrot set are colored red and form the "famous 'apple man'" shape.
• Diverging points are colored green to blue, with the color indicating the speed of divergence.

2. Generalization to Variable Power Law (Multibrot Set):

• The resource highlights that the fractal nature of the Mandelbrot set's boundary arises from the nonlinearity of the iterative rule and is not exclusive to the square law.
• "The fractal character of the boundary of the Mandelbrot structure is a result of the nonlinearity of the series´ construction rule. It is not dependent on its specific square law rule."
• The simulation allows exploration of a modified series with a variable power law:
• "zn+1= znk + c ; z0 = 0; k≧ 1, a rational number"
• This generalized set is also referred to as the Multibrot Set.
• The power k can be a rational number greater than or equal to 1.

3. Representation in Polar Coordinates:

• The resource explains that the calculation becomes more transparent when complex numbers are represented in polar coordinates:
• "z = x + i y = r (cosφ + i sinφ) = r eiφ r = √(x2 + y2); φ = arctg (y / x) z k = r k eiφ = r k (cos (kφ) + i sin (kφ))"
• This representation facilitates the understanding of how raising a complex number to a power affects its magnitude and angle.

4. Simulation Functionality:

• The JavaScript simulation allows users to interact with the generalized Mandelbrot set.
• A slider enables the variation of the power k between 1 and 10.
• A number field allows for the input of arbitrary rational numbers for k, including integers and large values.
• Setting k = 2 reproduces the standard Mandelbrot set ("apple man").
• Drawing a rectangle with the mouse zooms into a smaller region, increasing the resolution.
• The Reset button returns the simulation to the initial conditions (default n = 10 for k upon opening and after reset, although this seems to be a typo and likely refers to the iteration limit, as the default k is stated later).
• The simulation requires computational resources, and users are advised to be patient as calculations, especially after changing k or resetting, can take time.

5. Experiments for Exploration:

• The resource suggests several experiments to guide user exploration:
• Comparing the k = 2 form with slightly different values.
• Observing symmetries when using integer values of k from 1 to 10.
• Investigating the shape for very high integer values of k (e.g., 1000), noting its resemblance to a circle and exploring magnified views.
• Finding "attractive structures" by zooming into the fractal for various integer or rational values of k.

6. Educational Applications:

• The simulation is presented as a tool for "Learning and Teaching Mathematics using Simulations."
• It provides a visual and interactive way to understand concepts related to:
• Sequences and series
• Complex numbers
• Fractals
• Nonlinear dynamics
• The variable power feature allows students to explore how changes in the underlying mathematical rule affect the resulting fractal structure.

7. Technical Details and Credits:

• The simulation was originally developed by Francisco Esquembre and Wolfgang Christian, with variations by Dieter Röß.
• It is part of the "Learning and Teaching Mathematics using Simulations" project.
• The resource acknowledges contributions from Dieter Roess, Tan Wei Chiong, Loo Kang Wee, Francisco Esquembre, and Wolfgang Christian.
• The simulation uses a specific coloring algorithm that currently limits the usability of negative powers, resulting in a monotone color page. This is noted as a known issue being addressed.
• "Disclaimer: Due to the colouring algorithm used, selecting negative powers will end up merely returning a monotone page of colour. We are currently working on implementing a better colouring algorithm for all our Mandelbrot Set simulations."
• The default value of k upon opening the simulation is set to k = 10.

8. Connection to Other Resources:

• The page includes a list of numerous other interactive resources available on the platform, spanning various topics in mathematics and physics. This suggests the simulation is part of a larger collection of educational tools.

Key Quotes

• "The members of the common Mandelbrot set follow the rule zn+1= zn2 + c ; initial value z0 = 0"
• "The fractal character of the boundary of the Mandelbrot structure is a result of the nonlinearity of the series´ construction rule. It is not dependent on its specific square law rule."
• "zn+1= znk + c ; z0 = 0; k≧ 1, a rational number"
• "k = 2 delivers the common 'apple man' of the Mandelbrot set."
• "This set is also called the Multibrot Set, as a portmanteau of 'Multiple' and 'Mandelbrot'."
• "Disclaimer: Due to the colouring algorithm used, selecting negative powers will end up merely returning a monotone page of colour."

Potential Educational Impact

This simulation offers a valuable tool for educators and students to visualize and explore the concept of the Mandelbrot set and its generalization. By allowing manipulation of the power in the defining equation, it can help students understand:

• The role of nonlinearity in generating complex structures like fractals.
• The connection between mathematical formulas and their visual representations.
• The concept of convergence and divergence in iterative processes.
• The properties of complex numbers and their representation.

The guided experiments encourage active learning and exploration of the mathematical landscape defined by the generalized Mandelbrot set. The interactive nature of the simulation can enhance engagement and provide a more intuitive understanding of these abstract mathematical concepts. However, educators should be aware of the computational demands of the simulation and the current limitation regarding negative powers.

Study Guide: Exploring the Variable Power Mandelbrot Set

Key Concepts

• Mandelbrot Set: The set of complex numbers c for which the iterated function zn+1 = zn2 + c, with initial value z0 = 0, does not diverge. These points form a fractal on the complex plane.
• Complex Number: A number of the form a + bi, where a and b are real numbers, and i is the imaginary unit (√-1). It can also be represented in polar coordinates as r(cos φ + i sin φ) = reiφ.
• Iteration: Repeated application of a function, using the output of one step as the input for the next. In the Mandelbrot set, the function znk + c is iterated.
• Divergence: In the context of the Mandelbrot set, a sequence of complex numbers diverges if the magnitude (absolute value) of the terms grows infinitely large as the iteration continues.
• Fractal: A geometric shape that exhibits self-similarity at different scales. Zooming into a fractal reveals smaller structures that are similar to the whole.
• Nonlinearity: A property of a system where the output is not directly proportional to the input. The zk term in the Mandelbrot iteration introduces nonlinearity, which is crucial for the fractal nature.
• Variable Power Law: The modification of the standard Mandelbrot iteration by replacing the exponent of 2 with a variable exponent k (zn+1 = znk + c).
• Multibrot Set: The generalization of the Mandelbrot set where the power in the iteration rule (zn+1 = znk + c) is a variable, denoted by k.
• Complex Plane: A plane where the horizontal axis represents the real part of a complex number and the vertical axis represents the imaginary part. Points in this plane can be associated with complex numbers.
• Polar Coordinates: A way to represent a complex number using its distance from the origin (r, the modulus) and the angle it makes with the positive real axis (φ, the argument).

Quiz

1. Describe the fundamental rule that determines membership in the standard Mandelbrot set. What are the initial conditions for the sequence zn?
2. What distinguishes the variable power Mandelbrot set (or Multibrot set) from the standard Mandelbrot set in terms of its iterative formula? What kind of values can the variable power k take in the provided simulation?
3. Explain the concept of divergence in the context of generating the Mandelbrot set. How is divergence visually represented in the simulation described in the source?
4. What is the significance of the nonlinearity in the series' construction rule for the Mandelbrot set's boundary? How does the variable power k affect this nonlinearity?
5. How are complex numbers represented in polar coordinates? Provide the formulas for the modulus (r) and the argument (φ) of a complex number z = x + iy.
6. What happens to the visual appearance of the Multibrot set in the simulation when a very high integer value is entered for the power k, such as 1000? Offer a brief explanation for this change.
7. Describe how users can explore different regions of the Mandelbrot set and increase the resolution of the generated image using the provided simulation.
8. What is the default value of the power k when the simulation is first opened or after the "Reset" button is clicked? What familiar shape is generated when k = 2?
9. According to the "Disclaimer," what limitation exists in the simulation regarding the selection of negative powers for k? What is the reason given for this limitation?
10. What is the relationship between the Mandelbrot set and the broader concept of fractals? Why is the boundary of the Mandelbrot set considered a fractal?

Quiz Answer Key

1. The standard Mandelbrot set consists of complex numbers c for which the sequence defined by zn+1 = zn2 + c does not diverge, starting with the initial value z0 = 0. Both c and z are complex numbers.
2. The variable power Mandelbrot set uses the iteration rule zn+1 = znk + c, where k is a variable power, instead of the fixed power of 2 in the standard set. In the simulation, k can be a rational number greater than or equal to 1, adjustable via a slider between 1 and 10 or by entering an arbitrary rational number.
3. Divergence in the Mandelbrot set context means that the magnitudes of the terms in the iterated sequence grow infinitely large. In the simulation, diverging points are colored green to blue, with the color shading indicating how quickly the sequence diverges.
4. The fractal character of the Mandelbrot set's boundary arises from the nonlinearity of the iteration rule. The variable power k directly influences the degree of this nonlinearity, leading to a variety of fractal shapes depending on the value of k.
5. A complex number z = x + iy in polar coordinates is represented as z = r(cos φ + i sin φ) = reiφ, where the modulus r is given by r = √(x2 + y2) and the argument φ is given by φ = arctg (y / x).
6. When a very high integer value for k (e.g., 1000) is used, the fractal in the simulation looks very close to a circle. This occurs because a high power causes zk to rapidly become very large or very small (close to zero) unless the magnitude of z is very close to 1, resulting in a near-circular boundary.
7. Users can explore different regions by drawing a rectangle with the mouse, which defines a smaller range of calculation with increased resolution. The "Reset" button returns the view to the initial conditions.
8. The default value of the power k when the simulation starts or after a reset is n = 10. When k = 2, the simulation generates the common "apple man" shape of the standard Mandelbrot set.
9. The coloring algorithm used in the simulation is not suitable for negative powers of k, which results in a monotone page of color. The developers are working on a better coloring algorithm to address this limitation.
10. The Mandelbrot set is a classic example of a fractal, exhibiting self-similarity and intricate details at different scales. Its boundary is a fractal because it possesses non-integer dimensions and its complexity persists no matter how much it is magnified.

Essay Format Questions

1. Discuss the role of nonlinearity in the generation of fractal patterns, using the variable power Mandelbrot set as a primary example. How does changing the power k in the iteration rule zn+1 = znk + c demonstrate the impact of nonlinearity on the resulting fractal structure?
2. Explain the process of iteration and divergence in the context of the Mandelbrot set. How are these mathematical concepts translated into the visual representation of the Mandelbrot and Multibrot sets in the provided JavaScript simulation?
3. Compare and contrast the standard Mandelbrot set (k=2) with Multibrot sets where k takes on different integer values (e.g., k=3, k=4, k=10). Based on the simulation experiments (E3), discuss the observed symmetries and the relationship between the value of k and the resulting fractal structure.
4. Analyze the effect of increasing the power k to very high values (as in experiment E4) on the shape of the Multibrot set. Using the concept of complex numbers and their properties under exponentiation, explain why the fractal approaches a circular form as k becomes large.
5. Considering the interactive nature of the JavaScript simulation, discuss the pedagogical value of such a tool for learning about complex numbers, iteration, divergence, and the concept of fractals. How do the experiments suggested in the source (E1-E5) contribute to a deeper understanding of the Mandelbrot and Multibrot sets?

Glossary of Key Terms

• Complex Conjugate: For a complex number z = a + bi, its complex conjugate is z̄ = a - bi.
• Complex Modulus (or Absolute Value): The distance of a complex number z = a + bi from the origin in the complex plane, calculated as |z| = √(a2 + b2), which is also equal to r in polar form.
• Convergence: In the context of an iterated sequence, convergence means that the terms of the sequence approach a finite limit as the number of iterations increases. The opposite of divergence.
• Domain Coloring: A technique for visualizing complex functions by assigning colors to points in the complex plane based on properties of the function's output at those points. The coloring in the Mandelbrot simulation is a form of domain coloring that indicates divergence speed.
• Rational Number: A number that can be expressed as a fraction p/q, where p and q are integers and q is not zero. The variable power k in the simulation can be any rational number k ≥ 1.

Sample Learning Goals

[text]

For Teachers

This is yet another variation of the Mandelbrot Set, the latest of the Mandelbrot series, you could say.

This time, what varies is the power to which the complex number z is raised to in each iteration.

The standard Mandelbrot Set is iterated as follows: z(n+1) = z(n)^2 + c

However, in this simulation, we define the algorithm as follows:

z(n+1) = z(n)^k + c, where k is a real number.

The value of k can be adjusted with either the slider, which allows the values to be set between 1 and 10, or with the field provided, which allows for any real value of k to be entered. This set is also called the Multibrot Set, as a portmanteau of "Multiple" and "Mandelbrot".

Disclaimer: Due to the colouring algorithm used, selecting negative powers will end up merely returning a monotone page of colour. We are currently working on implementing a better colouring algorithm for all our Mandelbrot Set simulations.
The default value of k is set to k = 10

Research

[text]

Video

[text]

 Version:

1. http://weelookang.blogspot.sg/2016/02/vector-addition-b-c-model-with.html improved version with joseph chua's inputs
2. http://weelookang.blogspot.sg/2014/10/vector-addition-model.html original simulation by lookang

Other Resources

[text]

Frequently Asked Questions: Mandelbrot Set (Variable Power) Simulation

1. What is the standard Mandelbrot set and how is it defined mathematically?

The standard Mandelbrot set is a collection of complex numbers, denoted as c, for which the iterative sequence defined by the rule zn+1 = zn2 + c, with the initial value z0 = 0, does not diverge (i.e., remains bounded) as n approaches infinity. Both c and z are complex numbers. Points c that satisfy this condition belong to the Mandelbrot set.

2. How does the "Mandelbrot Set with variable power law" simulation differ from the standard Mandelbrot set?

The key difference lies in the iterative rule used to generate the fractal. Instead of always squaring zn, this simulation allows for a variable power, k, in the nonlinear term. The iteration rule becomes zn+1 = znk + c, where k is a rational number greater than or equal to 1. This generalization is sometimes referred to as the Multibrot set.

3. How can the power k be adjusted in the simulation?

The simulation provides two ways to adjust the power k. A slider allows users to select values of k between 1 and 10. Additionally, a numerical input field enables users to enter any rational number for k, including integers and high values like 1000.

4. What visual changes occur when the power k is varied?

Changing the value of k significantly alters the shape and symmetries of the resulting fractal. For k = 2, the familiar "apple man" shape of the standard Mandelbrot set is produced. As k changes, different symmetries emerge, and the overall structure of the fractal evolves. For very high integer values of k, the fractal tends to resemble a circle.

5. Why does the fractal appear circular when k is a very high integer?

When k becomes very large, the term znk approaches zero very quickly unless the magnitude of zn is very close to 1. This is because if |zn| < 1, raising it to a large power makes it exceedingly small, and if |zn> 1, it grows very rapidly. Consequently, for the sequence to remain bounded, the magnitude of z must stay close to 1. This condition in the complex plane describes a circle of radius 1 centered at the origin, hence the circular appearance of the fractal for large k.

6. What do the different colors in the simulation represent?

In the simulation, points c that belong to the Mandelbrot set (i.e., the sequence does not diverge) are colored red and lie within the fractal boundary. Points c for which the sequence diverges are colored green to blue. The specific shade of green to blue indicates the speed at which the sequence diverges; faster divergence typically corresponds to different shades.

7. Can users explore different regions of the fractal in more detail?

Yes, the simulation allows users to define a smaller range of calculation by drawing a rectangle with the mouse. This action zooms into the selected region, correspondingly increasing the resolution and revealing finer details of the fractal structure. The "Reset" button returns the view to the initial conditions.

8. What is the significance of the nonlinearity in the series' construction rule for the fractal's boundary?

The fractal character of the Mandelbrot structure's boundary arises directly from the nonlinearity of the iterative rule (in the standard case, the squaring of zn, and in the generalized case, raising zn to the power of k). This nonlinearity leads to the intricate and self-similar patterns observed at different magnifications. The simulation with variable power k demonstrates that the fractal nature is not specific to the square law but is a general consequence of this type of nonlinear iteration in the complex plane.