About

The Burning Ship Fractal

The Burning Ship fractal consists of points, c, in the complex plane that obey the following rule

1. Start with the complex number z = a + ib where a and b are real numbers.
2. Generate a new complex number, z', by taking the absolute value of both the real and imaginary parts before squaring the resulting complex number, and adding the result to c. z' = (|Re(z)| + |Im(z)|*i)² + c.
3. Repeat steps 1 and 2. If the complex number z goes toward infinity, then the starting point, c, is not a member of the Mandelbrot set. All numbers that remain bounded are members of the set.

It can be shown that if the magnitude of z is greater than 2 , then z will approach infinity. The code assumes that the number c is in the set if |z| > 2 after 256 iterations. In order to show how rapidly a number fails the test, we color the pixel corresponding to the number of iterations.

Mandelbrot set with variable initial value

The members of the Mandelbrot set follow the rule

z_n+1= z_n²+ c ; initial value z₀ = 0

c is a complex number, as is z

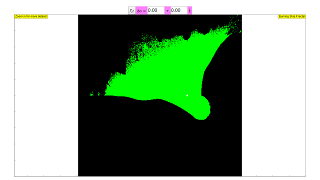
We look for points c in the complex plane, for which the series does not diverge. They form the Mandelbrot set. In the simulation they are colored red, lying within a range with the fractal boundary, the famous "apple man". Diverging points are colored green to blue, with the color shading indicating the speed of divergence.

Drawing a rectangle with the mouse defines a smaller range of calculation with correspondingly increasing resolution. Reset leads back to the initial condition.

The series has the members 0, c, c²+ c, c⁴ + 2c³ + c² + c,...

For deeper understanding this simulation modifies the series in such a way, that the initial z_o value is variable:

z₀ = real(z₀) + i * im(z₀) = k + i m

This series has the members z₀ , z₀²+c, ( z₀²+c)²+c, , ...

z₀ = 0 (k = 0 , m = 0) delivers the common Mandelbrot set, which is the default case for the simulation.

In the drawing z₀ corresponds to the white point, which can be drawn with the mouse. The fractal changes according to the change of the initial value. The values of the real and the imaginary part of z₀ are shown in two editable number fields. There one can input exact values (press the ENTER key after every change).

The fractal structure is caused by the nonlinearity of the series rule. It is observed for other nonlinear series as well, with different structure of the fractal.

mandelbrot.xlm was originally developed by Francisco Esquembre and Wolfgang Christian The variations were developed by Dieter Roess in October 2008

This simulation is part of

“Learning and Teaching Mathematics using Simulations

– Plus 2000 Examples from Physics”

ISBN 978-3-11-025005-3, Walter de Gruyter GmbH & Co. KG

 

Translations

Code	Language		Translator	Run

Credits

Dieter Roess - WEH- Foundation; Tan Wei Chiong; Loo Kang Wee; Francisco Esquembre; Wolfgang Christian

Overview:

This briefing document reviews the key information presented on the Open Educational Resources / Open Source Physics @ Singapore website concerning their JavaScript simulation applet for the Burning Ship fractal. The document outlines the fractal's definition, its relation to the Mandelbrot set, the functionalities of the provided simulation, and its educational context.

Main Themes and Important Ideas/Facts:

1. Definition of the Burning Ship Fractal:

• The Burning Ship fractal is defined based on an iterative process applied to points (c) in the complex plane.
• The iteration rule involves a complex number z = a + ib. A new complex number z' is generated by taking the absolute value of both the real and imaginary parts of z, squaring the result, and adding c: "**z' = (|Re(z)| + |Im(z)|*i)2 + c *."
• The iteration starts with an initial z (implicitly, this is the z from the previous step, and the process begins to determine if a given c belongs to the set).
• A point c belongs to the Burning Ship fractal if the magnitude of z remains bounded after repeated iterations. If |z| > 2 during the iteration, it is known that z will approach infinity, and therefore c is not a member of the set.
• The provided code in the simulation iterates up to 256 times to determine if |z| > 2.

1. Relationship to the Mandelbrot Set:

• The Burning Ship fractal is described as "a slight modification to the Mandelbrot Set".
• The key difference lies in the iteration rule. The Mandelbrot set uses the rule zn+1 = zn2 + c with an initial value z0 = 0.
• The Burning Ship fractal introduces the absolute value operation on the real and imaginary parts of z before squaring.
• The source emphasizes that "While this may seem like a small change to the equation, the change to the fractal itself is anything but." This suggests that the visual and mathematical properties of the Burning Ship fractal are significantly different from the Mandelbrot set.

1. Functionality of the JavaScript Simulation Applet:

• The webpage provides an embedded HTML5 JavaScript simulation applet of the Burning Ship fractal using an <iframe>.
• The simulation allows users to explore the fractal visually.
• It colors pixels based on the number of iterations it takes for the magnitude of z to exceed 2. This visualization shows how rapidly points diverge.
• Users can draw a rectangle with the mouse to define a smaller region of the complex plane, which the simulation will then calculate with "correspondingly increasing resolution."
• A "Reset" button returns the view to the initial conditions.

1. Extension: Mandelbrot Set with Variable Initial Value:

• The simulation also includes an extension that allows for exploring the Mandelbrot set with a variable initial value z0 = k + im.
• The standard Mandelbrot set is a specific case of this extension where z0 = 0 (k = 0, m = 0).
• The simulation colors points belonging to the standard Mandelbrot set (with z0 = 0) red.
• Diverging points in the standard Mandelbrot set are colored green to blue, with the shading indicating the speed of divergence.
• In this extended mode, a white point can be drawn with the mouse, representing the variable z0. The fractal image changes dynamically based on the value of z0.
• Editable number fields are provided to input exact values for the real (k) and imaginary (m) parts of z0.

1. Educational Context and Authorship:

• The simulation is presented as an "Open Educational Resource" and is part of the project "Learning and Teaching Mathematics using Simulations – Plus 2000 Examples from Physics."
• The original Mandelbrot set simulation (mandelbrot.xlm) was developed by Francisco Esquembre and Wolfgang Christian.
• The variations, including the Burning Ship fractal and the Mandelbrot set with variable initial value, were developed by Dieter Roess in October 2008.
• The simulation is intended for learning and teaching mathematics, particularly concepts related to sequences and series, and the visual representation of complex mathematical rules.
• The fractal structure itself is attributed to the "nonlinearity of the series rule."

1. Licensing and Credits:

• The contents of the webpage are licensed under the Creative Commons Attribution-Share Alike 4.0 Singapore License.
• Commercial use of the EasyJavaScriptSimulations Library (which likely powers the applet) requires a separate license from the University of Murcia (um.es).
• Credits are given to Dieter Roess, Tan Wei Chiong, Loo Kang Wee, Francisco Esquembre, and Wolfgang Christian for their contributions.

1. Related Resources:

• The webpage includes links to improved and original versions of a "Vector Addition" model, suggesting a broader scope of educational simulations available on the platform.
• A long list of other JavaScript Simulation Applets HTML5 is provided, covering a wide range of topics in mathematics and physics, indicating a rich collection of interactive learning tools.

Quotes:

• Burning Ship Fractal Definition: "The Burning Ship fractal consists of points, c , in the complex plane that obey the following rule... z' = (|Re(z)| + |Im(z)|*i)2 + c ."
• Divergence Criterion: "It can be shown that if the magnitude of z is greater than 2 , then z will approach infinity."
• Mandelbrot Set Rule: "zn+1= zn2 + c ; initial value z0 = 0"
• Burning Ship as a Modification: "The Burning Ship fractal is actually a slight modification to the Mandelbrot Set by taking the absolute value of both the real and imaginary parts of the complex number z before squaring it in each iteration."
• Impact of Modification: "While this may seem like a small change to the equation, the change to the fractal itself is anything but."
• Variable Initial Value: "For deeper understanding this simulation modifies the series in such a way, that the initial zo value is variable: z0 = real(z0) + i * im(z0 ) = k + i m"
• Fractal Structure: "The fractal structure is caused by the nonlinearity of the series rule."

Conclusion:

The provided source offers a JavaScript simulation applet for the Burning Ship fractal, a fascinating variation of the Mandelbrot set. The applet allows users to interactively explore this complex mathematical object and understand its generation through an iterative process involving complex numbers and absolute values. Additionally, the inclusion of a variable initial value for the Mandelbrot set provides a deeper insight into the dynamics of these fractal structures. The resource is clearly positioned within an educational context, aiming to enhance the learning and teaching of mathematics through interactive simulations, and is part of a larger collection of open educational resources in physics and mathematics.

 

Burning Ship Fractal Study Guide

Key Concepts:

• Complex Numbers: Numbers of the form a + bi, where a is the real part and b is the imaginary part, and i is the imaginary unit (√-1).
• Iteration: The repeated application of a process or rule. In the context of fractals, this involves repeatedly calculating a value based on the previous result.
• Fractal: A self-similar pattern that repeats at different scales. Fractals often exhibit infinite detail.
• Bounded Sequence: A sequence whose terms are all within some finite range; they do not approach infinity.
• Divergent Sequence: A sequence whose terms grow indefinitely large (approach infinity).
• Complex Plane: A two-dimensional plane where the horizontal axis represents the real part of a complex number and the vertical axis represents the imaginary part.
• Magnitude of a Complex Number (|z|): For a complex number z = a + bi, its magnitude is given by √(a² + b²).
• Burning Ship Fractal: A specific fractal defined by an iterative formula involving the absolute values of the real and imaginary parts of a complex number before squaring.
• Mandelbrot Set: Another famous fractal defined by a different iterative formula. The document highlights the Burning Ship fractal as a modification of the Mandelbrot set.
• Initial Value (z₀): The starting value used in the iterative process. The document discusses how varying this initial value can alter the fractal.

Quiz:

1. What is the fundamental difference in the iterative formula between the Mandelbrot set and the Burning Ship fractal, as described in the text?
2. Explain the process by which a point in the complex plane is determined to be part of the Burning Ship fractal according to the provided rules.
3. What criterion is used in the simulation code to determine if a complex number z will approach infinity, and after how many iterations does the code make this assumption?
4. How are points that are members of the Mandelbrot set and points that diverge colored differently in the described simulation?
5. What happens to the resolution of the fractal calculation when a rectangle is drawn with the mouse in the simulation?
6. Explain how the simulation allows for the exploration of the Mandelbrot set with a variable initial value, z₀.
7. According to the text, what mathematical property is identified as the underlying cause of the intricate fractal structures observed?
8. Who are credited as the original developers of the mandelbrot.xlm code and who developed the variations discussed in the text?
9. What is the significance of the threshold magnitude of 2 in the context of determining whether a complex number will tend towards infinity in these fractal calculations?
10. How does the Burning Ship fractal relate to the Mandelbrot set, according to the "For Teachers" section of the text?

Quiz Answer Key:

1. The key difference lies in the generation of the new complex number z'. For the Burning Ship fractal, the absolute value of both the real and imaginary parts of z are taken before squaring, while the standard Mandelbrot set squares z directly.
2. A starting complex number c is taken. Then, an iterative process begins with an initial complex number z. In each iteration, a new z' is calculated by taking the absolute value of the real and imaginary parts of the previous z, squaring the result, and adding c. If the magnitude of z remains bounded (does not go towards infinity) after a certain number of iterations, then c is considered part of the Burning Ship fractal.
3. The code assumes that if the magnitude of z becomes greater than 2 at any point during the iteration, then z will approach infinity. This test is performed for a maximum of 256 iterations.
4. In the Mandelbrot set simulation described with a variable initial value, the points that do not diverge (members of the set) are colored red, while the diverging points are colored green to blue, with the shading indicating the speed of divergence.
5. Drawing a rectangle with the mouse defines a smaller region of the complex plane to be calculated. This results in a correspondingly increasing resolution of the fractal within that selected area.
6. The simulation allows users to modify the initial value z₀ (represented as k + im) through editable number fields or by clicking on a white point in the drawing. By changing z₀, users can observe how the fractal structure of the Mandelbrot set changes.
7. The text states that the fractal structure is caused by the nonlinearity of the series rule used in the iterative process. This nonlinearity leads to the complex and self-similar patterns observed in fractals.
8. Francisco Esquembre and Wolfgang Christian originally developed mandelbrot.xlm. Dieter Roess developed the variations discussed in the text in October 2008.
9. The threshold magnitude of 2 is significant because it can be mathematically shown that if the magnitude of z exceeds 2 during the iteration, the sequence will definitely tend towards infinity and the starting point c is not part of the fractal set.
10. The "For Teachers" section explicitly states that the Burning Ship fractal is a slight modification of the Mandelbrot Set, specifically by taking the absolute value of the real and imaginary parts of z before squaring in each iteration.

Essay Format Questions:

1. Discuss the role of iteration in the generation of the Burning Ship fractal and explain how the behavior of the iterated complex numbers determines whether a point belongs to the fractal.
2. Compare and contrast the defining iterative formulas of the Burning Ship fractal and the Mandelbrot set. Analyze how the seemingly small modification in the Burning Ship formula leads to significantly different visual characteristics in the resulting fractal.
3. Explain the concept of boundedness and divergence in the context of complex number sequences and discuss its importance in defining fractal sets like the Burning Ship and Mandelbrot sets.
4. Describe how the provided JavaScript simulation allows for interactive exploration of the Mandelbrot set with a variable initial value. Discuss the potential educational benefits of such a simulation for understanding the properties of fractals.
5. Based on the provided text, discuss the connection between nonlinear mathematical rules and the emergence of complex, self-similar structures like the Burning Ship fractal. Can you suggest other areas in mathematics or science where nonlinearity leads to similarly complex phenomena?

Glossary of Key Terms:

• Complex Number: A number that can be expressed in the form a + bi, where a and b are real numbers, and i is the imaginary unit defined as the square root of -1.
• Iteration: The process of repeating a set of instructions or a calculation multiple times, using the output of one cycle as the input for the next.
• Fractal: A geometric shape that exhibits self-similarity at different scales, meaning that parts of the shape look similar to the whole. Fractals often have non-integer dimensions.
• Bounded: In mathematics, a sequence or set is bounded if all its elements are within a certain finite range or limit.
• Divergent: In mathematics, a sequence is divergent if it does not converge to a finite limit; its terms may grow indefinitely large.
• Complex Plane: A graphical representation of complex numbers where the real part is plotted along the horizontal axis and the imaginary part is plotted along the vertical axis.
• Magnitude (of a complex number): The distance of a complex number from the origin of the complex plane, calculated as √(a² + b²) for a complex number a + bi.
• Burning Ship Fractal: A fractal generated by iteratively applying the function z' = (|Re(z)| + |Im(z)|i)² + c to a starting complex number z, where c is a point in the complex plane.
• Mandelbrot Set: A fractal defined as the set of complex numbers c for which the sequence zn+1 = zn² + c with z₀ = 0 does not diverge.
• Initial Value: The starting point or first term in a sequence or an iterative process. In the context of fractals, it is the value of z at the beginning of the iteration (often denoted as z₀).
• Nonlinearity: A property of a system or equation where the output is not directly proportional to the input. In the context of fractals, the squaring operation in the iterative formulas introduces nonlinearity.

Sample Learning Goals

[text]

For Teachers

The Burning Ship fractal is actually a slight modification to the Mandelbrot Set by taking the absolute value of both the real and imaginary parts of the complex number z before squaring it in each iteration.

Thus, the equation is as follows:

While this may seem like a small change to the equation, the change to the fractal itself is anything but.

Research

[text]

Video

[text]

 Version:

1. http://weelookang.blogspot.sg/2016/02/vector-addition-b-c-model-with.html improved version with joseph chua's inputs
2. http://weelookang.blogspot.sg/2014/10/vector-addition-model.html original simulation by lookang

Other Resources

[text]

What is the Burning Ship Fractal?

The Burning Ship fractal is a set of points in the complex plane determined by an iterative formula. For each complex number c, a sequence is generated starting with z = a + ib. In each iteration, a new complex number z' is calculated by taking the absolute value of the real and imaginary parts of z, squaring the result, and adding c: z' = (|Re(z)| + |Im(z)|i)² + c*. If the magnitude of z tends towards infinity after repeated iterations, then the initial point c is not part of the Burning Ship fractal. Points that remain bounded form the fractal.

How does the formula for the Burning Ship fractal differ from the Mandelbrot set?

The key difference lies in the step where a new complex number is generated. For the Mandelbrot set, the formula is z' = z² + c. For the Burning Ship fractal, before squaring, the absolute values of the real and imaginary parts of z are taken: z' = (|Re(z)| + |Im(z)|i)² + c*. This seemingly small modification in the formula leads to a significantly different and distinct fractal shape.

What determines if a point belongs to the Burning Ship fractal?

A starting complex number c belongs to the Burning Ship fractal if, when the iterative process z' = (|Re(z)| + |Im(z)|i)² + c* is applied repeatedly (starting with some initial z, though typically related to the iteration), the magnitude of z does not exceed a certain bound (often 2) after a large number of iterations. If the magnitude grows indefinitely, the point c is not part of the fractal.

How is the Burning Ship fractal visualized?

The Burning Ship fractal is visualized by assigning colors to points in the complex plane based on their behavior under the iterative formula. Points that remain bounded (likely members of the fractal) are often colored differently from those that diverge to infinity. Furthermore, the rate of divergence can be indicated by the color; for example, points that diverge quickly might have one color, while those that take longer to diverge have another, creating the intricate details seen in fractal images.

What is the significance of the number of iterations in determining fractal membership?

Since it's impossible to perform an infinite number of iterations computationally, a maximum number of iterations is set (e.g., 256 in the described code). If the magnitude of z exceeds a certain threshold (e.g., 2) before reaching this maximum, the point is considered to be diverging. If it remains below the threshold after the maximum iterations, it is assumed to be bounded and thus a member of the set (for practical visualization purposes). The number of iterations influences the level of detail visible in the fractal; more iterations can reveal finer structures.

How does the provided simulation allow for exploration of the Mandelbrot set?

The simulation includes functionality to explore the Mandelbrot set as well. It uses the standard Mandelbrot iteration: zn+1 = zn² + c, with an initial value of z0 = 0. Points c for which this series does not diverge are part of the Mandelbrot set. The simulation colors these bounded points red and diverging points green to blue, with the shading indicating the speed of divergence. Users can zoom into specific regions by drawing a rectangle, increasing the resolution in that area.

What is the effect of a variable initial value (z0) on the Mandelbrot set in the simulation?

The simulation allows users to modify the initial value z0 in the Mandelbrot iteration (zn+1 = zn² + c). The default z0 = 0 produces the standard Mandelbrot set. By changing the real (k) and imaginary (m) parts of z0 (z0 = k + im), the resulting fractal changes its appearance. The white point on the drawing corresponds to the current z0, which can be manipulated with the mouse or by entering exact values in editable number fields. This demonstrates how the initial conditions of a nonlinear series can significantly impact the structure of the generated fractal.

What broader concept do the Burning Ship and Mandelbrot fractals illustrate in mathematics?

Both the Burning Ship and Mandelbrot fractals are examples of complex dynamical systems and illustrate the concept of self-similarity and how simple, nonlinear rules applied iteratively can generate incredibly complex and beautiful patterns. They highlight the idea of a boundary (the fractal boundary) where small changes in initial conditions can lead to drastically different long-term behavior (bounded vs. unbounded). Furthermore, the exploration of these fractals demonstrates the power of computational methods in visualizing and understanding abstract mathematical concepts related to sequences and series in the complex plane.