Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits

 Fu-Kwun Hwang - Dept. of Physics, National Taiwan Normal Univ.; lookang
Fu-Kwun Hwang - Dept. of Physics, National Taiwan Normal Univ.; lookang
Briefing Document: ⚛️Three-State Radioactive Decay Simulation
1. Overview
This document summarizes the key features and concepts related to a JavaScript simulation applet designed to model three-stage radioactive decay. This simulation, created by Fu-Kwun Hwang and hosted on the Open Educational Resources / Open Source Physics @ Singapore platform, is intended for educational purposes, particularly for students learning about nuclear physics. It uses a visual model and mathematical equations to demonstrate how radioactive nuclei decay over time through intermediate states to reach a stable end product.
2. Core Concepts and Simulation Mechanics
- Three-State Decay: The simulation models a radioactive decay process that occurs in three distinct stages:
- Initial State (Red): The original, unstable radioactive nuclei are represented in red.
- Intermediate State (Blue): The initial nuclei decay into a second, often also unstable, intermediary form, represented in blue.
- Final Stable State (Grey): The intermediate nuclei decay into a final, stable state represented in grey.
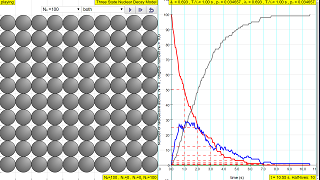
- The process is visually depicted, with the simulation showing the transformation of nuclei from red to blue to grey over time. The number of nuclei at each stage are tracked and graphed, allowing students to observe how each population changes.
- Half-Life: The simulation allows users to manipulate the half-life for each decay stage. This means one can adjust the time it takes for half of the nuclei in a given stage to decay into the next stage.
- The source specifies, "You can change decay half life time (unit: second) for each stage (from red-> blue -> grey)..." The half-life can be set from 0.1 to 3.0 seconds for each stage in the simulation.
- The source states, "The RED circles of this simulation symbolize 100 (variable selectable up 400 or 1024) to atomic nuclei of a radioactive substance whose half-life period (T11/2) amounts to 0.1 to 3.0 seconds." Thus the number of initial red nuclei is adjustable as well.
- Radioactive Decay Law: The simulation visually and mathematically demonstrates the radioactive decay law. The law states how the number of undecayed radioactive nuclei decreases over time. The simulation provides a graph that shows "the Number of radioactive atoms, N₁ not yet decayed nuclei at a given time t," which follows the equation:
- N₁ = N₀ * e^(-(ln2/T₁/₂) * t)
- where: * N₁ is the number of undecayed nuclei at time t * N₀ is the initial number of nuclei at time t=0 * T₁/₂ is the half-life of the decay
- Decay Rate (λ): The simulation uses decay rates, often denoted by the Greek letter lambda (λ), which is mathematically related to the half-life. The decay rate (λ) represents the probability of decay per unit time. The source states:
- "λ, or sometimes also known as 'lambda' the inverse of the mean lifetime, sometimes referred to as simply decay rate."
- "T 1/2 = ln(2)/λ"
- "( \lambda = \frac{p}{dt} )"
- Where "p is probability of decaying where 0 means no chance at all, 1 is 100% chance of decaying".
- Ordinary Differential Equations (ODEs): The core of the simulation is based on coupled ordinary differential equations that describe the changes in populations of nuclei at each stage:
- dN₁/dt = - λ₁N₁ (change in red nuclei)
- dN₂/dt = + λ₁N₁ - λ₂N₂ (change in blue nuclei)
- dN₃/dt = - λ₂N₂ (change in grey nuclei)
- Where: * λ₁ is the decay rate from red to blue * λ₂ is the decay rate from blue to grey.
3. Visualizations and User Interaction
- Interactive Model: The simulation uses an interactive model where users can manipulate key parameters, including the number of initial nuclei, and the half-lives for each stage.
- Graphical Representation: The simulation provides a real-time graph of the number of nuclei for each stage (red, blue, and grey) over time. This allows visual observation of the decay process and its exponential nature.
- Embeddable: The simulation is embeddable in webpages via an iframe, as shown with the example iframe code in the document, facilitating widespread use for educational purposes.
4. Intended Audience and Educational Context
- Educational Level: The simulation is primarily targeted towards junior college students and others studying nuclear physics and radioactive decay concepts. The source lists "Junior College" under the "tags" section.
- Learning Tool: The interactive nature of the simulation makes it an effective learning tool that can be used to help students:
- Visualize the radioactive decay process
- Understand the mathematical principles of radioactive decay
- Explore how half-life impacts decay rates
- Explore the effects of different decay constants on the system
5. Additional Resources The source includes links to: * A blogpost about the JavaScript version * A similar simulation with only two states * A Java version of this model * A Desmos Graphing Calculator visualization of decay graphs * Many other physics simulation and learning tools
6. Technical Details
- Technology: The simulation is built using JavaScript and HTML5, making it accessible on a wide range of devices including desktops, laptops, tablets, and smartphones.
- Open Source: This resource is part of the Open Educational Resources / Open Source Physics @ Singapore initiative. The source notes, "Contents are licensed Creative Commons Attribution-Share Alike 4.0 Singapore License".
- Platform: It utilizes the Easy JavaScript Simulation (EJS) framework. This framework appears several times in the source under tags and other linked resources.
7. Key Takeaways
This simulation is a valuable tool for understanding radioactive decay, particularly the complex process involving multiple decay stages. Its interactive nature and visual aids make it a practical resource for educators to teach and students to learn. By allowing manipulation of the half-lives and decay rates it highlights the role of these parameters on the decay process. The use of ODEs to model the changes in the nuclear population adds a layer of complexity and further highlights the physical processes at play.
Radioactive Decay Simulation Study Guide
Quiz
Instructions: Answer the following questions in 2-3 sentences each.
- In the simulation, what do the red, blue, and grey circles represent?
- What does the term "half-life" (T1/2) refer to in the context of radioactive decay?
- Explain what lambda (λ) represents in the simulation and how it relates to decay rate.
- What is the mathematical relationship between half-life (T1/2) and lambda (λ)?
- Describe the behavior of the red nuclei (N1) over time, according to the simulation's theory.
- What is the significance of the intermediate blue state (N2) in the three-state decay model?
- What do the coupled Ordinary Differential Equations (ODEs) describe in the context of this simulation?
- How does the simulation allow users to visualize the change in the number of different nuclei over time?
- Briefly explain the purpose of the graph on the right side of the simulation interface.
- How does the probability of decay (p) affect the decay rate?
Quiz Answer Key
- The red circles represent the original radioactive nuclei, the blue circles represent the intermediate, unstable daughter product, and the grey circles represent the final, stable granddaughter nuclei. These different colors allow for the visualization of the decay process from one state to the next.
- Half-life (T1/2) is the time it takes for the activity of a given amount of a radioactive substance to decay to half of its initial value. It is a fundamental characteristic that defines how quickly a radioactive substance decays.
- Lambda (λ) represents the decay rate, which is the inverse of the mean lifetime of a radioactive substance. It's often referred to as the probability of decay per unit time and is directly related to how quickly the substance decays.
- The relationship between half-life (T1/2) and lambda (λ) is given by the formula T1/2 = ln(2)/λ. This means that half-life is inversely proportional to the decay rate; a higher decay rate means a shorter half-life.
- According to the simulation's theory, the number of red nuclei (N1) decreases exponentially over time. This follows the radioactive decay law where the number of undecayed nuclei decreases at a rate proportional to their number.
- The intermediate blue state (N2) represents a daughter nucleus that is also unstable and radioactive, decaying further into the stable grey state (N3). This two-step decay is a key feature of the three-state model, showcasing successive radioactive transformations.
- The coupled Ordinary Differential Equations (ODEs) mathematically describe how the populations of the three different states of radioactive nuclei change over time. They show the rate of change for each population (N1, N2, and N3) related to their decay rates.
- The simulation allows users to visualize the change through color-coded traces, which are displayed on the graph on the right side. The colored lines track how the number of red, blue, and grey nuclei change over time.
- The graph on the right side shows the number of radioactive atoms versus time. The red trail represents the not-yet decayed nuclei (N1) over time, and visualizes the mathematical law for decay (N 1 = N 0 e -(ln2/T 1/2 ) ) t).
- The probability of decay (p) directly affects the decay rate (λ). A higher probability of decay per unit of time (p) results in a faster decay rate (λ) since the rate at which decay happens is proportional to p.
Essay Questions
Instructions: Answer the following questions in a well-structured essay format.
- Discuss how the three-state radioactive decay model is different from a simple two-state model, and explain why understanding this difference is important in nuclear physics.
- Using the simulation as a reference point, explain the relationship between half-life, decay rate, and the number of remaining radioactive nuclei, ensuring to integrate the mathematical formulas provided in the source material.
- Analyze the significance of the Ordinary Differential Equations (ODEs) in modeling radioactive decay. How do they accurately capture the behavior of the three-state system, and what insights do they provide?
- Compare and contrast the theoretical model presented in the simulation to real-world radioactive decay scenarios. Consider potential limitations and factors not explicitly addressed in the simulation.
- Explain how this simulation could be used as a tool for teaching radioactive decay concepts. Discuss its effectiveness, potential improvements, and broader pedagogical implications.
Glossary of Key Terms
- Radioactive Decay: The process by which an unstable atomic nucleus loses energy by emitting radiation in the form of particles or electromagnetic waves.
- Half-life (T1/2): The time required for half of the radioactive atoms in a sample to undergo radioactive decay.
- Decay Rate (λ): Also called the decay constant, this represents the probability of decay per unit time, characterizing how fast a radioactive substance decays.
- Ordinary Differential Equations (ODEs): Equations that describe the rate of change of a variable with respect to another, commonly time. In the context of this simulation, ODEs model changes in the populations of radioactive nuclei.
- Nuclei (plural of nucleus): The central part of an atom that contains protons and neutrons. Radioactive decay occurs within the nucleus.
- Daughter Nucleus: The nucleus resulting from the radioactive decay of a parent nucleus. It can itself be radioactive and undergo further decay.
- Granddaughter Nucleus: The nucleus resulting from the radioactive decay of a daughter nucleus. In this simulation, it represents the final, stable state after a two-step decay process.
- Exponential Decay: A pattern of decay where the rate of decrease is proportional to the current value, leading to a curve with the greatest change happening at the beginning.
- Probability of Decay (p): The likelihood that a single radioactive nucleus will decay within a given unit of time. It is related to the decay rate (λ) through the rate of change (dt).
- Three-State Decay: A radioactive decay process involving an initial radioactive nucleus, an intermediate radioactive daughter nucleus, and a final stable granddaughter nucleus.
Theory
The radioactive nuclei RED will decay into daughter product, and the daughter nucleus will decay grand-daughter stable nucleus.
The original nuclei are color code in Red
It will decay into blue-> grey (and become stable nuclei).
You can change decay half life time (unit: second) for each stage (from red-> blue -> grey),
click start and watch how the number of different nuclei changed with time -- colored traces.
The law of radioactive decay predicts how the number of the not decayed nuclei of a given radioactive substance decreases in the course of time. The RED circles of this simulation symbolize 100 (variable selectable up 400 or 1024) to atomic nuclei of a radioactive substance whose half-life period (T1 1/2) amounts to 0.1 to 3.0 seconds. However, in real life, sometimes these intermediate state N2 in BLUE are unstable themselves and are also radioactive whose half-life period (T2 1/2) amounts to 0.1 to 3.0 seconds, into the stable state N3 GREY.
The scientfic graph on the right, in number of radioactive atoms versus time, RED trail represents represents the Number of radioactive atoms, N₁ not yet decayed nuclei at a given time t, predicted by the following law:
N1 = N0 e -(ln2/T1/2)) t
when you play with the show model option, show me N1= No*exp(-ln(2)/T1/2*t)
the terms use are
N1 .... number of the not decayed nuclei
N2 .... number of the decayed nuclei
N0 ... number of the initially existing nuclei at time, t = 0
t .... time
T1/2 .... is the time taken for the activity of a given amount of a radioactive substance to decay to half of its initial value
λ, or sometimes also known as "lambda" the inverse of the mean lifetime, sometimes referred to as simply decay rate.
p is probability of decaying where 0 means no chance at all, 1 is 100% chance of decaying
Formula that related some of these terms are
T1/2 = ln(2)/λ
\( \lambda = \frac{p}{dt} \)
The Ordinary Differential equations used is
A three-state radioactive sample. Radionuclides change from red to green to blue as they decay. If the number of nuclides is large, the upper state N1, intermediate state N2, and final state N3 populations obey the following coupled ordinary differential equations (ODEs)
\( \frac{dN_{1}}{dt} = - \lambda_{1}N_{1} \)
\( \frac{dN_{2}}{dt} = + \lambda_{1}N_{1} - \lambda_{2}N_{2} \)
\( \frac{dN_{3}}{dt} = - \lambda_{2}N_{2} \)
where λ1 is the upper state decay rate and λ2 is the intermediate state decay rate. The nature of the decay is governed by these decay constants
Other Resources
- http://weelookang.blogspot.sg/2015/12/ejss-three-state-radioactive-decay-model.html lookang's Blogpost about the JavaScript version
- https://sg.iwant2study.org/ospsg/index.php/interactive-resources/physics/06-quantum-physics/02-nuclear/315-decaychangenwee by Fu-Kwun Hwang and lookang JavaScript version with only 2 states.
- http://www.opensourcephysics.org/items/detail.cfm?ID=10577 by Wolfgang Christian Java version similar in idea
- http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=194.0 by Fu-Kwun Hwang 2 state Java version
- https://www.desmos.com/calculator/kvs3p2selb Decay Graphs - Grand-Daughter- Grand child
Frequently Asked Questions: Three-State Radioactive Decay Simulation
- What does this simulation model demonstrate? This simulation models a three-stage radioactive decay process, where an initial radioactive substance (represented by red circles) decays into an intermediate unstable substance (blue circles), which subsequently decays into a stable substance (grey circles). The model allows users to visualize how the number of atoms of each type changes over time as well as understand the mathematical relationship for decay. The user is able to set the initial number of red atoms as well as control the half life of both decay stages.
- How do the colors in the simulation relate to the decay process? The red circles represent the original, unstable radioactive nuclei. These decay into blue circles, which represent the intermediate, also unstable daughter nuclei. The blue nuclei then decay into grey circles, which represent the final, stable grand-daughter nuclei. This visual color scheme allows you to track the progress of the decay chain.
- What parameters can be changed in the simulation? The simulation allows you to change the initial number of radioactive nuclei (N0), represented by the red circles, and the half-life (T1/2) for both the initial decay (red to blue) and the intermediate decay (blue to grey). The simulation can be restarted to begin with a different set of initial conditions.
- What is half-life (T1/2) and how does it affect the decay? Half-life is the time it takes for half of the radioactive nuclei in a sample to decay. The simulation uses different half-life values for each stage of the decay process, from red to blue to grey, and by changing these values, you can observe how quickly or slowly each stage progresses which influences how the graph of atoms vs time changes.
- What does the graph on the right side of the simulation represent? The scientific graph displays the number of radioactive atoms versus time. The red line depicts the number of original, not-yet-decayed nuclei (N1) at a given time, as predicted by the radioactive decay law. The graph illustrates the exponential decrease of these nuclei over time, demonstrating the relationship N1 = N0 * exp(-ln(2) / T1/2 * t), or in other words a direct correlation between the initial amount of a substance and the half life of a decay process, allowing for the ability to see the results of changes in these variables.
- What are the terms lambda (λ) and p (probability) and how do they relate to the decay process? Lambda (λ), also called the decay rate, is the inverse of the mean lifetime of a radioactive substance and represents the probability of decay per unit time. Probability (p) of decaying, represents the chance of a single nucleus decaying at any given time. In the equations provided, the decay rate is calculated by the formula (\lambda = \frac{p}{dt} ) and is directly related to the half life by the formula ( T_{1/2} = ln(2)/\lambda ). Lambda is important because it is directly related to the rate at which each decay occurs, where a higher lambda signifies a more rapid decay.
- What are the coupled ordinary differential equations (ODEs) used in the model? The simulation uses coupled ordinary differential equations to model the changing number of nuclei in each state over time:
- ( \frac{dN_{1}}{dt} = - \lambda_{1}N_{1} ) (describes the rate of change of red nuclei, N1)
- ( \frac{dN_{2}}{dt} = + \lambda_{1}N_{1} - \lambda_{2}N_{2} ) (describes the rate of change of blue nuclei, N2)
- ( \frac{dN_{3}}{dt} = - \lambda_{2}N_{2} ) (describes the rate of change of grey nuclei, N3)
- These equations consider the rate at which nuclei decay from one state to the next, where λ₁ and λ₂ represent the decay rates for the first (red to blue) and second (blue to grey) transitions, respectively.
- Where can I find additional resources related to this simulation? The following resources can provide further context or understanding to the simulation:
- A blog post by lookang about the JavaScript version of the simulation: http://weelookang.blogspot.sg/2015/12/ejss-three-state-radioactive-decay-model.html
- A two-state version of the JavaScript simulation by Fu-Kwun Hwang and lookang: https://sg.iwant2study.org/ospsg/index.php/interactive-resources/physics/06-quantum-physics/02-nuclear/315-decaychangenwee
- A Java version of the simulation by Wolfgang Christian: http://www.opensourcephysics.org/items/detail.cfm?ID=10577
- A two-state Java version by Fu-Kwun Hwang: http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=194.0
- Desmos graph showing decay graphs: https://www.desmos.com/calculator/kvs3p2selb
- Details
- Written by Loo Kang Wee
- Parent Category: 06 Modern Physics
- Category: 02 Nuclear
- Hits: 15341