About
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits

 Fu-Kwun Hwang - Dept. of Physics, National Taiwan Normal Univ.; lookang
Fu-Kwun Hwang - Dept. of Physics, National Taiwan Normal Univ.; lookang
Briefing Document: ⚛️Two-State Radioactive Decay JavaScript Simulation Applet
1. Overview:
This document reviews a JavaScript simulation applet designed by Fu-Kwun Hwang, hosted on the Open Educational Resources / Open Source Physics @ Singapore platform. The applet visually and numerically demonstrates the principles of radioactive decay, specifically focusing on a two-state decay process. It is intended for educational purposes, targeting secondary and junior college levels, and is accessible across various devices, including computers and mobile devices.
2. Key Concepts and Themes:
- Radioactive Decay: The simulation illustrates how the number of undecayed radioactive nuclei decreases over time. It emphasizes that this is a statistical process, governed by probability rather than a deterministic one.
- Half-Life (T1/2): A central concept, the simulation allows users to observe how the half-life affects the rate of decay. The half-life is defined as "the time taken for the activity of a given amount of a radioactive substance to decay to half of its initial value." The applet allows users to set a half-life period from 0.1 to 3.0 seconds.
- Mathematical Modeling: The simulation demonstrates the underlying mathematical equations governing radioactive decay, including exponential decay curves. The simulation uses the following equations, with N₁ representing the number of undecayed nuclei, N₂ representing the number of decayed nuclei, N₀ representing the initial number of nuclei, t representing time, and λ representing the decay constant:
- Undecayed Nuclei: N₁ = N₀ * e^-(ln2/T1/2)t
- Decayed Nuclei: N₂ = N₀ - N₀ * e^-(ln2/T1/2)t
- Rate of Decay: dN = pN₀ * e^-(ln2/T1/2)t
- Decay Rate (λ): The decay constant, λ, is introduced, which "is the inverse of the mean lifetime, sometimes referred to as simply decay rate," with the formula T1/2 = ln(2)/λ
- Probability of Decay (p): The simulation also incorporates the probability of decaying (p), which can range from 0 (no chance of decay) to 1 (100% chance of decay). The decay constant, λ, is defined as ( \lambda = \frac{p}{dt} )
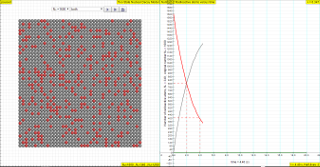
- Visual Representation: The applet uses grey circles to represent individual radioactive nuclei, providing a visual depiction of the decay process. These are not atoms, but a mathematical way of tracking change.
- Ordinary Differential Equations: The simulation uses ordinary differential equations to model the process, specifically ( \frac{dN_{1}}{dt} = - \lambda_{1}N_{1} )
3. Important Ideas and Facts:
- Simulation Parameters:
- The simulation begins with a user-selectable number of radioactive nuclei (up to 400 or 1024).
- The half-life can be adjusted from 0.1 to 3.0 seconds.
- The probability of decay, p, can also be modified to explore its effects on decay rate.
- Model Options: The simulation allows users to visualize the decay process by:
- Showing the number of undecayed atoms (N1) over time.
- Showing the number of decayed atoms (N2) over time.
- Showing the rate of radioactive atoms (dN) over time.
- Accessibility: The simulation is designed to work on a variety of platforms including desktops, laptops, tablets, and smartphones and provides an embedded iframe tag for website integration, enabling broader usage.
- Open Educational Resource: The resource is clearly identified as an Open Educational Resource, highlighting its availability for use and adaptation in educational settings, which means instructors can use this simulation with attribution under Creative Commons Attribution-Share Alike 4.0 Singapore License.
- Developer Credit: The applet is attributed to Fu-Kwun Hwang, with links to his other work and the original Java version, providing users with the source material information.
- Multiple Versions and Similar Models: The document provides links to similar simulation models including the original Java version, and a comparison of two HTML5 versions, as well as similar models from Wolfgang Christian and Walter Fendt, indicating the importance of this concept and the available resources for users.
- Additional Resources: The document provides a large list of other models available at the site, including more physics and math simulations along with examples of using the Tracker modeling software.
- Use of tracker: Tracker is an open source video analysis and modeling software used by this group for analysis of physics phenomena.
- Mathematical Formulas: Explicit mathematical formulas, such as those shown below, are given for both decayed and undecayed atoms.
- "N1 = N0 e -(ln2/T1/2) ) t"
- "N2 = N0 - N0 e -(ln2/T1/2) ) t"
- "dN = pN 0 e -(ln2/T1/2)) t"
4. Quotes from the Source:
- "The law of radioactive decay predicts how the number of the not decayed nuclei of a given radioactive substance decreases in the course of time."
- "The GREY circles of this simulation symbolize 100 (variable selectable up 400 or 1024) to atomic nuclei of a radioactive substance whose half-life period (T1/2) amounts to 0.1 to 3.0 seconds."
- "T1/2 .... is the time taken for the activity of a given amount of a radioactive substance to decay to half of its initial value."
- "λ, or sometimes also known as "lambda" the inverse of the mean lifetime, sometimes referred to as simply decay rate."
- "p is probability of decaying where 0 means no chance at all, 1 is 100% chance of decaying."
5. Conclusion:
This JavaScript simulation applet provides a valuable tool for teaching and learning about radioactive decay. Its interactive nature, combined with clear mathematical representations and visual aids, makes it an effective resource for understanding the key concepts and processes involved. The open educational resource nature of this simulation also allows it to be freely used, adapted, and shared within the educational community.
Radioactive Decay Study Guide
Quiz
Instructions: Answer the following questions in 2-3 sentences each.
- What do the grey circles represent in the simulation, and how many can there be?
- What does the half-life (T1/2) represent in the context of radioactive decay?
- Describe the meaning of N1 in the radioactive decay equations.
- What does N2 represent in the provided formulas, and how is it calculated?
- What is the significance of N0 in the context of the radioactive decay process?
- Explain the meaning of λ (lambda) in relation to radioactive decay.
- How does 'p' relate to the decay process?
- What relationship is described by the formula T1/2 = ln(2)/λ?
- Briefly explain the ordinary differential equation dN1/dt = -λ1N1.
- Where does the simulation come from and who created it?
Quiz Answer Key
- The grey circles in the simulation represent atomic nuclei of a radioactive substance. The number of these circles is variable and selectable from 100, 400 or 1024.
- Half-life (T1/2) is the time it takes for the activity of a radioactive substance to decay to half of its initial value. It's a characteristic constant for a particular radioactive isotope.
- N1 represents the number of radioactive atoms that have not yet decayed at a given time t. It decreases exponentially over time.
- N2 represents the number of radioactive atoms that have decayed at a given time. It's calculated by subtracting the current number of undecayed atoms (N1) from the initial number of atoms (N0).
- N0 represents the initial number of radioactive nuclei that exist at the beginning of the decay process, at time t = 0.
- Lambda (λ) represents the decay rate, sometimes referred to as the inverse of the mean lifetime of a radioactive substance. It indicates how quickly the substance is decaying.
- The variable 'p' represents the probability of a single nucleus decaying. It ranges from 0 (no chance of decay) to 1 (100% chance of decay).
- This formula indicates the inverse relationship between the half-life (T1/2) and decay rate (λ). A shorter half-life is associated with a higher decay rate.
- This differential equation states that the rate of change of the number of undecayed nuclei (dN1/dt) is directly proportional to the negative of the decay constant (λ1) and the current number of undecayed nuclei (N1).
- The simulation comes from Open Educational Resources / Open Source Physics @ Singapore and was designed by Fu-Kwun Hwang of the Dept. of Physics, National Taiwan Normal Univ.
Essay Questions
Instructions: Answer the following essay questions in well-structured paragraphs. Each response should demonstrate a clear understanding of the principles of radioactive decay.
- Explain how the radioactive decay simulation visually represents the exponential nature of radioactive decay. Discuss the relationship between the visual changes and the mathematical formulas provided.
- Compare and contrast the use of N1 and N2 in describing the process of radioactive decay. How do these variables change over time, and why are both needed to understand the full picture of decay?
- Discuss the factors that influence the rate of radioactive decay, and explain how the concepts of half-life and decay constant are related. Give examples of how changes in variables affect the decay rates.
- Describe how the simulation could be used as an educational tool to demonstrate and investigate the principles of radioactive decay to an audience unfamiliar with the concept. Detail the most important controls of the simulation, and their application.
- Explain the significance of the provided differential equation in the context of radioactive decay. How does this equation capture the dynamics of the process and what is the relationship to the formulas?
Glossary of Key Terms
- Radioactive Decay: The process by which an unstable atomic nucleus loses energy by emitting radiation, becoming a more stable nucleus.
- Half-life (T1/2): The time required for half of the radioactive nuclei in a sample to decay. It is a characteristic constant for a particular isotope.
- N1: The number of undecayed radioactive nuclei present at a given time (t).
- N2: The number of radioactive nuclei that have decayed at a given time (t).
- N0: The initial number of radioactive nuclei present at the start of the decay process (t=0).
- Decay Rate (λ or lambda): A constant that describes the probability of a single nucleus decaying per unit time. It can also be interpreted as the inverse of the mean lifetime of a radioactive substance.
- p: The probability of a single nucleus decaying. Ranges from 0 to 1, where 1 indicates 100% probability.
- Ordinary Differential Equation (ODE): A mathematical equation that relates a function with its derivatives and describes the change of that function over time.
Theory
The law of radioactive decay predicts how the number of the not decayed nuclei of a given radioactive substance decreases in the course of time. The GREY circles of this simulation symbolize 100 (variable selectable up 400 or 1024) to atomic nuclei of a radioactive substance whose half-life period (T1/2) amounts to 0.1 to 3.0 seconds. The scientfic graph on the right, in number of radioactive atoms versus time, RED trail represents represents the Number of radioactive atoms, N₁ not yet decayed nuclei at a given time t, predicted by the following law:
N1 = N0 e -(ln2/T1/2)) t
when you play with the show model option, show me N1= No*exp(-ln(2)/T1/2*t)
similarly it is possible to also predict the number of decayed atoms using the formula
N2 = N0 -N0 e -(ln2/T1/2)) t
when you play with the show model option, show me N2 = No-No*exp(-ln(2)/T1/2*t)
in the option both2 when selected, can display the rate of radioactive atoms versus time,
dN = pN0 e -(ln2/T1/2)) t
when you play with the show model option, show me dN = p*N0*exp(-ln(2)/T1/2*t)
the terms use are
N1 .... number of the not decayed nuclei
N2 .... number of the decayed nuclei
N0 ... number of the initially existing nuclei at time, t = 0
t .... time
T1/2 .... is the time taken for the activity of a given amount of a radioactive substance to decay to half of its initial value
λ, or sometimes also known as "lambda" the inverse of the mean lifetime, sometimes referred to as simply decay rate.
p is probability of decaying where 0 means no chance at all, 1 is 100% chance of decaying
Formula that related some of these terms are
T1/2 = ln(2)/λ
\( \lambda = \frac{p}{dt} \)
The Ordinary Differential equations used is
\( \frac{dN_{1}}{dt} = - \lambda_{1}N_{1} \)
Video
https://youtu.be/ekVI83tigEo?si=CeZKO-z4dV6XFPT8
Versions
- http://weelookang.blogspot.sg/2016/02/a-comparison-of-2-javascript-nuclear.html comparison of 2 HTML5 versions
- http://weelookang.blogspot.sg/2015/12/ejss-radioactive-decay-model.html lookang's blogpost about this JavaScript version
- http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=194.0 by Fu-Kwun Hwang original Java version
- http://www.opensourcephysics.org/items/detail.cfm?ID=10576 by Wolfgang Christian similar Java version
Other Resources
- http://www.opensourcephysics.org/items/detail.cfm?ID=13978&S=7 Two-State Nuclear Decay JS Model written by Wolfgang Christian
- http://www.walter-fendt.de/html5/phen/lawdecay_en.htm by Walter fendt
FAQ: Two-State Radioactive Decay Simulation
- What does this simulation demonstrate?
- This simulation visually and mathematically demonstrates the process of radioactive decay, specifically focusing on a two-state system. It models how the number of unstable atomic nuclei of a radioactive substance decreases over time, as they transform into a more stable state, using the principles of radioactive decay law. It showcases both the remaining undecayed nuclei and the accumulated decayed nuclei over time.
- What do the grey circles in the simulation represent?
- The grey circles in the simulation represent the initial number of atomic nuclei of a radioactive substance. The simulation allows the user to select an initial number from 100 up to 400 or 1024. Each circle graphically represents a single atom and its probability of decay.
- What is half-life (T₁/₂), and what is its role in this simulation?
- Half-life (T₁/₂) is the time it takes for half of the radioactive nuclei in a sample to decay. In the simulation, T₁/₂ is a user-adjustable parameter, ranging from 0.1 to 3.0 seconds, which influences how quickly the radioactive decay occurs. This allows users to observe how different half-lives affect the decay rate and the shape of the decay curve.
- What are N₁, N₂, and N₀ in the context of the simulation?
- N₁ represents the number of not yet decayed radioactive nuclei at a given time (t).
- N₂ represents the number of decayed nuclei at a given time (t).
- N₀ represents the number of radioactive nuclei present at the beginning of the simulation (at time t=0).
- What is the mathematical relationship governing the decay of radioactive nuclei in this simulation?
The number of undecayed nuclei (N₁) at a given time (t) is calculated using the formula:
* N₁ = N₀ * e^(-(ln2/T₁/₂) * t)
The number of decayed nuclei (N₂) is calculated using the formula: * N₂ = N₀ - N₀ * e^(-(ln2/T₁/₂) * t)
The rate of decay (dN) is calculated using the formula:
- dN = p * N₀ * e^(-(ln2/T₁/₂) * t)
Where:
* e is Euler's number (approx. 2.718)
* ln(2) is the natural logarithm of 2 (approx. 0.693)
* t is time
* p is the probability of decaying which ranges from 0 to 1
These formulas are based on the law of radioactive decay and allow us to model the exponential decrease in radioactive material over time.
- What is λ (lambda), also referred to as the decay rate and what is its relationship to half-life?
- λ (lambda) represents the decay constant or rate, which is the inverse of the mean lifetime of a radioactive substance. It determines how quickly the nuclei decay on average. The relationship between half-life (T₁/₂) and the decay constant (λ) is:
- T₁/₂ = ln(2) / λ or equivalently λ = ln(2) / T₁/₂
- What is the 'show model' option and what information does it display?
- The 'show model' option allows the user to overlay the mathematical models directly onto the graphical representation of the simulation. By doing so the user can observe a visual representation of the formulas that represent the decay. Specifically the exponential decay of the undecayed particles, the inverse exponential of the decayed particles, and the rate of decay over time can be shown.
- What can be learned from using this simulation?
- By using this simulation, one can develop a deeper understanding of radioactive decay, observe the exponential nature of decay, see the influence of half-life, understand the relationships between different variables such as N1, N2, No, and t, and see the relationship between differential equations and decay. It is also a visually rich and interactive way to understand concepts of exponential decay in science.
- Details
- Written by Loo Kang Wee
- Parent Category: 06 Modern Physics
- Category: 02 Nuclear
- Hits: 16194