About

Designed by Fu-Kwun Hwang http://www.phy.ntnu.edu.tw/ntnujava/ http://weelookang.blogspot.sg/2015/12/ejss-radioactive-decay-model.html  

Translations

Code	Language		Translator	Run

Credits

Fu-Kwun Hwang - Dept. of Physics, National Taiwan Normal Univ.; lookang; leongster

http://iwant2study.org/lookangejss/06QuantumPhysics_20nuclear/ejss_model_decaychangeNweedice/decaychangeNweedice_Simulation.xhtml

Theory

Assume the number of radioactive nucleus is N(t) --- not yet decayed into daughter product.
Each nucleus has the same probability p (p<1) decayed into daughter product.
It means that dN(t)/dt= -p*N(t) , where dN(t) is the number of nucleus decayed into daughter product at time t.
The solution is N(t)=N₀ e ^-pt = N0 e -(ln2/T_0.5)) t where N(0) is total number of nucleus at time t.

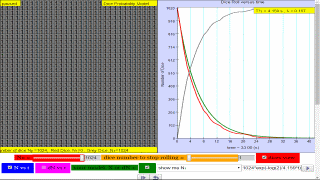
Each box represents a nucleus.
This applet lets you set the probability for a nucleus to decay and watch how the number of decayed nuclei (color changed to RED)  increased with time t.

YouTube

Other Resources

1. http://weelookang.blogspot.sg/2015/12/ejss-radioactive-decay-model.html lookang's blogpost about this JavaScript version
2. http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=194.0 by Fu-Kwun Hwang original Java version
3. http://www.opensourcephysics.org/items/detail.cfm?ID=10576 by Wolfgang Christian similar Java version

end faq

{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}