Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
| es | es | es |  |
|
Credits
![]()
 Wolfgang Christian - Davidson College; lookang
Wolfgang Christian - Davidson College; lookang
Briefing Doc: ⚛️Three-State Nuclear Decay Model
Source: "Three State Nuclear Decay JavaScript Model by Wolfgang Christian - Open Educational Resources / Open Source Physics @ Singapore"
Main Themes:
- Radioactive Decay: The model simulates the process of radioactive decay, where unstable atomic nuclei (radionuclides) transform into stable states.
- Three-State Decay: The simulation focuses on a specific scenario where the decay happens in two steps: an initial (parent) nucleus decays into an intermediate state before reaching a stable (final) state.
- Mathematical Modeling: The model utilizes both continuous differential equations and a stochastic (probabilistic) approach to represent the decay process.
Key Ideas/Facts:
- Decay Constants: Each decay step is governed by a constant decay rate (λ), reflecting the probability of decay per unit time.
- λ1 represents the decay rate from the parent nucleus to the intermediate state.
- λ2 represents the decay rate from the intermediate state to the stable state.
- Differential Equations: For large numbers of nuclides, the decay can be modeled using coupled ordinary differential equations:
- \(( \frac{dN_{1}}{dt} = - \lambda_{1}N_{1} ) ( \frac{dN_{2}}{dt} = + \lambda_{1}N_{1} - \lambda_{2}N_{2} ) ( \frac{dN_{3}}{dt} = - \lambda_{2}N_{2} )\)
- These equations describe the change in the number of nuclides (N) in each state over time (t).
- Stochastic Model: The simulation also employs a discrete model that considers the random nature of individual decay events.
- It calculates the probability of decay within a given time interval (Δt) for each nucleus.
- This approach highlights that the continuous model is an approximation, particularly for small numbers of nuclides.
- Direct Decay Probability: While nature doesn't skip the intermediate state, the model acknowledges the possibility of a parent nucleus decaying directly to the stable state within a given time interval. This occurs if the decay process is completed before the intermediate state can be observed.
- Interactive Simulation: The JavaScript model provides an interactive platform for visualizing the decay process. Users can manipulate parameters such as initial nuclide numbers, decay constants, and time intervals to explore the dynamics of three-state nuclear decay.
Quotes:
- "The simulation computes the probability of decay between states 1->2, 2->3, and 1->3 during the finite time interval Δt. When the simulation is run, these probabilities are applied to each radioactive nucleus to determine if it decays."
- "Note that there is a finite probability that a nuclide decays directly from state 1 to the stable state 3 within the time interval. Nature does not, however, skip state 2. We merely waited too long and the nuclide finished its decay before it was observed in state 2."
Significance: The model offers valuable insights into the fundamental processes of radioactive decay, demonstrating the interplay between deterministic and probabilistic approaches in scientific modeling. Its interactive nature makes it an effective tool for educational purposes, allowing users to engage with the concepts and explore the behavior of decaying systems
Three-State Nuclear Decay Model Study Guide
Short-Answer Questions
- Describe the process of three-state nuclear decay.
- What are the coupled ordinary differential equations (ODEs) that govern the populations of the three states in a radioactive sample undergoing three-state decay? Explain each term.
- Explain the difference between the continuous decay model and the discrete decay model. What are the limitations of the continuous model?
- What parameters can be adjusted in the Three State Nuclear Decay JavaScript Model before starting the simulation?
- What information is displayed in the plot of the Three State Nuclear Decay Model?
- How does the 'Radioactivity' checkbox change the view of the simulation?
- How does the 'Particles' checkbox affect the simulation view?
- Explain the significance of the decay constants λ1 and λ2 in the decay process.
- Why might a nuclide appear to decay directly from state 1 to state 3, even though it cannot skip state 2?
- What is the role of probability in the stochastic decay model?
Answer Key
- Three-state nuclear decay involves a radioactive parent nucleus decaying into an unstable intermediate nucleus, which then decays further into a stable daughter nucleus.
- The ODEs are: dN₁/dt = -λ₁N₁, dN₂/dt = +λ₁N₁ - λ₂N₂, and dN₃/dt = -λ₂N₂. N₁, N₂, and N₃ represent the number of nuclei in the parent, intermediate, and daughter states, respectively. λ₁ and λ₂ are the decay constants for the transitions from parent to intermediate and intermediate to daughter states.
- The continuous model uses differential equations to describe smooth decay curves, assuming a large number of nuclei. The discrete model acknowledges the random nature of decay, simulating individual decay events based on probability. The continuous model fails to represent the random fluctuations and discrete nature observed in small samples.
- Adjustable parameters include the initial number of parent and intermediate nuclei (N₁ and N₂), decay constants (k₁ and k₂), and the time interval between measurements (Δt).
- The plot displays the time evolution of the number of nuclei in each state (N₁, N₂, N₃) and can also show the number of decay events (ΔN₁, ΔN₂) within each time interval.
- The 'Radioactivity' checkbox switches the view to display the number of decay events (ΔN) within each time interval (Δt) instead of the total number of nuclei in each state.
- The 'Particles' checkbox enlarges the view of the sample, allowing for a better visualization of individual nuclei and their transitions between states.
- The decay constants λ₁ and λ₂ determine the probability of decay per unit time for the respective transitions. Higher decay constants indicate faster decay rates.
- A nuclide may appear to decay directly from state 1 to state 3 if the time interval between measurements (Δt) is longer than the time it takes for the nuclide to decay from state 1 to state 2 and then to state 3.
- In the stochastic model, probability is used to determine whether an individual nucleus decays within a given time interval. This introduces randomness into the simulation, reflecting the unpredictable nature of radioactive decay.
Essay Questions
- Discuss the limitations of both the continuous and discrete models of radioactive decay. In what situations is each model more appropriate?
- Explain how the Three State Nuclear Decay Model can be used to illustrate the concept of half-life. How would you determine the half-life of the parent and intermediate nuclides using the simulation?
- Describe how the decay constants λ1 and λ2 influence the shape of the decay curves for each state. What happens to the curves when λ1 is much larger than λ2, and vice versa?
- Compare and contrast the radioactive decay process with other physical phenomena that can be modeled using exponential functions. Discuss the similarities and differences in the mathematical representations and underlying principles.
- Explain how the Three State Nuclear Decay JavaScript Model could be used as an educational tool to teach students about radioactive decay. What are the advantages of using an interactive simulation in this context?
Glossary of Key Terms
Radioactive Decay: The spontaneous transformation of an unstable atomic nucleus into a more stable nucleus, releasing energy and/or particles in the process.
Nuclide: A specific type of atom characterized by its number of protons and neutrons.
Parent Nuclide: The initial unstable nuclide in a radioactive decay chain.
Daughter Nuclide: The stable nuclide resulting from the radioactive decay of the parent and any intermediate nuclides.
Intermediate Nuclide: An unstable nuclide formed as part of a decay chain, before the final stable daughter nuclide is produced.
Decay Constant (λ): A measure of the probability of a radioactive nucleus decaying per unit time.
Half-life: The time it takes for half of the radioactive nuclei in a sample to decay.
Continuous Decay Model: A mathematical model using differential equations to describe the smooth, continuous decline of the number of radioactive nuclei over time.
Discrete Decay Model: A model that simulates the decay of individual nuclei using probability, acknowledging the random and discrete nature of the process.
Stochastic: Involving random variables and probability.
ODE (Ordinary Differential Equation): A mathematical equation involving a function of one independent variable and its derivatives.
Δt: A small, finite time interval used in the simulation to calculate the number of decay events.
Three State Decay Theory
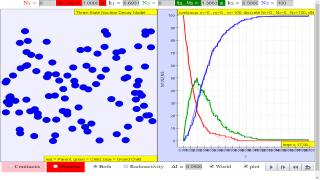
A three-state radioactive sample. Radionuclides change from red to green to blue as they decay. If the number of nuclides is large, the upper state N1, intermediate state N2, and final state N3 populations obey the following coupled ordinary differential equations (ODEs)
\( \frac{dN_{1}}{dt} = - \lambda_{1}N_{1} \)
\( \frac{dN_{2}}{dt} = + \lambda_{1}N_{1} - \lambda_{2}N_{2} \)
\( \frac{dN_{3}}{dt} = - \lambda_{2}N_{2} \)
where λ1 is the upper state decay rate and λ2 is the intermediate state decay rate. The nature of the decay is governed by these decay constants. The Three State Nuclear Decay Model displays both the continuous ODE solution for these nuclide populations as well as a stochastic (probabilistic) solution that assumes integer nuclide populations and uses probability to determine if a radionuclide survives for a time Δt without decaying.
Discrete decay model
The differential equation model produces continuous decay curves but hides the random and discrete nature of the underlying processes. A stochastic model that "rolls the dice" to determine if a radionuclide decays shows that the continuous model is only an approximation. The simulation computes the probably of decay between states 1->2, 2->3, and 1->3 during the finite time interval Δt. When the simulation is run, these probabilities are applied to each radioactive nucleus to determine if it decays. Note that there is a finite probability that a nuclide decays directly from state 1 to the stable state 3 within the time interval . Nature does not, however, skip state 2. We merely waited too long and the nuclide finished its decay before it was observed in state 2.
Introduction
The Three State Nuclear Decay JavaScript Model extends the Two State Nuclear Decay JavaScript Model to simulate the radioactive decay of atomic nuclei in which the parent nucleus first decays into an intermediate state before decaying into a stable state. Although the decay of both the parent and intermediate nucleus (radionuclides) is spontaneous and unpredictable, the probability of decay of each radionuclide is constant and is usually known. The model displays a color-coded sample with N1 parent nuclides, N2 intermediate state nuclides, and N3 stable state nuclides. Before the simulation starts, users can set the initial numbers N1 and N2, the decay constants k1 and k2, and the time interval between measurements Δt. The simulation counts the number of decay events ΔN1 and ΔN2 within Δt and stops when all nuclides are in the stable state.
The plot shows the time evolution of the nuclides as well as the number of decay events in each Δt time interval to allow users to compare the data generated by the random decay model with a differential equation-based model as described on the Theory page. The Radioactivity check box switches the view to show the number of decay events ΔN within the Δt interval as described on the Theory page. The Particles check box enlarges the nuclide view.
Credits:
The Three State Nuclear Decay model was developed by Wolfgang Christian using version 5.2 of the Easy Java/JavaScript Simulations (EjsS) authoring and modeling tool. Although EjsS is a Java program, it creates ready-to-run JavaScript simulations and ePubs. Information about EJS is available at: < http://www.um.es/fem/Ejs/> and in the OSP ComPADRE collection < http://www.compadre.org/OSP/>.
Version:
- http://weelookang.blogspot.sg/2011/01/ejs-open-source-decay-parent-daughter-g.html Blogpost remixing from Java to JavaScript by Loo Kang Wee
- http://www.compadre.org/osp/items/detail.cfm?ID=13991 by JavaScript Version by Wolfgang Christian
- http://www.compadre.org/osp/items/detail.cfm?ID=10577 by Java Version by Wolfgang Christian
Other Resources
[text]
Three State Nuclear Decay Model FAQ
What is the Three State Nuclear Decay Model?
This model simulates the radioactive decay of atomic nuclei where a parent nucleus decays into an intermediate state before reaching a stable state. It visually represents a sample with color-coded nuclei: red for the parent, green for the intermediate, and blue for the stable. The model allows for setting initial numbers of parent and intermediate nuclei (N1 and N2), decay constants (k1 and k2), and the time interval between measurements (Δt).
What are the two approaches to decay simulation in this model?
The model offers two simulation approaches:
- Continuous (ODE): This method uses coupled ordinary differential equations (ODEs) to describe the change in the number of nuclei over time, providing smooth decay curves.
- Stochastic (Probabilistic): This approach employs a probabilistic method, "rolling the dice" to decide whether individual nuclei decay within a given time interval. It highlights the random and discrete nature of radioactive decay.
What is the significance of the decay constants λ1 and λ2?
The decay constants λ1 and λ2 represent the probabilities of decay per unit time for the parent and intermediate states, respectively. They govern the speed and nature of the decay process. A higher decay constant indicates a faster decay rate.
Can a nuclide decay directly from state 1 to state 3?
While the model might show a direct decay from state 1 to state 3, it's crucial to understand that in reality, the decay process always goes through state 2. A direct jump simply means that the intermediate state was too short-lived to be observed within the chosen time interval Δt.
What information does the plot display?
The plot visually represents the evolution of the nuclide populations (N1, N2, and N3) over time. It also depicts the number of decay events (ΔN1 and ΔN2) within each time interval Δt. This allows for comparison between the continuous and stochastic models.
What is the purpose of the "Radioactivity" checkbox?
Selecting the "Radioactivity" checkbox changes the plot to display the number of decay events (ΔN) within each Δt interval instead of the total number of nuclei. This helps to understand the rate of decay events over time.
What does the "Particles" checkbox do?
The "Particles" checkbox provides a magnified view of the individual nuclides within the sample. This allows users to observe the color-coded nuclei and visually understand the decay process at a granular level.
Who developed the Three State Nuclear Decay Model?
The model was created by Wolfgang Christian using the Easy Java/JavaScript Simulations (EjsS) tool. It has undergone several revisions and translations, with contributions from Loo Kang Wee and others. It is hosted on the Open Educational Resources / Open Source Physics @ Singapore platform.
- Details
- Parent Category: 06 Modern Physics
- Category: 02 Nuclear
- Hits: 12024