Embed this model in a webpage:

<iframe width="100%" height="750" src="'.$fields["SIMU_EMBED"].'" frameborder="0"></iframe>

About

Briefing Document: ⚡EJS AC Generator 3D Model

1. Overview

This document reviews the "EJS AC Generator 3D Model" resource, an interactive simulation designed for educational purposes, particularly for secondary and junior college physics students. The simulation focuses on the principles of electromagnetic induction and how they are utilized in AC generators. It is part of the "Open Educational Resources / Open Source Physics @ Singapore" project. The simulation is built using Easy Java Simulation (EJS) and is accessible across various operating systems.

2. Core Concepts and Principles

• Electromagnetic Induction: The simulation centers on the fundamental principle of electromagnetic induction, specifically how motion within a magnetic field generates an electromotive force (EMF). It demonstrates how a changing magnetic flux through a coil induces an EMF, leading to the flow of current in a closed circuit.
• AC Generator Function: The simulation models a simple AC generator, comprising a rotating coil (armature or rotor) within a stationary magnetic field (stator). The rotation of the coil induces a time-varying EMF due to the changing magnetic flux experienced by the coil.
• Faraday's Law: The simulation's underlying principle is rooted in Faraday's Law, which is explicitly stated: "Faraday's law states the induced emf in a coil is equal to the negative of the rate of change of magnetic flux times the number of turns in the coil." The mathematical representation is given as |ε| = | d(Φ)/ dt | where Φ = N.B.A cos ( B&A).
• Lenz's Law: The document notes that Lenz's Law is also a key concept: "Lenz's law states an induced current is always in such a direction as to oppose the motion or change causing it." This law provides the physical interpretation of the negative sign in Faraday's Law, indicating that the induced emf and flux change have opposite directions.
• Motional EMF: The concept of motional EMF is explained: "The key to producing motional emf is in change in the magnetic flux experienced by the coil loop." The change in the magnetic flux is due to the rotation of the coil.
• Mathematical Derivation: The document provides a detailed derivation of the induced EMF for a rotating loop, starting from Faraday's law and using the trigonometric relationship to arrive at the formula for induced EMF: ε = N.B.A.ω .cos ( ω.t ).
• Relationship to Ohm's Law: The simulation connects the induced EMF to current flow through Ohm's law: "When a closed circuit in connected to the rotating loop, using Ohm's law ε = N.B.A.d( sin ( θ )/ dt ) = I.R"
• Right-Hand Rule The document mentions that when mechanical energy is used to rotate the loop, "the armature induced a emf described by the right hand rule." This is to help learners visualize the relationship between the direction of the movement of the coil in the magnetic field, and the direction of the induced current.

3. Simulation Features and Usage

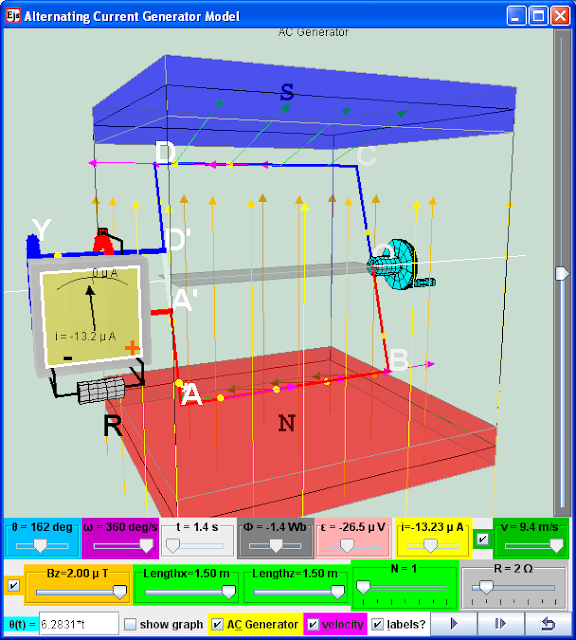
• Interactive 3D Model: The simulation features a 3D model of an AC generator. This allows students to visualize the different components (stator, armature, slip rings, brushes) and their interactions.
• Adjustable Parameters: The simulation offers various adjustable parameters, including:
• Magnetic Field Strength (Bz)
• Coil Dimensions (Lengthx, Lengthz)
• Number of turns in the coil (N)
• Resistance of the circuit (R)
• Angular displacement function θ(t)
• Visualizations: The simulation allows visualization of:
• Current flow and electron flow directions
• Graphs of EMF, current, and magnetic flux over time
• Interactive Exploration: The document encourages exploration through a series of guided questions and tasks, such as observing the effects of changing different parameters, collecting data to analyze the relationship between variables and to investigate the direction of forces in the AC generator.

4. Key Quotes

• "Electric generators turn motion into alternating-current electric power by exploiting electromagnetic induction."
• "The key to producing motional emf is in change in the magnetic flux experienced by the coil loop."
• "Faraday's law states the induced emf in a coil is equal to the negative of the rate of change of magnetic flux times the number of turns in the coil."
• "Lenz's law states an induced current is always in such a direction as to oppose the motion or change causing it."
• "When mechanical energy is used to rotate the loop, the armature induced a emf described by the right hand rule."
• "ε = N.B.A.ω .cos ( ω.t ) = I.R. which is the modeled equation"

5. Educational Value

• Conceptual Understanding: The simulation helps students visualize abstract concepts like electromagnetic induction and magnetic flux, thus promoting deeper understanding beyond just formula memorization.
• Hands-On Experience: The interactive nature of the simulation gives a more hands-on and engaging learning experience. Students can explore cause-and-effect relationships by adjusting parameters.
• Quantitative Analysis: The simulation encourages data collection and analysis, helping students make connections between the concepts, formulas, and graphical representations of the variables.
• Real-World Relevance: The simulation has an "Engage" section for teachers to discuss renewable energy sources, "to demonstrate a way to convert human mechanical energy in the form of rotating an axle to rotate a coil so as to get electrical energy", making the learning experience more practical and relevant.
• Problem-Solving and critical thinking: The simulation has an "Evaluate" section to guide learners towards collecting data to fill in a table to suggest relationships between variables. The simulation has an "Elaborate" section to guide learners to describe an AC generator, sketch a graph, and deduce directions of forces acting on the coil.

6. Teacher Support

• Guided Activities: The resource provides a section "For Teachers" with specific exercises and prompts, guiding the exploration of the simulation.
• Alternative Energy Discussion: The resource prompts a discussion on energy sources, relating the AC generator to real-world energy conversion.
• Advanced Exploration: The resource encourages advanced learners to create their own remix model and share it, fostering innovation and deeper learning.

7. Additional Points

• Software Requirements: The simulation requires Java to run, which may be a consideration for certain users.
• Credits: The resource gives credit to Fu Kwun Hwang and Loo Kang Wee for the development of the simulation.
• Open Source: The resource is part of an open educational resource initiative, making it freely available for educational purposes.
• Other Resources: The document includes links to other AC generator simulations, and several other educational models, broadening the learning experience and further exploring other physics concepts.

8. Conclusion

The EJS AC Generator 3D Model is a valuable educational tool for learning about electromagnetic induction and AC generators. Its interactive nature, adjustable parameters, and visualizations provide a hands-on, engaging, and effective learning experience. The simulation's focus on both conceptual and quantitative understanding, along with teacher support materials, makes it a useful tool for physics education.

AC Generator Study Guide

Quiz

Instructions: Answer the following questions in 2-3 sentences each.

1. What is the primary function of an AC generator?
2. Explain the concept of electromagnetic induction in the context of an AC generator.
3. What are the key components of a simple AC generator?
4. According to Faraday's law, how is the induced electromotive force (emf) related to magnetic flux?
5. State Lenz's Law and explain its significance in an AC generator.
6. How is the angle between the magnetic field and the area vector of the coil related to the induced emf?
7. Explain the relationship between angular velocity (ω) and the induced emf in a rotating coil.
8. What is the role of slip rings and brushes in an AC generator?
9. Describe how mechanical energy is converted to electrical energy in an AC generator.
10. What happens to the induced current when the coil is rotated faster?

Quiz Answer Key

1. An AC generator’s main function is to convert mechanical energy into electrical energy in the form of alternating current (AC). It does this by exploiting the principle of electromagnetic induction.
2. In an AC generator, electromagnetic induction occurs when a coil of wire rotates within a magnetic field. This motion causes a change in magnetic flux through the coil, which induces an electromotive force (emf), thereby generating electrical current.
3. The key components of a simple AC generator include a magnet (stator), a rotating coil of wire (armature or rotor), slip rings, and brushes. These components work together to convert mechanical motion into electrical energy.
4. Faraday's law states that the induced emf in a coil is equal to the negative rate of change of magnetic flux through the coil, multiplied by the number of turns. Essentially, the faster the magnetic flux changes, the greater the induced emf.
5. Lenz's law states that an induced current always flows in a direction that opposes the change causing it. In the context of an AC generator, the induced current generates a magnetic field that counteracts the changing magnetic flux, ensuring energy conservation.
6. The angle between the magnetic field and the area vector of the coil affects the magnetic flux. Specifically, the induced emf is directly proportional to the sine of the angle, meaning the emf is maximal when the field and the area vector are perpendicular.
7. The angular velocity (ω) is the rate at which the coil rotates. The induced emf is directly proportional to the angular velocity. A higher angular velocity leads to a more rapid change in magnetic flux and thus a larger induced emf.
8. Slip rings and brushes provide a continuous electrical connection between the rotating coil and the external circuit. The slip rings rotate with the coil, and the stationary brushes maintain contact to allow the current to flow.
9. Mechanical energy, often in the form of a rotating handle or turbine, rotates the coil within the magnetic field. As the coil rotates, the magnetic flux through the coil changes, inducing an emf, and thus converting mechanical energy into electrical energy.
10. When the coil is rotated faster, the rate of change of magnetic flux increases. This results in a higher induced emf and consequently, a greater induced current according to Ohm's law (I = ε/R).

Essay Questions

Instructions: Develop well-structured essays in response to the following prompts.

1. Discuss the significance of Faraday's Law and Lenz's Law in the operation of an AC generator. How do these principles dictate the production and direction of the induced current?
2. Analyze the various factors that influence the magnitude of the induced electromotive force (emf) in an AC generator. Specifically, discuss how changes in magnetic field strength, the area of the coil, and the angular velocity affect the output.
3. Compare and contrast the theoretical model of an AC generator with its practical application in a real-world scenario. How do practical considerations impact the design and performance of a real AC generator?
4. Explain how the interactive simulation provided in the source helps in understanding the principles of an AC generator. What insights can be gained by adjusting parameters within the simulation, such as the magnetic field strength and the angular velocity?
5. Evaluate the importance of AC generators as a means of producing electrical energy. Consider both the advantages and disadvantages of this technology as related to its global applications.

Glossary of Key Terms

• AC Generator: A device that converts mechanical energy into alternating current electrical energy using electromagnetic induction.
• Electromagnetic Induction: The process by which a changing magnetic field induces an electromotive force (emf) in a conductor.
• Electromotive Force (emf): The voltage generated by a changing magnetic field, which can drive a current in a closed circuit.
• Magnetic Flux: A measure of the total magnetic field passing through a given area. It's quantified by the number of magnetic field lines.
• Stator: The stationary part of a generator (or motor), typically containing magnets, which does not rotate during operation.
• Armature/Rotor: The rotating component of an AC generator, usually a coil of wire, that experiences changing magnetic flux, inducing the current.
• Slip Rings: Conducting rings that rotate with the armature, which maintain an electrical connection with the brushes in a generator.
• Brushes: Stationary contacts, usually made of carbon, that press against slip rings to conduct electricity to an external circuit.
• Faraday's Law: A law stating that the magnitude of the induced emf is directly proportional to the rate of change of magnetic flux through a coil.
• Lenz's Law: A law that states that the direction of an induced current is such that it opposes the change in magnetic flux that produced it.
• Angular Velocity (ω): The rate at which an object rotates, measured in radians per second.
• Motional emf: The electromotive force generated when a conductor moves through a magnetic field.

Electric generators turn motion into alternating-current electric power by exploiting electromagnetic induction. A loop that is placed in a magnetic field induces an motional electromagnetic force (emf). A simple alternating current (AC) generator is illustrated here. ABCD is mounted on an axle PQ. The ends of the wire of the loop are connected to 2 brushes contacting two slip rings continuously at position X & Y. Two carbon brushes are made to press lightly against the slip rings.

The motor features a external magnet (called the stator because it’s fixed in place) and an turning coil of wire called an armature ( rotor or coil, because it rotates). The armature induces an emf, because any change in the magnetic environment of a coil of wire will cause a voltage (emf) to be "induced" in the coil.

The key to producing motional emf is in change in the magnetic flux experienced by the coil loop.

Faraday's law states the induced emf in a coil is equal to the negative of the rate of change of magnetic flux times the number of turns in the coil. The induced electromotive force or emf, ε in any closed circuit is equal to the rate of change of the magnetic flux , Φ through the circuit.

|ε| = | d(Φ)/ dt  |

where Φ = N.B.A cos ( B&A)

|ε|  is the magnitude of the electromotive force (emf) in volts

Φ is the magnetic flux through the circuit (in webers).

N is the number of turns of wire in the loop
B is the magnetic field

A is area of coil

angle B&A is the angle between vector magnetic field and vector perpendicular to the area

Lenz's law states an induced current is always in such a direction as to oppose the motion or change causing it.
The law provides a physical interpretation of the choice of sign in Faraday's law of induction, indicating that the induced emf and the change in flux have opposite signs. The the polarity of the induced emf is such that it produces a current whose magnetic field opposes the change which produces it

ε = - d(Φ)/ dt

For the case of a rotating loop,

ε = - d(Φ)/ dt

From eariler equstion as Φ = N.B.A cos ( B&A)

ε = - d(N.B.A cos ( B&A))/ dt

the physical setup of Bz and normal vector of area A when t = 0 s, such that angle B&A = ( θ + π/2 ).
and taking out the constants from the differential equation,

ε = - N.B.A d( cos ( θ + π/2 )/ dt

from mathematical trigometry identity, cos ( θ + π/2) = -sin ( θ  )

ε = - N.B.A d( -sin ( θ  )/ dt

To derive an expression for the induced emf across the slip rings when the coil is spun at a angular frequency, ω, knowing θ = ω.t

ε = - N.B.A d( -sin ( ω.t  )/ dt )

ε = N.B.A d( sin ( θ )/ dt )     which the equation used by the custom function  getCurrent () = d( sin ( θ )/ dt )
When a closed ciruit in connected to the rotating loop, using Ohm's law

ε =  N.B.A.d( sin ( θ )/ dt ) = I.R      which the equation used by the model

When mechanical energy is used to rotate the loop, the armature induced a emf described by the right hand rule. The induced emf in a coil is equal to the negative of the rate of change of magnetic flux times the number of turns in the coil.

Use the rotating handle function input field θ(t)= _________ to see what happens when the rotating handle cranks the loop in the Bz magnetic field. The checkbox current flow & electron flow alows different visualization since I = d(Q)/dt and Q= number of charge*e. The Play & Pause button allows freezing the 3D view for visualizing these induced currents, for checking for consistency with the right hand rule.

When the rotating handle is moved by the input field θ(t)= 2*t , induced current runs through ABCD (select the checkbox labels?) in a manner described by
ε =  N.B.A.ω .cos ( ω.t  ) = I.R.

since θ(t)= 2*t , imply 2 = ω

ε/R =  N.B.A.ω .cos ( ω.t  )/R = I. which is the modeled equation.

If N = 1, B = 2 x10-6 T, A = 1.5*1.5 m*m, R = 1 Ω

ε/R =  1.2.1.5*1.5.2x10-6 .cos ( 2.t  )/1 = I.

ε = 9x10-6 cos ( 2.t  ) = I

For Teachers

Exercises:

Figure of a Real Life Demo Set by AddeStation Dr KC Tan

13 The external magnetic field Bz can be varied using the slider Bz. When Bz is positive, it is in the direction vertically up. Vary Bz until it is negative, what is the direction of the Bz then?

Lecture note on Ac Generator in JC

16.7 Simple Applications of EM Induction

16.7.1 A.C. Generators

Alternating current (a.c.) generators are devices that convert mechanical energy to electrical energy. In its simplest form, it consists of a loop of wire rotated by some external means in a magnetic field (as shown in the diagram below). In commercial power plants, the energy required to rotate the loop can be derived from a variety of sources (e.g. for hydroelectric plant, falling water is directed against the blades of a turbine to produce the rotary motion).

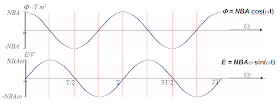
• The magnitude of the e.m.f. is given by:

If the coil is turning at a constant rate, then θ = ω.t where ω = the angular frequency.

Note: 
• The maximum magnitude of the e.m.f. is equal to when the coil is parallel to the field B ( vector A is 90 deg to notes θ) which in the applet case are angle θ = 0 and 180 deg but the notes θ = 90 and 270 deg 

Video

 by Ejs Open Source AC Generator Model Java Applet by lookang lawrence wee

 Ejs Open Source Alternating Current Generator Model Java Applet ( AC Generator ) v2011feb by lookang lawrence wee

 AC Generator by Michael Melloch

 How AC Generator Produces Electricity? - Physics || Extramarks

 Software Requirements

Java

Credits

Fu Kwun Hwang and Loo Kang Wee

Versions

1. http://iwant2study.org/lookangejss/05electricitynmagnetism_22electromagneticinduction/ejs/ejs_model_ACgenerator07.jarby Fu-Kwun Hwang and Loo Kang Wee Java version
2. http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=1275 by Fu-Kwun Hwang and Loo Kang Wee Java version
3. http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=915.0 by Fu-Kwun Hwang
4. http://www.compadre.org/OSP/items/detail.cfm?ID=9218&Attached=1 different Electric Generator Model by Anne Cox and Wolfgang Christian 

Other Resources

1. http://www.walter-fendt.de/ph14e/generator_e.htm by Generator Java version byWalter Fendt
2. http://micro.magnet.fsu.edu/electromag/java/generator/ac.html AC Generator Action Java version by National High Magnetic Field Laboratory.

FAQ: Understanding AC Generators

1. What is an AC generator and how does it work?
2. An AC (Alternating Current) generator is a device that converts mechanical energy into electrical energy in the form of alternating current. It achieves this through the principle of electromagnetic induction. A coil of wire (armature) is rotated within a magnetic field. This rotation causes a change in the magnetic flux experienced by the coil, which induces an electromotive force (emf) or voltage, which then drives the flow of current through a circuit connected to the generator. This means that mechanical motion generates electricity.
3. What is electromagnetic induction and how does it relate to an AC generator?
4. Electromagnetic induction is the process by which a changing magnetic field induces a voltage (emf) in a conductor, like a coil of wire. In an AC generator, the rotation of the armature in a magnetic field causes the magnetic flux (the amount of magnetic field passing through the coil) to change constantly. This change in flux induces an emf in the coil, which is the voltage that drives electric current. This is described by Faraday's Law.
5. What is magnetic flux, and why is its change important for an AC generator?
6. Magnetic flux (Φ) is a measure of the total magnetic field passing through a given area, such as a loop of wire. It's calculated by Φ = N.B.A cos ( B&A) where N is the number of turns of wire, B is magnetic field strength, A is the area of the coil, and the angle B&A is the angle between the magnetic field and a vector perpendicular to the area. In an AC generator, it's the change in magnetic flux, specifically how rapidly the flux is changing, which induces an emf. The changing flux is caused by the constant rotation of the coil in the magnetic field.
7. What is Faraday's Law, and how does it relate to the emf produced in an AC generator?
8. Faraday's Law states that the induced electromotive force (emf) in a closed circuit is equal to the negative rate of change of magnetic flux through the circuit. Mathematically, this is expressed as |ε| = |d(Φ)/dt|, where |ε| is the magnitude of the emf and |d(Φ)/dt| is the rate of change of magnetic flux. This means the faster the magnetic flux changes due to the rotation of the coil in the magnetic field, the larger the emf induced, resulting in a greater flow of current.
9. How do slip rings and brushes function in an AC generator?
10. The ends of the rotating wire loop in an AC generator are connected to slip rings. These slip rings rotate with the loop and maintain constant contact with stationary carbon brushes. The carbon brushes, in turn, are connected to the external circuit. This arrangement allows the generated current to flow to the external circuit without tangling the wires. They facilitate the transfer of electricity from the rotating components to the stationary external load.
11. What does Lenz's Law explain about the induced current in an AC generator?
12. Lenz's Law states that the induced current will always flow in a direction that opposes the change in magnetic flux that created it. This means that the magnetic field created by the induced current will oppose the motion of the coil, acting like a "brake". Lenz's Law clarifies why the negative sign appears in Faraday's Law, meaning the induced emf and the change in flux have opposite signs.
13. How does the rotation speed (angular frequency) of the coil affect the output of an AC generator?
14. The induced emf in an AC generator is directly proportional to the angular frequency (ω) of the coil's rotation, all other parameters being constant. The formula for the induced emf is given by ε = N.B.A.ω .cos ( ω.t ). A higher rotational speed means a higher rate of change of magnetic flux, resulting in a larger induced emf, and therefore a larger current. This also explains why the output of the generator is an alternating current (AC), where the polarity of the voltage oscillates as a sine or cosine wave corresponding to the rotation of the coil.
15. What factors affect the amount of emf induced by an AC generator?
16. The induced emf in an AC generator is directly influenced by several factors:

• Number of Turns (N): More turns of wire in the coil result in a higher induced emf.
• Magnetic Field Strength (B): A stronger magnetic field leads to a larger induced emf.
• Area of the Coil (A): A larger coil area increases the magnetic flux linkage and subsequently the induced emf.
• Angular Velocity (ω): As previously mentioned, the angular frequency of the rotation of the coil.

These factors, described by the formula: ε = N.B.A.ω .cos ( ω.t ), collectively define the magnitude and alternating nature of the electrical energy output.