Moment of Balancing Beam with Modelling Instruction approach by Boon Chien

Breadcrumbs

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.; Francisco Esquembre; Felix J. Garcia Clemente; concept by Boon Chien Yap

Older Version

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.; Francisco Esquembre; Felix J. Garcia Clemente; concept by Boon Chien Yap

Sample Learning Goals and SLS Lesson

understand the concept of moment of a force (torque)
relate moment of force as the product of force and perpendicular distance from the line of action of the force to a fixed point (pivot)
apply the establish Principle of Moment for body in static equilibrium

https://vle.learning.moe.edu.sg/my-library/lesson/view/20ceeafb-7a0c-49e6-b82d-0128b5bc18bb

For Teachers

Instruction for using the VLA for the various activities

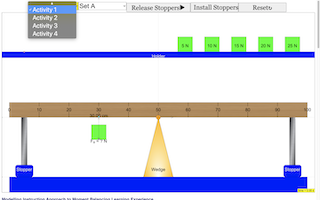
Please open the VLA on a new tab.
Select Activity
Select Set Number (if applicable)
Select the Release/Install Stoppers Button in between loading and unloading of the weights
Keep this tab open for the next few virtual experiments.

Activity 1: Moment Lab

MODEL DEVELOPMENT

Students engage in a scientifically oriented question.
Students collect, tabulate and analyse data from the investigation.
Students involved in evidence-based discussion through whiteboarding.

Turning Effect of a single weight

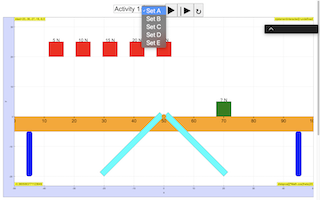
Look closely at the setup below. There is an unknown weight hanging on a ruler which is pivoted at its centre. The ruler is supported by two stoppers.

Observe what happen to the ruler in Figure 1 when the stoppers are released.

What caused the ruler to behave this way? Write down a possible Explanation below.

Answer: The metre ruler turns (anticlockwise), the left hand side side of the ruler with the unknown weight is nearer to the ground.

Procedure

Follow the on-screen instructions on the VLA. Try to balance the ruler with the different weights provided.
Record the values of the Force (F) and Distance (d) in the Google Sheet provided under your group number tab.
Plot a graph of F against 1/d. (The graph will be generated by the Google Sheet as the points are being tabulated.)
Discuss with your group members how to organise the data collected to support the findings from the group. (This process of collective thinking and collaboration is known as digital Whiteboarding)

Whiteboard Meeting on the Moment Lab

Model Development

Students formulates explanations from evidence
Students connects explanations to scientific knowledge
Students communicates and justifies explanations

Points of discussion for Whiteboard Meeting

Moment of force (from the gradient of the graph of F against 1/d )
identification of the correct pair of force and its corresponding perpendicular distance to the pivot, and the discussion points from the graphs
- Straight line graph
- Intercept may not be zero
- Units of axes
- Units of gradient and intercept
- At least two groups have the same values for gradient (and intercept); why?
- The rotation of the ruler due to the added weight (external force) is opposite to that given. In other words, one side the force tend to turn the ruler in clockwise direction and on the other side anticlockwise direction
- The value of the gradient (unit: Nm) is the same as the value of the given unknown weight x distance from the pivot.
- We give the name of this concept: Moment or Turning Effect of force or Torque
- In order for the ruler to be balanced, clockwise moment = anticlockwise momentprinciple of moment (the first condition for balance/equilibrium)

Research

[text]

Video

https://youtu.be/l2Udyp4ujBY Video Explanation by Mr Yap on Moment of Balancing Beam with Modelling Instruction approach

Version:

Other Resources

[text]

end faq

{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}