About

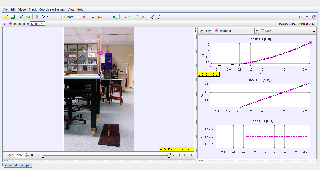
The 2 masses are 0.82g and 0.65g respectively. A model is created to show that the tensions are equal

For Teachers

- atwoodmachine.mp4

Credits

Author: Leong Tze Kwang

Document Brief: Title: "Atwood Machine Dynamics: A Tracker Model by Leong Tze Kwang"

This document explores the motion of an Atwood machine, analyzed using Tracker software. The study highlights key principles of classical mechanics such as tension, acceleration, and the interplay of forces within a two-mass pulley system.

Study Guide:

Objective:

• Analyze the dynamics of an Atwood machine.

• Use Tracker to measure and model the motion of the system.

Key Concepts:

1. Newton’s Second Law:

   • Net force = mass × acceleration (F = ma).

   • In the Atwood machine, the difference in gravitational force between two masses drives the motion.

2. Tension in the String:

   • The string transmits force between the masses and the pulley.

3. Acceleration of the System:

   • Determined by the net force and the total mass of the system.

4. Energy Conservation:

   • Potential and kinetic energy interchange during motion.

Experiment Setup:

• Materials:

  • Atwood machine setup (pulley, string, and two hanging masses).

  • High-speed camera or smartphone for video recording.

  • Tracker software for motion analysis.

• Procedure:

  1. Assemble the Atwood machine with known masses.

  2. Ensure the string and pulley system have minimal friction.

  3. Release the masses from rest and record their motion.

  4. Import the video into Tracker.

  5. Analyze displacement, velocity, and acceleration over time for each mass.

Expected Observations:

• Acceleration is constant for both masses.

• The lighter mass moves upward while the heavier mass moves downward.

• The magnitude of acceleration depends on the difference in mass and the system's total mass.

Questions to Consider:

1. What factors influence the acceleration of the system?

   • Answer: The difference between the gravitational forces acting on the two masses and the total mass of the system.

2. How does friction affect the results?

   • Answer: Friction reduces the net force, causing a lower acceleration than predicted by the ideal model.

3. What assumptions are made in this experiment?

   • Answer: Negligible string mass and pulley friction; constant gravitational force.

4. Can energy conservation be observed?

   • Answer: Yes, potential energy lost by the descending mass converts to kinetic energy and potential energy gain in the ascending mass.

5. How does changing the mass difference affect the motion?

   • Answer: Larger mass differences increase acceleration, while equal masses result in no motion.

FAQ:

1. Why study the Atwood machine?

   • It demonstrates foundational concepts in mechanics, including force, motion, and energy conservation.

2. How accurate is Tracker for this analysis?

   • Tracker provides precise measurements of displacement, velocity, and acceleration, allowing detailed analysis of motion.

3. What improvements can reduce experimental error?

   • Minimize friction, use a lightweight string, and ensure accurate mass measurements.

4. How does the pulley’s moment of inertia affect results?

   • If significant, the pulley’s rotational inertia must be accounted for in the equations of motion.

5. Can this model be extended?

   • Yes, by incorporating factors such as pulley friction, rotational inertia, or using a non-ideal string.

Would you like detailed equations for the system or guidance on extending this model?

I’m trying to teach the importance of relating to physical measurements in modelling.

As far as possible, we should try to make our model relate to real world measured data.

The mass of the slotted mass are 0.82 g and 0.65 g respectively.