Lissajous Curves JavaScript Simulation Applet HTML5

Breadcrumbs

About

Lissajous Figures Lissajous curves were studied by the French physicist and mathematician Jules Antoine Lissajous (1822 - 1880). Lissajous curves are the composition of two harmonic motions (sinusoids):

x = amplitude * cos ( frequency1 * time )
y = amplitude * cos ( frecuency2 * time + phase ) The shape of the curves are highly sensitive to the ratio frequency1/frequency2. Do experiment with different values of the frequencies and the phase using the fields provided in the simulation. Activities This virtual-lab will enable you to analyze the Lissajous figures. The view of the virtual-lab contains three buttons (A, B and C), which set predefined values to the frequency and the phase of the harmonic signals. In addition, the numerical values of the frequency and the phase can be selected by the lab's user. Authors Alfonso Urquía and Carla Martín
Dpto. de Informática y Automática
E.T.S. Ingeniería Informática, UNED
Juan del Rosal 16, 28040 Madrid, Spain

Translations

Code	Language		Translator	Run

Credits

Alfonso Urqua; Carla Martn; Tan Wei Chiong; Loo Kang Wee

1. Introduction:

This briefing document reviews the Lissajous Curves JavaScript Simulation Applet HTML5 provided by Open Educational Resources / Open Source Physics @ Singapore. This interactive resource is designed to help users understand Lissajous curves, their mathematical basis, and the impact of different parameters on their shape.

2. Main Themes and Important Ideas:

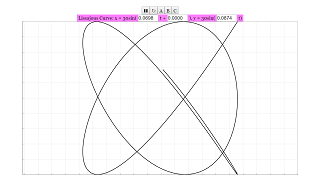
Definition of Lissajous Curves: The core theme is the introduction and exploration of Lissajous curves, which are defined as the result of the "composition of two harmonic motions (sinusoids)."
The source explicitly provides the parametric equations that define these curves:
x = amplitude * cos ( frequency1 * time )
y = amplitude * cos ( frecuency2 * time + phase )
Sensitivity to Frequency Ratio: A key idea highlighted is the significant influence of the ratio between the two frequencies (frequency1/frequency2) on the resulting shape of the Lissajous curve. The source states, "The shape of the curves are highly sensitive to the ratio frequency1/frequency2." This suggests that even small changes in the frequency ratio can lead to dramatically different visual outcomes.
Impact of Phase: The briefing also emphasizes the role of the "phase" parameter in shaping the Lissajous curves. The y equation includes a phase term, indicating that the relative starting points of the two sinusoidal motions affect the final figure.
Interactive Exploration: The resource is presented as a "virtual-lab" that encourages active learning through experimentation. Users can interact with the simulation by:
Using provided fields to adjust the numerical values of the frequencies and the phase.
Observing the immediate changes in the generated Lissajous curve as these parameters are modified.
Utilizing three predefined button options (A, B, and C) which set specific values for frequency and phase to showcase different curve examples.
Educational Purpose: The resource is clearly intended for educational purposes, falling under the categories of "Mathematics" and "Functions and graphs." It is listed within the "Open Educational Resources / Open Source Physics @ Singapore" framework, indicating a commitment to freely available learning materials. The "For Teachers" section explicitly states that "Lissajous curves are a family of parametric curves studied by the French physicist and mathematician Jules Antoine Lissajous (1822 - 1880)" and encourages experimentation to see how the graph changes with different parameter values.
Technical Implementation: The applet is implemented using JavaScript and HTML5, making it embeddable in web pages via an <iframe> tag. This allows for easy integration into online learning platforms or educational websites.
Attribution and Authorship: The source credits Alfonso Urquía and Carla Martín from the Dpto. de Informática y Automática, E.T.S. Ingeniería Informática, UNED (Madrid, Spain) as the authors of the simulation. Additional credits are given to Tan Wei Chiong and Loo Kang Wee.
Licensing: The content is licensed under the Creative Commons Attribution-Share Alike 4.0 Singapore License, promoting sharing and adaptation with proper attribution. Commercial use of the underlying EasyJavaScriptSimulations Library requires a separate license.
Context within the OER Platform: The applet is presented within a broader collection of interactive resources covering various topics in physics and mathematics, as evidenced by the extensive list of other simulations available on the website. This suggests a rich environment for exploring different scientific and mathematical concepts through interactive models.

3. Key Facts:

Lissajous Curves: Formed by the combination of two sinusoidal motions at right angles.
Historical Context: Studied by the French physicist and mathematician Jules Antoine Lissajous (1822 - 1880).
Mathematical Representation: Defined by the parametric equations:
x = amplitude * cos ( frequency1 * time )
y = amplitude * cos ( frecuency2 * time + phase )
Primary Influencers of Shape: The ratio of the two frequencies (frequency1/frequency2) and the phase difference are the primary determinants of the curve's shape.
Simulation Features: Allows users to manipulate frequency1, frecuency2, and phase through interactive fields and provides three preset configurations. The amplitude is fixed at 30 in this simulation.
Technology: Developed using JavaScript and HTML5 for web-based interactivity.
Authors: Alfonso Urquía and Carla Martín.
Platform: Hosted by Open Educational Resources / Open Source Physics @ Singapore.
Licensing: Creative Commons Attribution-Share Alike 4.0 Singapore License.

4. Quotes:

"Lissajous curves are the composition of two harmonic motions (sinusoids): x = amplitude * cos ( frequency1 * time ) y = amplitude * cos ( frecuency2 * time + phase )"
"The shape of the curves are highly sensitive to the ratio frequency1/frequency2."
"This virtual-lab will enable you to analyze the Lissajous figures. The view of the virtual-lab contains three buttons (A, B and C), which set predefined values to the frequency and the phase of the harmonic signals. In addition, the numerical values of the frequency and the phase can be selected by the lab's user."
"Do experiment with different values of the frequencies and the phase using the fields provided in the simulation, and see how the graph changes."

5. Conclusion:

The Lissajous Curves JavaScript Simulation Applet is a valuable open educational resource for understanding the generation and properties of Lissajous curves. Its interactive nature allows users to directly explore the influence of frequency ratios and phase differences on the resulting graphical figures. The clear mathematical definitions, coupled with the user-friendly interface, make this applet a useful tool for students and educators in mathematics and physics. The context within a broader collection of similar simulations further enhances its educational value.

Lissajous Curves Study Guide

Quiz

Who is credited with the study of Lissajous curves, and what were his years of life?
According to the text, what mathematical functions are Lissajous curves a composition of? Provide the general forms of the equations for x and y.
What is identified as the key factor that significantly influences the shape of a Lissajous curve?
What actions can a user take within the provided JavaScript simulation to observe different Lissajous figures?
The simulation includes three buttons labeled A, B, and C. What is the purpose of these buttons?
Who are listed as the authors of the JavaScript simulation applet described in the text?
The text mentions that the amplitude of the Lissajous curves in the simulation is set to a specific value. What is this value?
Besides frequency, what other parameter in the y-equation can be adjusted in the simulation to alter the Lissajous curve?
Where on the webpage can a user find the option to embed the Lissajous curve simulation into another webpage?
What are the stated disciplines or subject areas under which this Lissajous Curves simulation is categorized on the website?

Quiz Answer Key

Jules Antoine Lissajous, a French physicist and mathematician, is credited with the study of Lissajous curves. He lived from 1822 to 1880.
Lissajous curves are the composition of two harmonic motions, also known as sinusoids. The general forms are: x = amplitude * cos (frequency1 * time) and y = amplitude * cos (frequency2 * time + phase).
The shape of Lissajous curves is highly sensitive to the ratio of the two frequencies, frequency1/frequency2.
Users can experiment with different numerical values for the frequencies and the phase using the fields provided in the simulation. They can also click the predefined buttons A, B, and C.
The three buttons (A, B, and C) are designed to set predefined values for the frequency and the phase of the harmonic signals, allowing users to quickly observe different Lissajous figures.
The authors of the JavaScript simulation applet are Alfonso Urquía and Carla Martín from the Dpto. de Informática y Automática, E.T.S. Ingeniería Informática, UNED in Madrid, Spain.
The amplitude of the Lissajous curves in this simulation is set to 30.
Besides frequency (frecuency2), the phase in the y-equation can be adjusted in the simulation to alter the Lissajous curve.
The "Embed" option, along with an iframe code snippet, is located directly below the "Lissajous Curves JavaScript Simulation Applet HTML5" heading and the breadcrumbs.
The Lissajous Curves simulation is categorized under Mathematics (specifically Functions and graphs) and Physics (specifically under Newtonian Mechanics and Pressure in the breadcrumbs).

Essay Format Questions

Discuss the mathematical principles behind the formation of Lissajous curves. Explain how the interplay between amplitude, frequency ratio, and phase difference in the two harmonic motions determines the resulting shapes.
Explain how the provided JavaScript simulation can be used as a tool for learning about Lissajous curves. Describe the interactive features and how they allow users to explore the relationship between the input parameters and the visual output.
Based on the information given, discuss the significance of the frequency ratio (frequency1/frequency2) in determining the appearance of Lissajous figures. How does changing this ratio affect the complexity and periodicity of the curves?
Considering the authors and their affiliation, speculate on the intended audience and educational context for this Lissajous curve simulation. What aspects of the simulation design might be particularly beneficial for this audience?
Beyond the specific example of Lissajous curves, discuss the broader concept of combining harmonic motions in physics and mathematics. What are some other phenomena or applications where the superposition of sinusoidal functions is important?

Glossary of Key Terms

Lissajous Curves: Parametric curves formed by the combination of two sinusoidal functions with perpendicular axes. Their shape is determined by the frequency ratio, amplitudes, and phase difference of the two sinusoids.
Harmonic Motion (Sinusoid): A periodic oscillation that can be described by a sine or cosine function. It is characterized by its amplitude, frequency, and phase.
Amplitude: The maximum displacement or height of a wave or oscillation from its equilibrium position. In the context of Lissajous curves, it scales the size of the oscillation along the x and y axes.
Frequency: The number of complete cycles of an oscillation that occur in a unit of time, usually measured in Hertz (Hz). In Lissajous curves, the ratio of the two frequencies is crucial for determining the shape.
Phase: The initial angle of a sinusoidal function at its starting point (time = 0). In Lissajous curves, the phase difference between the two sinusoidal components affects the orientation and starting point of the resulting curve.
Parametric Curve: A curve whose coordinates (x, y) are both expressed as functions of an independent variable, often time (t) in physics contexts. Lissajous curves are a type of parametric curve.
Frequency Ratio: The ratio between the frequencies of the two sinusoidal functions that combine to form a Lissajous curve (frequency1/frequency2). This ratio is the primary determinant of the curve's shape.
Virtual-Lab: An online interactive simulation designed to mimic the experience of a physical laboratory experiment, allowing users to manipulate variables and observe the outcomes.
JavaScript Simulation Applet: A small, interactive program written in the JavaScript programming language that runs within a web browser, allowing users to visualize and experiment with a specific concept (in this case, Lissajous curves).

Sample Learning Goals

[text]

For Teachers

Lissajous curves are a family of parametric curves studied by the French physicist and mathematician Jules Antoine Lissajous (1822 - 1880).

Lissajous curves are the composition of two harmonic motions (sinusoids):
x = amplitude * cos ( frequency1 * time )
y = amplitude * cos ( frecuency2 * time + phase )

The shape of the curves is highly sensitive to the ratio frequency1/frequency2.
There are 3 curves A, B, and C in this simulation, which is vastly different from each other. The amplitude of the curve is set to 30, but both frequencies and the phase can be changed.

Do experiment with different values of the frequencies and the phase using the fields provided in the simulation, and see how the graph changes.

Research

[text]

Video

[text]

Version:

Other Resources

[text]

Frequently Asked Questions about the Lissajous Curves Simulation

1. What are Lissajous curves?

Lissajous curves are graphical representations formed by combining two independent sinusoidal motions along perpendicular axes (typically x and y). They are parametric curves where the x and y coordinates are defined as sinusoidal functions of time.

2. Who discovered and studied Lissajous curves?

Lissajous curves were studied by the French physicist and mathematician Jules Antoine Lissajous (1822 - 1880).

3. How are Lissajous curves mathematically defined in this simulation?

In this simulation, the Lissajous curves are defined by the following parametric equations: x = amplitude * cos ( frequency1 * time ) y = amplitude * cos ( frequency2 * time + phase )

4. What factors significantly influence the shape of Lissajous curves?

The shape of Lissajous curves is highly sensitive to the ratio of the two frequencies (frequency1/frequency2) and the phase difference between the two sinusoidal motions.

5. How can I interact with the Lissajous curves simulation?

The simulation provides interactive fields where users can adjust the numerical values of the two frequencies and the phase. Additionally, there are three predefined settings (accessible via buttons A, B, and C) that demonstrate different Lissajous curves. Experimenting with these controls allows users to observe how changes in frequency and phase affect the resulting curve.

6. What is the purpose of the Lissajous curves virtual lab?

This virtual lab is designed to enable users to analyze Lissajous figures by manipulating the frequencies and phase of the harmonic signals that compose them and observing the resulting changes in the curve's shape.

7. What is the amplitude of the Lissajous curves in this specific simulation?

In this simulation, the amplitude of both the x and y components of the Lissajous curves is set to 30. However, the frequencies and the phase can be varied by the user.

8. Where can I find and embed this Lissajous curves simulation?

The simulation can be embedded into a webpage using the provided iframe code:

Additionally, alternative versions of this simulation can be found at the provided URLs.

1 1 1 1 1 1 1 1 1 1 Rating 0.00 (0 Votes)

Details: Written by Wei Chiong; Parent Category: Pure Mathematics; Category: 1 Functions and graphs; Published: 04 May 2018; Created: 04 May 2018; Last Updated: 22 March 2025; Hits: 7069