About

7.3.7 Gravitational Potential (symbol: ϕ and units: J kg^-1)

The gravitational potential, ϕ , at a point due to the gravitational field set up by a mass M is defined as the work done per unit mass in bringing a point mass from infinity to that point.

Mathematically, it can be shown that $\varphi =-\genfrac{}{}{0.1ex}{}{GM}{r}$

7.3.7.1 Equation U = mϕ

1) This expression $\varphi =-\genfrac{}{}{0.1ex}{}{GM}{r}$ is similar to the expression for gravitational potential energy, $U=-m\genfrac{}{}{0.1ex}{}{GM}{r}$. and they are related by U = mϕ.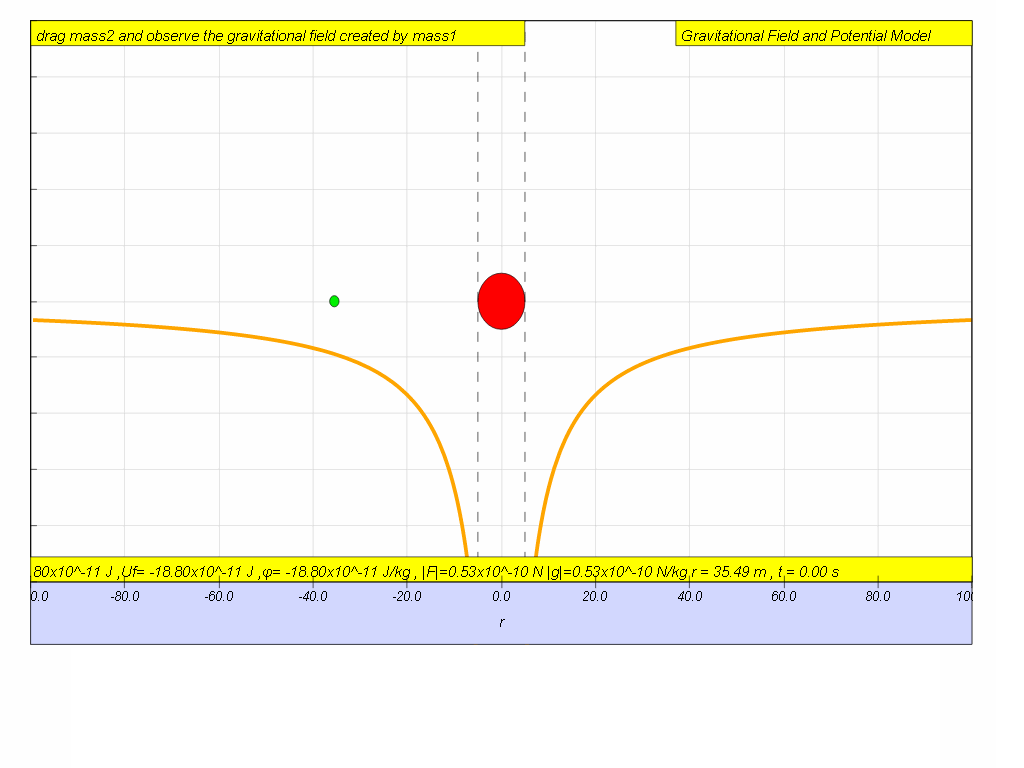

7.3.7.2 Scalar quantity

2)    Gravitational potential is a scalar quantity. (i.e. it has no direction and a negative value simply means it is less than zero).

7.3.7.3 Always negative

3)    This expression implies that ϕ is also always negative (less than zero) and by convention, the gravitational potential at infinity is also taken to be zero (maximum).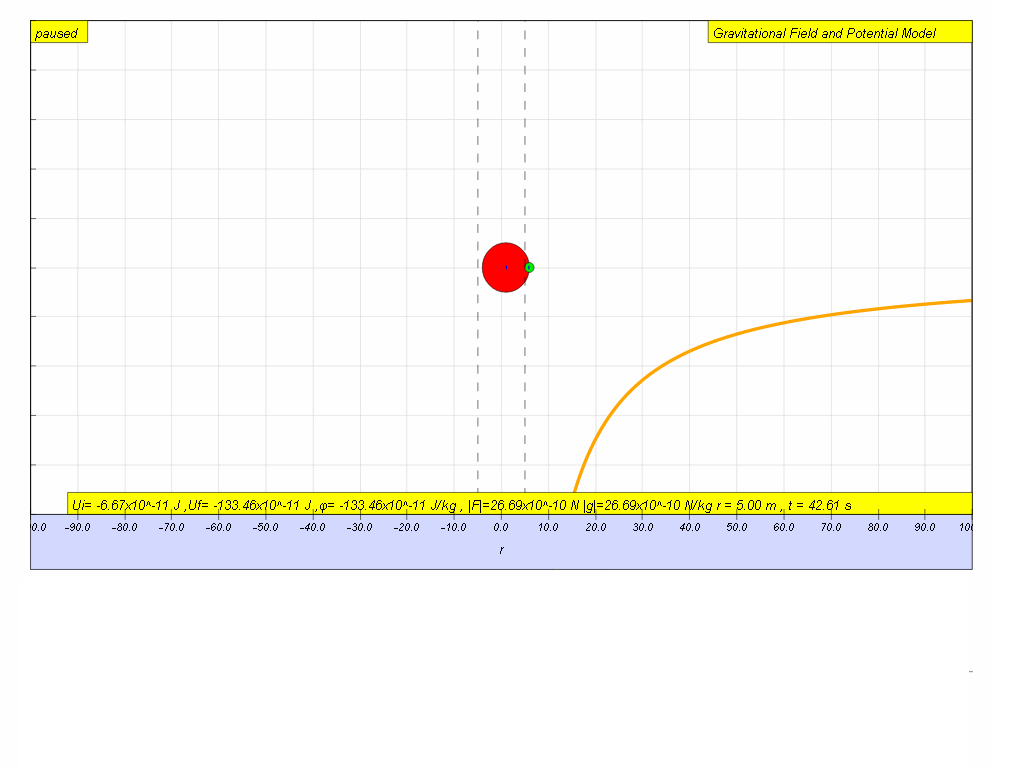

7.3.7.4 Independent of test mass

4)    Similar to gravitational field strength $g=\genfrac{}{}{0.1ex}{}{GM}{r^2}$, gravitational potential $\varphi =-\genfrac{}{}{0.1ex}{}{GM}{r}$ is also independent of the mass of the point mass, m. 

7.3.7.5 Vary according to inverse law with distance r

5)    As distance r of the point mass from source mass increases, ϕ increases according to the equation 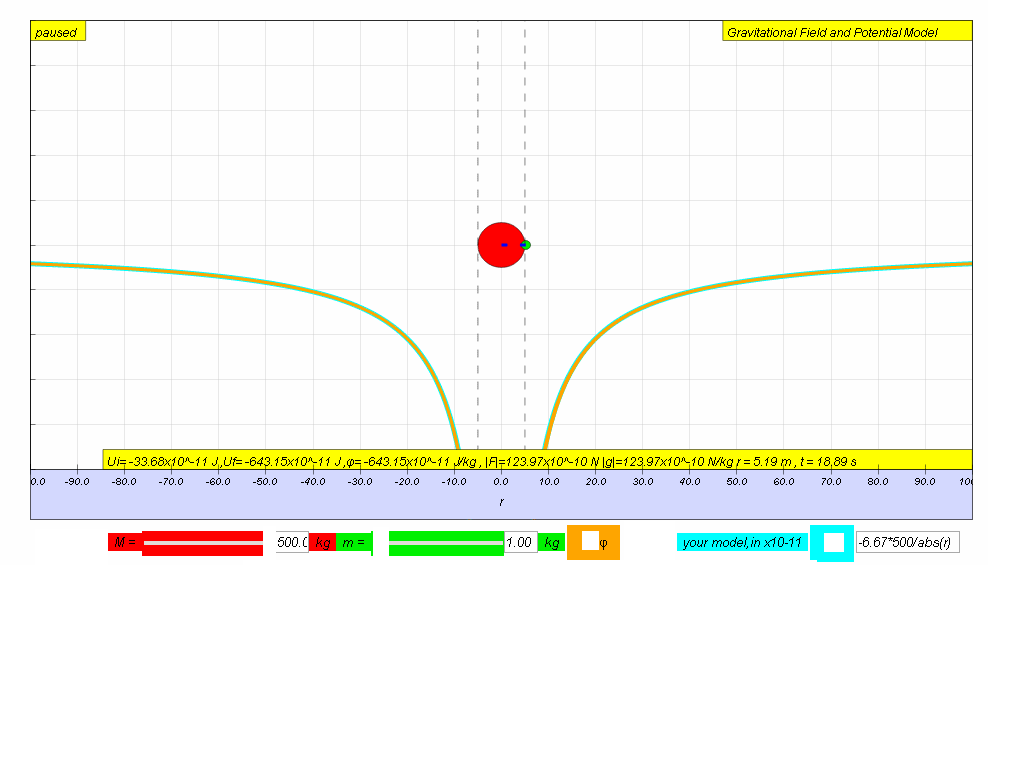$\varphi =-\genfrac{}{}{0.1ex}{}{GM}{r}$ .

7.3.8 Activity to do

ICT inquiry worksheet 1 (C) and (D), as well as the "G field and potential" EJS here. The HTML5 version is below, the Java worksheet customization to HTML5 is work in progress.

7.3.9 Summary

symbol	g	ϕ
name	Field strength	Potential
units	N kg-1 or m s-2	J kg-1
meaning	Gravitational force per unit mass	Gravitational potential energy per unit mass
quantity	vector	scalar
equation	$\mathrm{|g|}=\genfrac{}{}{0.1ex}{}{GM}{r^2}$ towards the centre of the source mass	$\varphi =-\genfrac{}{}{0.1ex}{}{GM}{r}$
relationship to mass	Force, $F=\frac{G{M}_1{M}_2}{r^2}$ = mg	Potential energy, $U=-m\genfrac{}{}{0.1ex}{}{GM}{r}$ = mϕ
graph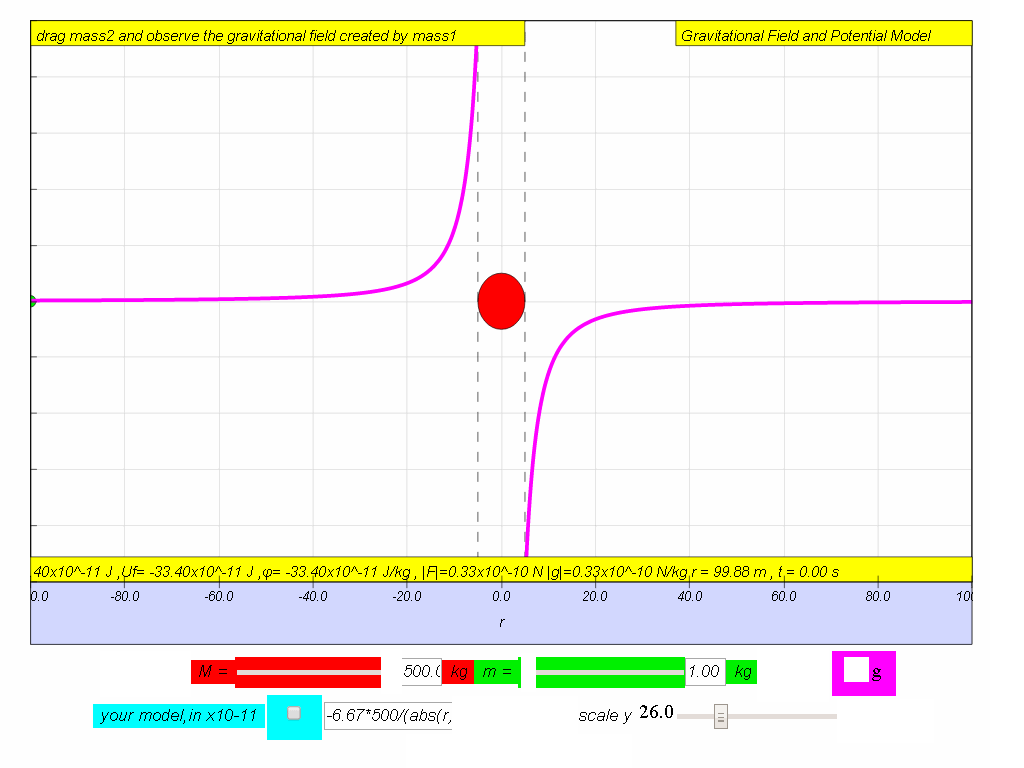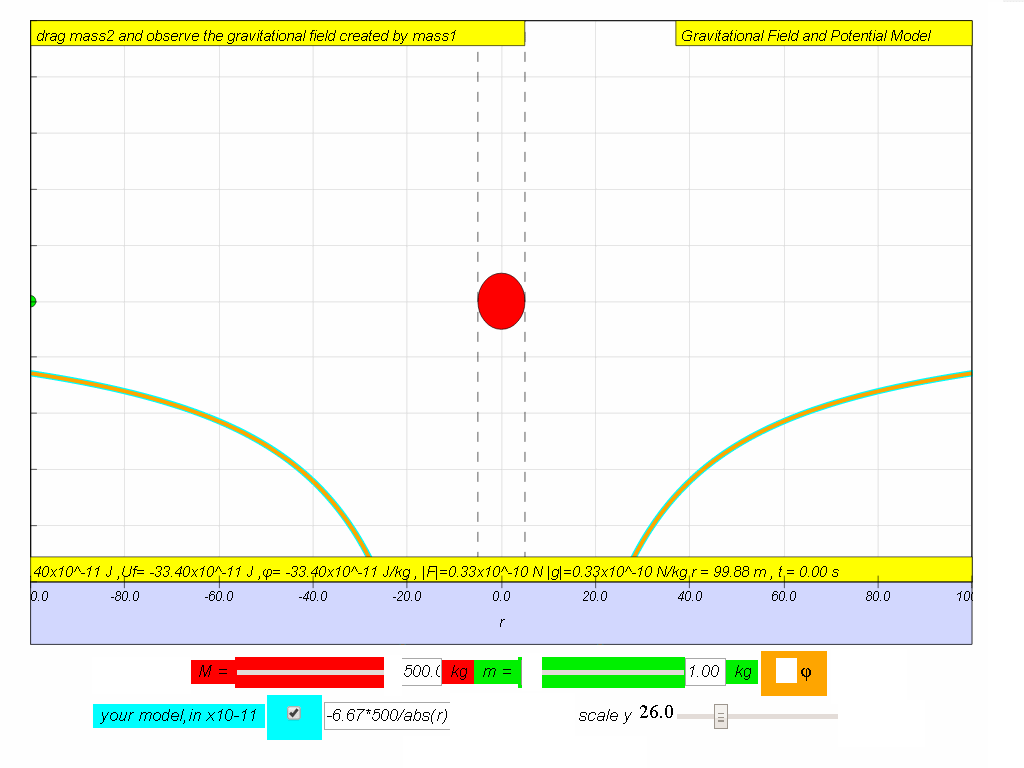
computer model if M = 500.	-6.67*500/(abs(r)*r)	-6.67*500/abs(r)

7.3.10 Modeling

Try to input your own model for potential until you achieve a close fit to the data set graph from potential.
Hint:
What is the value of M is the model?
no need to key in x10^-11
abs in JavaScript is absolute |   | that always make the value positive.
try something like -6.67*500/abs(r) in the equivalent for $\varphi =-\genfrac{}{}{0.1ex}{}{GM}{r}$

7.3.11 Model

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/58

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.; Anne Cox; Wolfgang Christian; Francisco Esquembre

http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejss_model_gravity06/gravity06_Simulation.xhtml

 

Resources

1. http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejs/ejs_model_GField_and_Potential_1D_v8wee.jar