About

http://weelookang.blogspot.sg/2010/11/ejs-open-source-lorentz-force-on.html

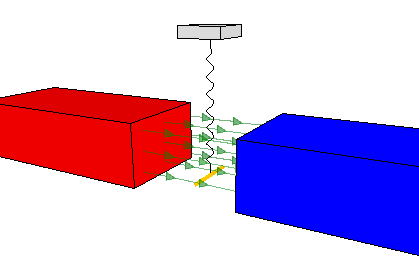
Lorentz force on a wire

This program simulates the force exerted by a magnetic field between two magnets on an electrical current trough a wire.

The wire is suspended on a spring and will oscillate when the battery (which is connected to the ends of the wire) is turned on and off, the angle of the wire with respect to the magnetic field is changed, or the poles of the magnets are switched.

new remixed version by lookang 20 Dec 2010

original version by Professor Francisco (Paco) Esquembre

Credits:

The Lorentz force on a wire model was created by Francisco (Paco) Esquembre, customized by Loo Kang Wee using the Easy Java Simulations (EJS) version 4.2 authoring and modeling tool.  An applet version of this model is available on the NTNU website < http://www.phy.ntnu.edu.tw/ntnujava/ >.

You can examine and modify this compiled EJS model if you run the model (double click on the model's jar file), right-click within a plot, and select "Open EJS Model" from the pop-up menu.  You must, of course, have EJS installed on your computer.  Information about EJS is available at: <http://www.um.es/fem/Ejs/> and in the OSP comPADRE collection <http://www.compadre.org/OSP/>.

Exercise by lookang 

Introduction www.bk.psu.edu/faculty/gamberg/mag_lab.doc
A current-carrying wire in a magnetic field experiences a force. The magnitude and direction of this force F, depend on four variables: 
the magnitude and direction of the current (I), 
the strength and direction of the magnetic field (B)
the length of the wire expose to magnetic field is (L)
the angle between the current I and field B is (ϑ) 
Advanced: The force can be described mathematically by the vector cross-product:
O level: Fleming’s Left Hand Rule predicts the using the left hand, F (thumb) B (index finger) I (middle finger) 
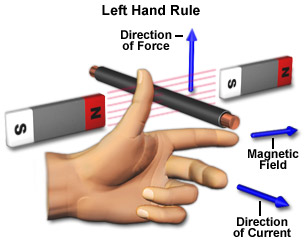
image from National High Magnetic Field Laboratoryhttp://www.magnet.fsu.edu/education/tutorials/java/handrules/index.html

Advanced: F = I ^ B. L where ^ is the cross product 
O level and A level: F = I . B. L.sin ϑ where ϑ is the angle between I and B 

where
Force F is in newtons N
current I is in amperes A
length L in meters m
magnetic field B in teslas T

The direction of the force F is perpendicular to both the current I and the magnetic field B, and is predicted by the Advanced: right-hand cross-product rule. 
O level and A level: Fleming’s Left Hand Rule

Engage:
a real live demo is the best.!!
a youtube video http://www.youtube.com/watch?v=_X8jKqZVwoI&feature=player_embedded
Engage 1: Would you believe that a wire can jump up even though it is not alive?
Engage 2: have you thought about how a direct current can cause a rotating motion which can be used to drive some simple toys (e.g Tamiya cars) ? 
http://www.tamiya.com/english/products/42183trf502x/top.jpg


Explore
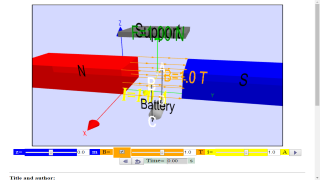
1. Explore the simulation, this simulation is designed with a wire supported by a spring in a system of magnetic fields in y direction.
2 The play button runs the simulation, click it again to pause and the reset button brings the simulation back to its original state.
3 by default values B, I, L, play the simulation. Notice that the wire is in its motionless in its previous state of motion. What is the physics principle simulatted here.
hint: newton's 1st law
4 reset the simulation.
5 using the default values(L = 1 m, ϑ = 90 deg), adjust the value of By =1 and Ix =1 play the simulation. what did you observe? explain the motion in terms of the influences of magnetic field (assume gravitational effect can be neglected, in this computer model gravity is not model)
6 explore the slider z. what do this slider control?
7 explore the slider vz. what does this slider control?
8 by leaving the cursor on the slider, tips will appear to give a description of the slider. you can try it the following sliders such as the drag coefficient b.
9 there are some value of time of simulation t and the checkbox graph for height vs time. 
10 vary the simulation and get a sense of what it does.

11 reset the simulation
Mechanics
12 using the default values (By =0, Ix=0) set z = -0.6, vz=0, b=0). Observe the motion of the wire in the absence of magnetic field. Predict what you will see. Describe the motion of the wire. Explain why this it is so?
hint: select the checkbox to view the scientific graph of height vs t.
13 using the default values (By =0, Ix=0) set z = -0.6, vz=0, b=1). Observe the motion of the wire in the absence of magnetic field. Predict what you will see. Describe the motion of the wire. Explain why this it is so?
hint: select the checkbox to view the scientific graph of height vs t.
14 using the default values (By =0, Ix=0) set z = -0.6, vz=1, b=0). Observe the motion of the wire in the absence of magnetic field. Predict what you will see. Describe the motion of the wire. Explain why this it is so?
hint: select the checkbox to view the scientific graph of height vs t.
15 using the default values (By =0, Ix=0) set z = -0.6, vz=1, b=1). Observe the motion of the wire in the absence of magnetic field. Predict what you will see. Describe the motion of the wire. Explain why this it is so?
hint: select the checkbox to view the scientific graph of height vs t.
16 conduct more scientific inquiry into the simulation if need before the next part of the question.
Elaborate 
17 explain the effects of b, the model used is drag force = b.v.

18 reset the simulation
Magnetic Force
Evaluate:
19 A scientist hypothesis "O level and A level: F = I . B. L. where ϑ =90 deg" play the simulation for different initial condition and design an experiment with tables of values to record systematically, determine whether the hypothesis is accurate. 

20 what is the impact of the ϑ != 90 deg ?
21 Suggest a better hypothesis
22 This computer model does not build in gravity, suggest with reason(s) why you agree or disagree with this statement. You can examine and modify this compiled EJS model if you run the model (double click on the model's jar file), right-click within a plot, and select "Open EJS Model" from the pop-up menu.  You must, of course, have EJS installed on your computer.  Information about EJS is available at: and in the OSP comPADRE collection 


Have Fun!  

Translations

Code	Language		Translator	Run

Credits

Francisco (Paco) Esquembre; lookang (This email address is being protected from spambots. You need JavaScript enabled to view it.)

 

Sample Learning Goals

O level: Fleming’s Left Hand Rule predicts the using the left hand, F (thumb) B (index finger) I (middle finger)

A level

A current-carrying wire in a magnetic field experiences a force. The magnitude and direction of this force F, depend on four variables:
the magnitude and direction of the current (I),
the strength and direction of the magnetic field (B)
the length of the wire expose to magnetic field is (L)
the angle between the current I and field B is (ϑ)
Advanced: The force can be described mathematically by the vector cross-product:

For Teachers

This program simulates the force exerted by a magnetic field between two magnets on an electrical current trough a wire.
The wire is kept in equilibrium in the absence of gravity, suspended on a spring and will oscillate when the battery (which is connected to the ends of the wire) is turned on and off, the angle of the wire with respect to the magnetic field is changed, or the poles of the magnets are switched.
reference:http://www.walter-fendt.de/ph14e/lorentzforce.htm

Introduction

A current-carrying wire in a magnetic field experiences a force. The magnitude and direction of this force F, depend on four variables:
the magnitude and direction of the current (I),
the strength and direction of the magnetic field (B)
the length of the wire expose to magnetic field is (L)
the angle between the current I and field B is (ϑ)
Advanced: The force can be described mathematically by the vector cross-product:
O level: Fleming’s Left Hand Rule predicts the using the left hand, F (thumb) B (index finger) I (middle finger)
image from National High Magnetic Field Laboratory http://www.magnet.fsu.edu/education/tutorials/java/handrules/index.html

Advanced: F = I ^ B. L where ^ is the cross product
O level and A level: F = I . B. L.sin ϑ where ϑ is the angle between I and B

where
Force F is in newtons N
current I is in amperes A
length L in meters m
magnetic field B in teslas T

The direction of the force F is perpendicular to both the current I and the magnetic field B, and is predicted by the Advanced: right-hand cross-product rule.
O level and A level: Fleming’s Left Hand Rule

Engage

Engage:
a real live demo is the best.!!
A youtube video http://www.youtube.com/watch?v=_X8jKqZVwoI&feature=player_embedded



Engage 1: Would you believe that a wire can jump up even though it is not alive?
Engage 2: have you thought about how a direct current can cause a rotating motion which can be used to drive some simple toys (e.g Tamiya cars) ?
http://www.tamiya.com/english/products/42183trf502x/top.jpg

 

Explore

1. Explore the simulation, this simulation is designed with a wire supported by a spring in a system of magnetic fields in y direction.
2 The play button runs the simulation, click it again to pause and the reset button brings the simulation back to its original state.
3 by default values B, I, L, play the simulation. Notice that the wire is in its motionless in its previous state of motion. What is the physics principle simulatted here.
hint: newton's 1st law
4 reset the simulation.
5 using the default values(L = 1 m, ϑ = 90 deg), adjust the value of By =1 and Ix =1 play the simulation. what did you observe? explain the motion in terms of the influences of magnetic field (assume gravitational effect can be neglected, in this computer model gravity is not model)
6 explore the slider z. what do this slider control?
7 explore the slider vz. what does this slider control?
8 by leaving the cursor on the slider, tips will appear to give a description of the slider. you can try it the following sliders such as the drag coefficient b.
9 there are some value of time of simulation t and the checkbox graph for height vs time.
10 vary the simulation and get a sense of what it does.

11 reset the simulation
Mechanics
12 using the default values (By =0, Ix=0) set z = -0.6, vz=0, b=0). Observe the motion of the wire in the absence of magnetic field. Predict what you will see. Describe the motion of the wire. Explain why this it is so?
hint: select the checkbox to view the scientific graph of height vs t.
13 using the default values (By =0, Ix=0) set z = -0.6, vz=0, b=1). Observe the motion of the wire in the absence of magnetic field. Predict what you will see. Describe the motion of the wire. Explain why this it is so?
hint: select the checkbox to view the scientific graph of height vs t.
14 using the default values (By =0, Ix=0) set z = -0.6, vz=1, b=0). Observe the motion of the wire in the absence of magnetic field. Predict what you will see. Describe the motion of the wire. Explain why this it is so?
hint: select the checkbox to view the scientific graph of height vs t.
15 using the default values (By =0, Ix=0) set z = -0.6, vz=1, b=1). Observe the motion of the wire in the absence of magnetic field. Predict what you will see. Describe the motion of the wire. Explain why this it is so?
hint: select the checkbox to view the scientific graph of height vs t.
16 conduct more scientific inquiry into the simulation if need before the next part of the question.
Elaborate
17 explain the effects of b, the model used is drag force = b.v.

18 reset the simulation
Magnetic Force
Evaluate:
19 A scientist hypothesis "O level and A level: F = I . B. L. where ϑ =90 deg" play the simulation for different initial condition and design an experiment with tables of values to record systematically, determine whether the hypothesis is accurate.

20 what is the impact of the ϑ != 90 deg ?
21 Suggest a better hypothesis
22 This computer model does not build in gravity, suggest with reason(s) why you agree or disagree with this statement. You can examine and modify this compiled EJS model if you run the model (double click on the model's jar file), right-click within a plot, and select "Open EJS Model" from the pop-up menu.  You must, of course, have EJS installed on your computer.  Information about EJS is available at: and in the OSP comPADRE collection


Have Fun!

 

Research

[text]

Video

Electromagnetism (part 1): Force acting on a current-carrying conductor in a magnetic field by ETDtogo https://www.youtube.com/watch?v=URgZQ76tV1Y 

 Version:

1. http://weelookang.blogspot.sg/2016/06/fleming-left-hand-rule-or-lorentz-force.html JavaScript version
   
2. http://weelookang.blogspot.sg/2010/11/ejs-open-source-lorentz-force-on.html
3. Ejs Open Source Lorentz force on a current carrying wire java applet NTNUJAVA Virtual Physics Laboratory Java version
4. http://www.compadre.org/osp/items/detail.cfm?ID=10543&S=7 Java version

Other Resources

1. http://www.walter-fendt.de/ph14e/lorentzforce.htm
   

end faq

{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}