About

Tracker Modeling in Uniform Circular Motion of Fan

For Teachers

- Rotating fan.mp4
- Worksheet-BT Workshop.doc

Credits

Author: lookang model, jitning video
Contact: This email address is being protected from spambots. You need JavaScript enabled to view it.

Document Brief: Uniform Circular Motion Analysis Using Tracker Software

This document provides an overview of the physics principles and methodologies applied to analyze the uniform circular motion of a fan blade using Tracker, a free video analysis and modeling tool. The experiment examines the relationship between angular displacement, velocity, and acceleration, visualizing these parameters in synchronized graphs and a recorded video.

Purpose:

To help students and educators understand uniform circular motion by interpreting tracked motion data and visual representations.

Key Features:

• Analysis of position vs. time and velocity vs. time graphs.
• Visualization of circular motion using plotted trajectories.
• Detailed measurements for angular velocity and linear displacement.
• Synchronized motion with corresponding graphical data.

Study Guide: Understanding Uniform Circular Motion Using Tracker

Learning Objectives:

1. Understand the concept of uniform circular motion and its defining parameters.
2. Analyze motion data to determine angular velocity, frequency, and period.
3. Learn how to interpret position and velocity graphs for circular motion.

Step-by-Step Guide:

1. Setup and Recording:

   • Use Tracker to import the video of a fan blade in motion.
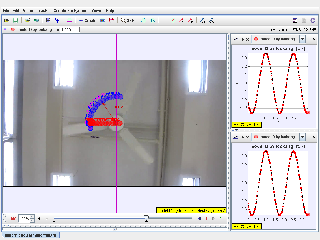
   • Establish a coordinate system for tracking the motion (as shown in the purple grid).

2. Tracking Motion:

   • Identify a fixed point on the fan blade and use the Tracker software to record its motion frame by frame.
   • Observe the blue trajectory and red plotted data in the interface.

3. Graph Analysis:

   • Examine the x-position vs. time graph to visualize sinusoidal motion due to projection.
   • Look at the y-position vs. time graph, which remains constant if motion is horizontal.
   • Identify the period (T) and amplitude of the sine wave to calculate angular velocity using ω=2πT\omega = \frac{2\pi}{T}ω=T2π​.

4. Applications:

   • Calculate linear velocity using $v=r\omega$, where $r$ is the radius of the circular path.
   • Compare experimental data with theoretical predictions.

Tips for Success:

• Ensure proper calibration of the Tracker coordinate system to maintain data accuracy.
• Cross-check measured data points with real-time video motion for validation.

FAQ: Uniform Circular Motion Analysis

1. What is uniform circular motion?

Uniform circular motion occurs when an object moves in a circle at a constant speed. The velocity changes direction continuously, creating centripetal acceleration.

2. Why does the x-position graph look sinusoidal?

The sinusoidal graph reflects the projection of circular motion onto the x-axis, illustrating harmonic motion over time.

3. How is angular velocity calculated?

Angular velocity ($\omega$) can be calculated using the equation ω=2πT\omega = \frac{2\pi}{T}ω=T2π​, where $T$ is the time period obtained from the graph.

4. Can I analyze vertical motion?

Yes. If the circular motion involves a vertical component, Tracker will show variations in the y-position graph as well.

5. What are the limitations of Tracker?

• Calibration errors can affect measurement accuracy.
• Limited frame rate of the video may lead to missing finer motion details.

6. How does this apply to real-world scenarios?

Uniform circular motion principles are foundational in understanding planetary orbits, mechanical rotors, and vehicle dynamics in curved paths.