About
**Unveiling the Mysteries of the Magic Square: Exploring the Enigma of 15**
In the realm of mathematics, there exists a captivating artifact known as the Magic Square. It's a puzzle that has mesmerized minds for centuries, offering a glimpse into the elegant symphony of numbers and patterns. Among its many enchanting qualities, one of the most intriguing is the property where the sums of the horizontal, vertical, and diagonal elements in a 3x3 square always add up to a constant value—15. Let's embark on a journey to unravel the secrets of this mystical arrangement.
### The Essence of Magic Square
Before delving into the depths of its magic, let's first understand what a Magic Square truly is. At its core, a Magic Square is a grid of numbers where the sum of each row, column, and diagonal is the same. The most basic form of this enigma is the 3x3 Magic Square, which consists of nine cells arranged in three rows and three columns.
### Exploring the 3x3 Magic Square
In the 3x3 Magic Square, each cell is filled with a unique integer from 1 to 9. The challenge lies in arranging these numbers in such a way that all rows, columns, and diagonals add up to the same constant value. And this is where the intrigue deepens—regardless of how you arrange the numbers within the square, the sum of the horizontal, vertical, and diagonal elements will always be 15.
### Unveiling the Mystery
Let's take a closer look at why the sum always equals 15. Consider the following arrangement:
```
8 1 6
3 5 7
4 9 2
```
If we sum the numbers in each row, column, and diagonal, we get:
- Horizontal sums: 8+1+6=15, 3+5+7=15, 4+9+2=15
- Vertical sums: 8+3+4=15, 1+5+9=15, 6+7+2=15
- Diagonal sums: 8+5+2=15, 6+5+4=15
No matter how we shuffle the numbers, the sum remains constant at 15, imbuing the square with its magical essence.
### The Mystique of Symmetry
One of the most captivating aspects of the Magic Square is its symmetry. Each row, column, and diagonal mirrors the others, creating a harmonious balance within the square. This symmetry is not only aesthetically pleasing but also serves as a testament to the elegance of mathematical patterns.
### Beyond the 3x3
While the 3x3 Magic Square is the most well-known, Magic Squares can take many forms and dimensions. From 4x4 to 5x5 and beyond, these squares continue to fascinate mathematicians and enthusiasts alike with their myriad possibilities and properties.
### Conclusion
In the realm of mathematics, the Magic Square stands as a testament to the beauty and complexity of numerical patterns. Within its seemingly simple arrangement lies a wealth of mysteries waiting to be explored. And as we uncover its secrets, we gain a deeper appreciation for the enchanting world of numbers and the wonders they hold.
So, the next time you encounter a 3x3 Magic Square, remember the magic of 15—the constant sum that binds its elements together in perfect harmony, leaving us in awe of its mystical allure.
To add on:
-
snapping feature should be deactivated when certain slot is occupied -
diagonals -
Color & visual markings to reach totalSum of 15
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.; coco
Sample Learning Goals
[text]
For Teachers
Technology as Replace Learning
In the realm of the magic square, the concept of replacement involves substituting elements while maintaining the fundamental properties of the square. The core essence of the magic square lies in the constant sum of the numbers along each row, column, and diagonal. Therefore, replacing one number with another within the square necessitates careful consideration to preserve this essential property.
For instance, in a 3x3 magic square where the numbers 1 through 9 are arranged such that each row, column, and diagonal sums up to 15, replacing any number with another would require ensuring that the new configuration still adheres to this rule. Thus, the challenge lies in finding alternative arrangements that maintain the integrity of the magic square while introducing variations in the numerical composition.
Technology as Amplify Learning
Amplification in the context of the magic square involves enhancing its properties or augmenting its capabilities while retaining its fundamental structure. we added automate addtional of the 3x3 elements in all directions to support patterns recognition.
Technology as Transform Learning
Transformation could be in the case of getting users to edit the source code of the interactive and getting them to make changes or redefine the traditional notion of the magic square.
Introducing Magic Square - Playing with Numbers
Introducing:
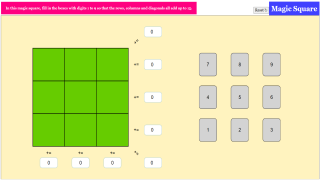
"Magic Square" is a captivating math simulation that revolves around the concept of arranging numbers in a 3 by 3 grid to create rows, columns, and diagonals that all add up to the same sum. In this case, the magic number is 15! The objective is simple: drag and move the card digits 1 to 9 into the green boxes within the square, ensuring that each row, column, and diagonal adds up to 15.
 |
| Link to Simulation Link to Joomla |
Upon launching the simulation, users are presented with a blank 3 by 3 grid and a set of card digits ranging from 1 to 9. By clicking and dragging the card digits into the green boxes, users must strategically place each number to achieve the magic sum of 15 in every row, column, and diagonal. As they arrange the numbers, the simulation provides instant feedback, highlighting any incorrect placements and guiding users towards the correct solution.
 |
| Link to Simulation Link to Joomla |
Why "Magic Square"?
"Magic Square" offers an array of benefits for users of all ages. Not only does it reinforce fundamental math concepts such as addition and problem-solving, but it also fosters critical thinking, spatial reasoning, and perseverance. Whether you're a student looking to sharpen your math skills or an educator seeking interactive teaching tools, "Magic Square" is the perfect blend of entertainment and education.
 |
| Link to Simulation Link to Joomla |
By challenging users to think critically and strategically, this interactive activity not only reinforces essential math skills but also cultivates problem-solving abilities and fosters a deeper understanding of numerical relationships.
Research
[text]
Video
[text]
Version:
https://weelookang.blogspot.com/2024/04/introducing-magic-square-playing-with.html
Other Resources
https://www.geogebra.org/m/zs5ghhzw
end faq
{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}
- Details
- Written by Coco Lee
- Parent Category: Interactive Resources
- Category: Mathematics
- Hits: 11525