About
Topics
Determination of frequency and wavelength
Stationary waves
Description
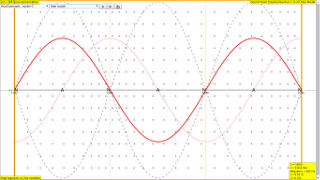
In this Open/Closed Pipe wave model, lets consider a narrow pipe along the OX axis. The simulation will display the first 5 normal modes, which are
From the drop-down menu, the mode n = 1, ...,5, may be selected.
Units are arbitrary set to be in SI unit for calculation purposes
The modeling equation is governed by u(t,x) where
- u(t,x) = A sin(n π x) cos(ω t + δ) when both ends are closed.
- u(t,x) = A sin((n-1/2) π x) cos(ω t + δ) when the left end is closed and the right end open.
- u(t,x) = A cos((n-1/2) π x) cos(ω t + δ) when the left end is open and the right end closed.
- u(t,x) = A cos(n π x) cos(ω t + δ) when both ends are open.
Play with the Model. Test what you've learned by exploring the amplitudes, wavelengths, periods, frequencies and wave velocities.
Sample Learning Goals
(a) show an understanding and use the terms displacement, amplitude, phase difference, period,frequency, wavelength and speed
(b) deduce, from the definitions of speed, frequency and wavelength, the equation v = fλ
(c) recall and use the equation v = fλ
(f) analyse and interpret graphical representations of
(i) determine the wavelength of sound using stationary waves.
(a) explain and use the principle of superposition in simple applications
(b) show an understanding of experiments which demonstrate stationary waves using microwaves, stretched strings and air columns
(c) explain the formation of a stationary wave using a graphical method, and identify nodes and antinodes
Activities
- Compute the position of the nodes(always zero displacement) for mode number n=1,2,3,4,5 cases for an open-open end system of the air in the pipe.
- Use the simulation to check your calculation.
- select the correct modeling equation for fixed end string n=1,2,3,4,5 respectively.
- how can you suggest is the parameter that describe these series of stationary waves.
Version:
- http://weelookang.blogspot.sg/2015/08/ejss-standing-wave-in-pipe-model.html
- http://weelookang.blogspot.sg/2015/07/ejss-standing-wave-in-pipe-model.html
- http://iwant2study.org/lookangejss/04waves_12generalwaves/ejs/ejs_model_pipewee02.jar
- http://iwant2study.org/lookangejss/04waves_12generalwaves/ejs/ejs_model_pipestringwee01.jar
-
http://weelookang.blogspot.sg/2015/08/ejss-standing-wave-in-pipe-model.html
Standing waves in a pipe
Let us consider a narrow pipe along the OX axis. Each end may be open or closed. The simulation will display the first 5 normal modes, which are- u(t,x) = A sin(n π x) cos(ω t + δ) when both ends are closed.
- u(t,x) = A sin((n-1/2) π x) cos(ω t + δ) when the left end is closed and the right end open.
- u(t,x) = A cos((n-1/2) π x) cos(ω t + δ) when the left end is open and the right end closed.
- u(t,x) = A cos(n π x) cos(ω t + δ) when both ends are open.
- Units are arbitrary.
- Below you may choose the mode n = 1, ...,5, as well as the animation step Δt.
- The upper animation shows the displacement field u(t,x) and the pressure p(t,x) as functions of x at each time t.
- In the lower animation you may see the evolution of the position x + u(t,x) of several points and a contour plot of p(t,x) (lighter/darker blue means higher/lower pressure).
- Optionally one can see the nodes where the displacement wave vanishes at all times.
- Scale has been arbitrarily enhanced to make things visible; but keep in mind that we are considering very small displacements and pressure changes in a narrow pipe.
- Put the mouse point over an element to get the corresponding tooltip.
Activities
- Compute the position of the nodes for mode number n in the four considered cases.
- Use the simulation to check your calculation.
- Where are the pressure nodes in the different cases?
- Which is the relationship between the displacement and pressure waves? How does it appears in the animation?
It requires Java 1.5 or newer and was created by Juan M. Aguirregabiria with Easy Java Simulations (Ejs) by Francisco Esquembre. I thank Wolfgang Christian and Francisco Esquembre for their help.
Translations
| Code | Language | Translator | Run | |
|---|---|---|---|---|
 |
||||
Credits


Juan M. Aguirregabiria (http://tp.lc.ehu.es/jma.html); lookang; tina
Briefing Document: 🔬Standing & Longitudinal Waves in a Pipe Simulation
1. Introduction
This document reviews the "Standing & Longitudinal waves in a pipe JavaScript HTML5 Applet Simulation Model" from Open Educational Resources / Open Source Physics @ Singapore. The simulation is an interactive tool designed to help students understand the behavior of standing waves within a pipe under various boundary conditions (open and closed ends). This briefing will outline the simulation's core features, the physics concepts it demonstrates, and its intended learning goals and activities.
2. Core Concepts & Simulation Description
- Standing Waves in Pipes: The simulation focuses on standing (or stationary) waves formed by the interference of incident and reflected waves within a pipe. It models longitudinal waves, where the displacement of particles is parallel to the wave's direction of travel.
- Normal Modes: The simulation displays the first 5 normal modes (n=1 to 5). Each mode represents a different pattern of oscillation, characterized by a specific number of nodes and antinodes.
- Boundary Conditions: The key focus of the simulation is on how the boundary conditions at the ends of the pipe affect the wave patterns. The simulation considers the following four cases, each with its own mathematical representation:
- Closed-Closed: Both ends of the pipe are closed. The displacement function is given by u(t,x) = A sin(n π x) cos(ω t + δ).
- Closed-Open: The left end is closed, and the right end is open. The displacement function is u(t,x) = A sin((n-1/2) π x) cos(ω t + δ).
- Open-Closed: The left end is open, and the right end is closed. The displacement function is u(t,x) = A cos((n-1/2) π x) cos(ω t + δ).
- Open-Open: Both ends of the pipe are open. The displacement function is u(t,x) = A cos(n π x) cos(ω t + δ).
- Displacement and Pressure: The simulation displays both the displacement of air particles (u(t,x)) and the corresponding pressure changes (p(t,x)) as functions of position (x) and time (t).
- The animation shows the displacement of air molecules.
- A contour plot visualizes the pressure variations: "lighter/darker blue means higher/lower pressure."
- Nodes and Antinodes: Users can observe the positions of nodes (points of zero displacement) in each mode. The simulation allows users to explore and compute the position of nodes, a key feature of standing waves. "Optionally one can see the nodes where the displacement wave vanishes at all times."
- Interactive Features: Users can:
- Choose the mode number n (1 to 5).
- Adjust the animation time step (Δt).
- Observe the displacement field and pressure changes over time.
- View the evolution of particle positions.
- Identify nodes in displacement waves.
- Tooltips provide additional information when hovering over the display.
3. Learning Goals
The simulation is designed to help students achieve the following learning goals:
- Understanding Wave Terminology: "show an understanding and use the terms displacement, amplitude, phase difference, period, frequency, wavelength and speed."
- Relationship between Speed, Frequency, and Wavelength: "deduce, from the definitions of speed, frequency and wavelength, the equation v = fλ" and "recall and use the equation v = fλ"
- Analyzing Wave Graphs: "analyse and interpret graphical representations of transverse and longitudinal waves"
- Determining Wavelength: "determine the wavelength of sound using stationary waves."
- Superposition Principle: "explain and use the principle of superposition in simple applications"
- Demonstrating Stationary Waves: "show an understanding of experiments which demonstrate stationary waves using microwaves, stretched strings and air columns."
- Formation of Stationary Waves: "explain the formation of a stationary wave using a graphical method, and identify nodes and antinodes."
4. Activities and Key Questions
The simulation provides several activities to guide student learning:
- Calculating Node Positions: Students are prompted to "Compute the position of the nodes(always zero displacement) for mode number n=1,2,3,4,5 cases for an open-open end system of the air in the pipe" and "Compute the position of the nodes for mode number n in the four considered cases." This reinforces the relationship between boundary conditions and wave patterns.
- Simulation Verification: Students are asked to "Use the simulation to check your calculation."
- Model Selection: Students must “select the correct modeling equation for fixed end string n=1,2,3,4,5 respectively."
- Parameter Identification: Students are challenged to think "how can you suggest is the parameter that describe these series of stationary waves."
- Pressure Node Locations: Students are asked, "Where are the pressure nodes in the different cases?"
- Relationship between Displacement and Pressure: Students are to explore "Which is the relationship between the displacement and pressure waves? How does it appears in the animation?"
The "Challenging Questions" section also highlights the relationship between compression/expansion and pressure/density, stating, "During compression, the molecules of the medium are forced together, resulting in the increased pressure and density. During expansion the molecules are forced apart, resulting in the decreased pressure and density. This coincide with the points of permanent zero amplitudes which are also called nodes."
5. Additional Resources & Context
- The provided URLs link to multiple related resources, including simulations of longitudinal waves, standing waves, reflections, and the speed of sound.
- The simulation is a translation of an original Basque resource, developed using Easy Java Simulations (Ejs).
- The page also lists other simulations related to oscillations and waves, suggesting the user has access to further learning materials
- It is explicitly mentioned that "Scale has been arbitrarily enhanced to make things visible; but keep in mind that we are considering very small displacements and pressure changes in a narrow pipe."
6. Conclusion
The "Standing & Longitudinal waves in a pipe JavaScript HTML5 Applet Simulation Model" is a valuable interactive learning resource. It enables students to explore the complex behavior of standing waves in pipes, visualize the relationships between displacement and pressure, and solidify their understanding of key wave concepts. The hands-on activities and challenging questions promote a deeper engagement with the material. The simulation's adjustable parameters make it suitable for diverse learning styles and levels. By using this tool, students can transition from theoretical understanding to an intuitive grasp of how boundary conditions dictate the standing wave patterns in a pipe.
Standing Waves in a Pipe Study Guide
Quiz
Answer the following questions in 2-3 sentences each:
- What are the four different end conditions for a pipe that the simulation models, and how does each impact the wave equation?
- In the context of standing waves, what is a node, and what are its characteristics regarding displacement and pressure?
- How does the simulation help illustrate the relationship between displacement and pressure waves in a pipe?
- What is the principle of superposition, and how does it apply to the formation of standing waves?
- What is the purpose of the "mode number" (n) in the wave equations, and how does changing the value of n affect the standing wave pattern?
- What is the relationship between wavelength, frequency, and wave speed, and what equation expresses this relationship?
- How does the simulation demonstrate the arbitrary nature of the units used for calculations?
- Explain the difference between transverse and longitudinal waves, focusing on the direction of particle motion relative to wave propagation.
- What practical experiments are mentioned that demonstrate stationary waves, and what mediums do they use?
- How do the graphical representations in the simulation help you understand the concept of standing waves?
Quiz Answer Key
- The simulation models pipes with four different end conditions: both ends closed, left end closed and right end open, left end open and right end closed, and both ends open. Each end condition affects the spatial part of the wave equation, using sine or cosine functions with either n or n-1/2 multiples of πx.
- A node is a point along a standing wave where the displacement is always zero. At nodes, the pressure variations are at a maximum due to the compression and expansion of the medium.
- The simulation shows how the displacement and pressure waves are related, with the nodes of the displacement wave being areas of maximum pressure variation. This is visible through the animation of the displacement field u(t,x) and the pressure p(t,x).
- The principle of superposition states that when two or more waves overlap, the resulting displacement at any point is the sum of the displacements of the individual waves. This principle allows for the formation of standing waves where incident and reflected waves interfere.
- The mode number n determines the number of half-wavelengths that fit into the length of the pipe, thus dictating the specific standing wave pattern. As n increases, the number of nodes and antinodes increases, leading to higher frequency standing waves.
- The relationship between wavelength, frequency, and wave speed is expressed by the equation v = fλ, where v is the wave speed, f is the frequency, and λ is the wavelength. These properties are all interrelated.
- The simulation uses arbitrary units set to SI for calculation purposes. By not specifying physical units, the model can be used to learn physics principles, not specific applications.
- Transverse waves have particle motion perpendicular to the direction of wave propagation, while longitudinal waves have particle motion parallel to the direction of wave propagation, as seen in the case of pressure waves in a pipe.
- The source material mentions experiments demonstrating stationary waves using microwaves, stretched strings, and air columns. These experiments help show how standing waves can be observed using various mediums.
- The simulation uses graphical representations of displacement, pressure, and contour plots to show the amplitude changes, nodes, and antinodes in the standing waves. These visuals allow the user to better grasp the phenomena.
Essay Questions
- Discuss the impact of different end conditions (open or closed) on the formation and characteristics of standing waves in a pipe. Consider the displacement, pressure, and frequencies possible in these varying conditions.
- Explain how the simulation’s visual representation and interactive capabilities enhance the understanding of standing wave phenomena and the relationships between parameters like mode number, frequency, wavelength, and speed.
- Analyze the relationship between the principle of superposition and the creation of standing waves in a pipe. Address how wave interference leads to nodes and antinodes and why these points are stationary.
- Describe how the simulation can be used to experimentally determine the wavelength of a sound wave. Explain how varying the mode number and observing the standing wave pattern reveals wave properties.
- Compare and contrast displacement and pressure waves within the context of standing waves in a pipe. Explore how they are related and how they are visualized by the simulation.
Glossary of Key Terms
Amplitude: The maximum displacement of a wave from its equilibrium position. Antinode: A point in a standing wave with maximum displacement and minimum pressure variation. Displacement: The distance and direction an individual particle in a medium has moved from its equilibrium position. Frequency: The number of wave cycles that pass a given point per unit of time, often measured in Hertz (Hz). Longitudinal Wave: A wave in which the particle motion is parallel to the direction of wave propagation, like pressure waves in a pipe. Mode Number (n): An integer that represents the specific pattern or harmonic of a standing wave. It determines the number of half-wavelengths that fit into the pipe. Node: A point in a standing wave where the displacement is always zero; pressure variation is a maximum here. Period: The time it takes for one complete wave cycle to occur, the reciprocal of frequency. Phase Difference: The difference in phase between two or more waves, describing their relative positions within a cycle. Pressure Wave: A longitudinal wave where changes in pressure propagate through a medium. Standing Wave (Stationary Wave): A wave pattern formed by the interference of two waves of the same frequency traveling in opposite directions, characterized by fixed nodes and antinodes. Superposition Principle: The principle that the net displacement at any point when two or more waves overlap is the sum of the individual wave displacements. Transverse Wave: A wave in which particle motion is perpendicular to the direction of wave propagation. Wavelength: The distance between two successive crests or troughs of a wave, or between two successive points in phase. Wave Speed: The speed at which a wave propagates through a medium, often represented as v.
Challenging Questions
Q1: Where does the greatest pressure occur?
A1: During compression, the molecules of the medium are forced together, resulting in the increased pressure and density. During expansion the molecules are forced apart, resulting in the decreased pressure and density. This coincide with the points of permanent zero amplitudes which are also called nodes. Refer to the simulations as N, nodes.
Other Resources
- http://physics.bu.edu/~duffy/HTML5/longitudinalwave.html
- http://physics.bu.edu/~duffy/HTML5/longitudinal_standing_wave.html
- http://physics.bu.edu/~duffy/HTML5/reflections.html
- http://physics.bu.edu/~duffy/HTML5/speed_of_sound.html
- http://weelookang.blogspot.sg/2015/08/ejss-standing-wave-in-pipe-model.html
- http://weelookang.blogspot.sg/2015/07/ejss-standing-wave-in-pipe-model.html
- http://iwant2study.org/lookangejss/04waves_12generalwaves/ejs/ejs_model_pipewee02.jar
- http://iwant2study.org/lookangejss/04waves_12generalwaves/ejs/ejs_model_pipestringwee01.jar
Other Hands-on Kit
- https://itunes.apple.com/us/app/spectrumview/id472662922?mt=8 contributed by Dave
- https://play.google.com/store/apps/details?id=processing.test.soundanalyzer contributed by Leong Tze Kwang and worksheet Sound Wave Experiment.docx
Video
FAQ on Standing Waves in Pipes
1. What are standing waves, and how do they form in pipes?
Standing waves, also known as stationary waves, are formed when two waves of the same frequency, amplitude, and wavelength travel in opposite directions and interfere with each other. In a pipe, these waves are typically sound waves. Reflections at the ends of the pipe cause these oppositely traveling waves, and at certain frequencies, they interfere constructively at some points (antinodes) and destructively at others (nodes), creating the characteristic pattern of a standing wave. These waves do not propagate through the medium, as with traveling waves, instead they oscillate in place.
2. How do the boundary conditions of a pipe affect the formation of standing waves?
The boundary conditions, whether the ends of a pipe are open or closed, significantly impact the possible standing wave patterns. A closed end acts as a displacement node (zero displacement), where air molecules cannot move freely, while an open end is a displacement antinode (maximum displacement), where air molecules can move. Therefore, a pipe with two closed ends will behave differently from a pipe with one open end and one closed end, or a pipe with both ends open. The different boundary conditions lead to different mathematical equations describing displacement.
3. What are nodes and antinodes in a standing wave, and what do they represent?
Nodes are locations in a standing wave where the displacement of the medium (air molecules in a pipe) is always zero. They appear as points of no movement in the animation of a standing wave. Antinodes, on the other hand, are locations where the displacement of the medium is at its maximum. In a pipe, these represent regions of maximum air molecule movement and pressure fluctuation. Nodes are associated with high pressure fluctuations and antinodes with low pressure fluctuations.
4. How do the different end conditions (open/closed) of a pipe affect the mathematical description of the standing wave?
The mathematical equations that describe the displacement of a standing wave within a pipe depend on the end conditions:
- Both Ends Closed: u(t,x) = A sin(nπx) cos(ωt + δ). The wave function is a sine wave with displacement nodes at the ends of the pipe.
- Left End Closed, Right End Open: u(t,x) = A sin((n-1/2)πx) cos(ωt + δ). The wave function is a sine wave, however, there is an offset of 1/2pi in the wavelength so that there is a displacement node at one end and an antinode at the other.
- Left End Open, Right End Closed: u(t,x) = A cos((n-1/2)πx) cos(ωt + δ). The wave function is a cosine wave, however, there is an offset of 1/2pi in the wavelength so that there is a displacement antinode at one end and a node at the other.
- Both Ends Open: u(t,x) = A cos(nπx) cos(ωt + δ). The wave function is a cosine wave with displacement antinodes at the ends of the pipe.
In these equations, u(t,x) is the displacement at position x and time t, A is the amplitude, n is the mode number (1, 2, 3...), ω is the angular frequency, and δ is the phase constant.
5. What is meant by "mode number" (n) in the context of standing waves in a pipe?
The mode number, n, refers to the different patterns of standing waves that can form within a pipe. It corresponds to the number of half-wavelengths that fit within the pipe. n = 1 represents the fundamental mode, where there is one antinode, n = 2 represents the second harmonic, n = 3 represents the third harmonic, and so on. Each mode has its own specific frequency and wavelength. The greater the mode number, the higher the frequency of the sound.
6. How is pressure related to displacement in a standing wave within a pipe?
In a standing wave, the pressure and displacement waves are not in phase. Where displacement is maximal (antinodes) the pressure fluctuation is minimal, and where the displacement is minimal (nodes) the pressure fluctuation is maximal. Therefore, pressure nodes correspond to displacement antinodes, and pressure antinodes correspond to displacement nodes. When air is compressed, pressure is high and displacement is minimal (a node), and when air is expanded, pressure is low and displacement is maximal (an antinode).
7. How can simulations help in understanding standing waves?
Simulations provide a visual and interactive way to explore standing waves, allowing users to observe how the waves behave over time in pipes. With a simulation, it becomes easier to visualise the movement of molecules and the pressure changes. They allow students to visualize displacement, pressure changes, the formation of nodes and antinodes, and the impact of different boundary conditions (open and closed ends) and mode numbers. This dynamic approach is more effective than static diagrams. Furthermore, the simulation enables students to compute the node locations and use the simulation to verify these values.
8. What are some real-world applications or examples of standing waves in pipes?
Standing waves in pipes are crucial in many real-world applications, particularly in musical instruments. Wind instruments, such as flutes, clarinets, and pipe organs, rely on the precise control of standing waves within their pipes to produce specific tones and pitches. By changing the length of the air column (e.g., using valves), the frequency of the standing wave is altered, which changes the pitch of the instrument. Understanding and manipulating standing wave physics is essential for designing and constructing these instruments.
- Details
- Parent Category: 03 Waves
- Category: 01 General Waves
- Hits: 15981