About

Multiple Slit Diffraction

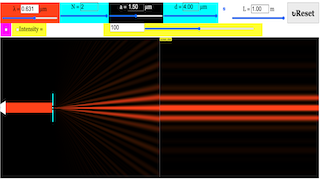
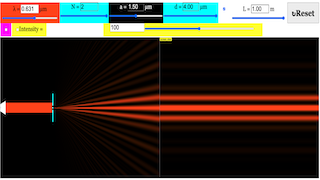
The EJS Multiple Slit Diffraction model allows the user to simulate Fraunhofer diffraction through single or multiple slits. The user can modify the number of slits, the slit width, the slit separation and the wavelength of the incident light. The scale of the diffraction pattern can also be changed and a plot of the light intensity can be toggled on and off with a checkbox.

 

The minima of single slit diffraction are determined by:

where D is the single slit width. For double slit interference, constructive interference (bright spots) are found at:

and destructive interference dark spots are located at:

where d is the distance between slits.

Multiple slits will sharpen (narrow) the regions of constructive interference.  The overall pattern from multiple slits will be the two-slit pattern multiplied by the single slit diffraction envelope.

References:

• Douglas Giancoli, Physics: Principles with Applications sixth edition, pages 664-675.
• Eugene Hecht, Optics fourth edition, pages 460-464.

Credits:

The Multiple Slit Diffraction model was created by Fu-Kwun Hwang using the Easy Java Simulations (EJS) modeling tool. It was adapted to EJS version 4.1 by Robert Mohr and Wolfgang Christian at Davidson College. You can examine and modify the model for this simulation if you have EJS installed by right-clicking within the diffraction frame and selecting "Open Ejs Model" from the pop-up menu. Information about EJS is available at: <http://www.um.es/fem/Ejs/> and in the OSP ComPADRE collection <http://www.compadre.org/OSP/>.

 

Translations

Code	Language		Translator	Run

Credits

Fu-Kwun Hwang,Robert Mohr, Wolfgang Christian; lookang; Félix J. García Clemente; Francisco Esquembre

http://iwant2study.org/lookangejss/04waves_11superposition/ejss_model_MultipleSlitDiffractionwee06/MultipleSlitDiffractionwee06_Simulation.xhtml

 

Sample Learning Goals

[text]

For Teachers

Young’s Slit Diffraction: Exploring Single, Double, and Multiple Slits with JavaScript HTML5 Applet

Diffraction and interference of light have fascinated physicists for centuries, ever since Thomas Young’s famous double-slit experiment demonstrated the wave nature of light. Today, you can experience the power of this phenomenon in a modern, interactive way through the Young’s Slit Diffraction Simulation Model, a versatile JavaScript-based HTML5 applet. This applet allows users to experiment with single, double, and even multiple slits, offering a deeper understanding of how light waves interfere and create diffraction patterns.

Explore the simulation here: Young’s Slit Diffraction Simulation Model

Single, Double, and Multiple Slit Diffraction Explained

• Single Slit Diffraction: In the case of a single slit, light passing through the slit diffracts, spreading out as it moves toward the observation screen. The resulting pattern shows a central bright fringe (the most intense) flanked by diminishing fringes on both sides.

• Double Slit Diffraction: In Young’s famous experiment, two slits create an interference pattern of alternating bright and dark fringes. The bright fringes appear where the light waves from the two slits constructively interfere (waves meet in phase), while dark fringes occur where the waves destructively interfere (waves meet out of phase).

• Multiple Slit Diffraction (Gratings): When more than two slits are used, the interference pattern becomes sharper and more defined. The central maximum remains prominent, but the side fringes become narrower and more distinct. As the number of slits increases, the intensity of these fringes also increases.

Interactive Power: Vary the Number of Slits

The Young’s Slit Diffraction Simulation Model now offers a powerful new feature: the ability to vary the number of slits. This functionality lets users go beyond just double-slit experiments, allowing them to simulate diffraction with any number of slits. By adjusting the number of slits (N) using a simple slider, users can visually see the profound impact this has on the diffraction pattern.

For example:

• N = 1 simulates a single-slit experiment, showing a wide central maximum with diminishing side fringes.
• N = 2 replicates Young’s classic double-slit interference pattern.
• N = 12 demonstrates a diffraction grating, where multiple slits produce sharp, well-defined maxima and minima.

This flexibility makes the applet a versatile educational tool for demonstrating how interference patterns evolve with changes in slit configuration.

Key Adjustable Parameters

This applet gives users control over several key parameters that affect the diffraction pattern:

• Wavelength (λ): Adjusting the wavelength of light shows how the spacing of the interference fringes changes with different colors of light.
• Slit Width (a): Changing the width of the slits allows users to explore how the diffraction envelope (the outer shape of the fringes) is modulated.
• Slit Separation (d): This affects the spacing of the interference fringes. Larger slit separations result in narrower spacing between the fringes, while smaller separations spread them out.
• Number of Slits (N): As discussed, this is the new, powerful feature that lets users experiment with multiple slits to visualize diffraction gratings.
• Screen Distance (L): This controls how far the observation screen is from the slits, affecting the spread of the interference pattern on the screen.

By combining these adjustable features, users can recreate experiments ranging from single-slit diffraction to highly complex diffraction gratings, all within a single simulation.

Educational Value and Real-Time Visualization

This HTML5 applet is an invaluable educational tool for teachers, students, and enthusiasts alike. With real-time visualization, students can instantly see how their adjustments impact the diffraction pattern. This hands-on approach enhances the learning experience, making abstract concepts more tangible and engaging.

The simulation offers a way to explore:

• Wave-particle duality of light: Demonstrating that light exhibits both wave-like and particle-like properties.
• Constructive and destructive interference: Visualizing how waves interact to form bright and dark fringes.
• Diffraction grating applications: Understanding how multiple slits can be used in practical applications like spectrometers.

How to Use the Applet for Classroom Demonstrations

Educators can use this applet to make lessons on wave optics and diffraction more interactive:

• Start with a single slit to show how light spreads out due to diffraction.
• Increase to two slits and discuss Young’s double-slit experiment and its historical significance in proving the wave nature of light.
• Gradually increase the number of slits to show how diffraction gratings work in real-world applications like spectroscopy.
• Adjust the wavelength slider to explore how different colors of light (from red to violet) affect the diffraction pattern, linking this to the electromagnetic spectrum.

By engaging students with these interactive features, you can foster a deeper understanding of wave optics and interference phenomena.

Conclusion

The Young’s Slit Diffraction Simulation Model brings the beauty of wave interference to life in an accessible, interactive way. With the added ability to vary the number of slits, users now have more control than ever to experiment with and visualize the fascinating patterns that emerge when light passes through slits.

Whether you're a physics teacher demonstrating diffraction to a class, a student preparing for an exam, or just curious about wave phenomena, this applet is a fantastic resource for exploring the principles of diffraction and interference.

Research

[text]

Video

[text]

 Version:

1. https://weelookang.blogspot.com/2021/08/young-double-slit-or-single-slit-or.html
2. https://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=2804.msg10149#msg10149 
3. https://www.compadre.org/osp/items/detail.cfm?ID=8331 
4. https://vle.learning.moe.edu.sg/moe-library/lesson/view/f7499ca4-6254-4429-83f5-fd1aafd35ea8/cover
5. https://weelookang.blogspot.com/2024/10/youngs-slit-diffraction-exploring.html

Other Resources

[text]

end faq

{accordionfaq faqid=accordion4 faqclass="lightnessfaq defaulticon headerbackground headerborder contentbackground contentborder round5"}