Breadcrumbs

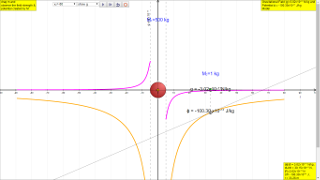
About

gravity07

7.3.8 Relationship between F and U; between g and ϕ

To understand how g is related to ϕ:

Similarly, compare $g = - \frac{G M}{r^{2}}$ and $ϕ = - \frac{GM}{r}$ in the above table.
If we differentiate $ϕ = - \frac{GM}{r}$ with respect to r, we will get $\frac{d ϕ}{d r} = - \frac{G M}{(- r^{2})}$ , which has the same expression as g.
Hence, mathematically $\frac{d ϕ}{d r} = \frac{G M}{r^{2}} = - g$
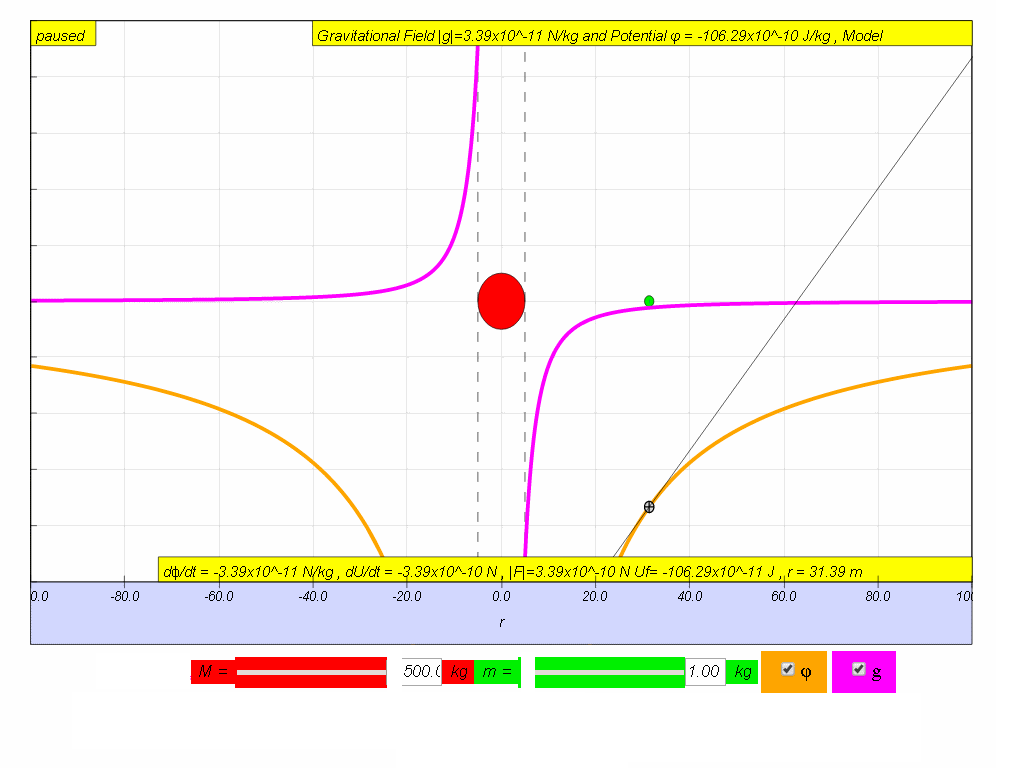
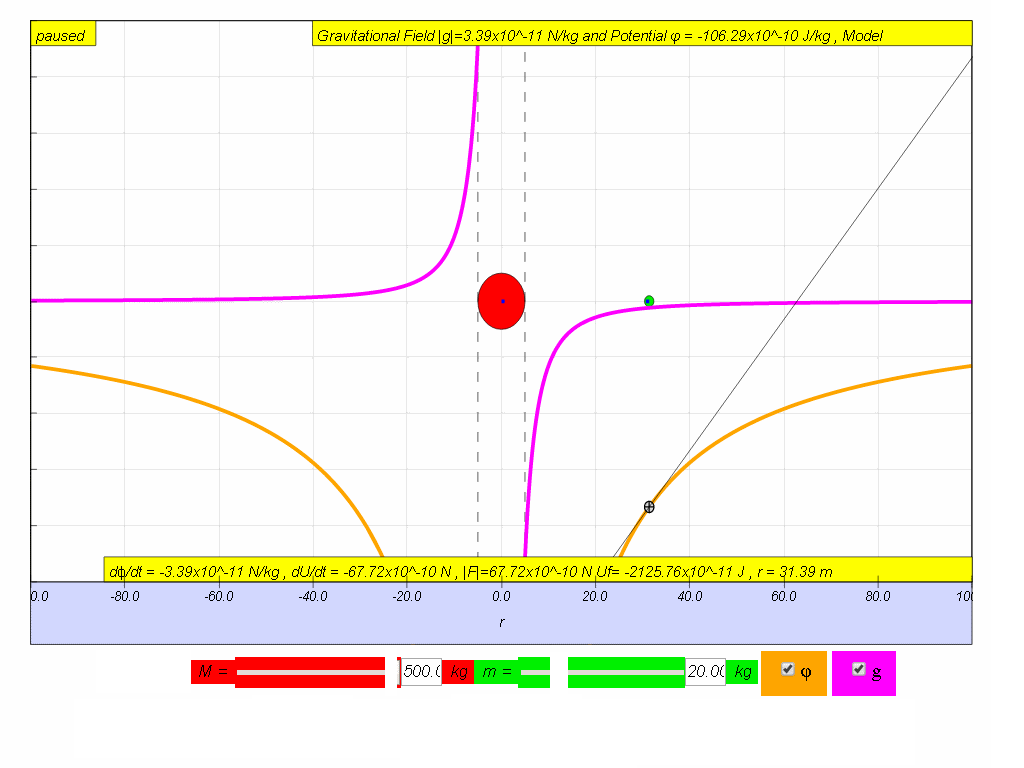
To understand the meaning of $g = - \frac{d ϕ}{d r}$ observe the two graphs carefully, on the right side where r is positive, the gradient of ϕ vs r graph is positive but the value of g will be negative. And on the left side where r is negative, the gradient of ϕ vs r graph is negative but the value of g is positive. Thus, $g = - \frac{d ϕ}{d r}$

Similarly, it can be concluded that by multiplying both sides by test mass m.

$m g = - \frac{d m ϕ}{d r}$
thus $F = - \frac{d m ϕ}{d r}$

7.3.8.1 Activity To do

ICT inquiry worksheet 1 (E), as well as the "G field and potential" EJS here. The HTML5 version is below, the Java worksheet customization to HTML5 is work in progress.

7.3.8.2 Summary

symbol	$g = - \frac{G M}{r^{2}}$	$ϕ = - \frac{GM}{r}$
name	Field strength	Potential
units	N kg^-1 or m s^-2	J kg^-1
meaning	Gravitational force per unit mass	Gravitational potential energy per unit mass
quantity	vector	scalar
equation	$\|g\| = \frac{G M}{r^{2}}$ towards the centre of the source mass	$ϕ = - \frac{GM}{r}$
relationship to mass	Force, $F = \frac{G M_{1} M_{2}}{r^{2}}$ = mg	Potential energy, $U = -m \frac{G M}{r}$ = mϕ
graph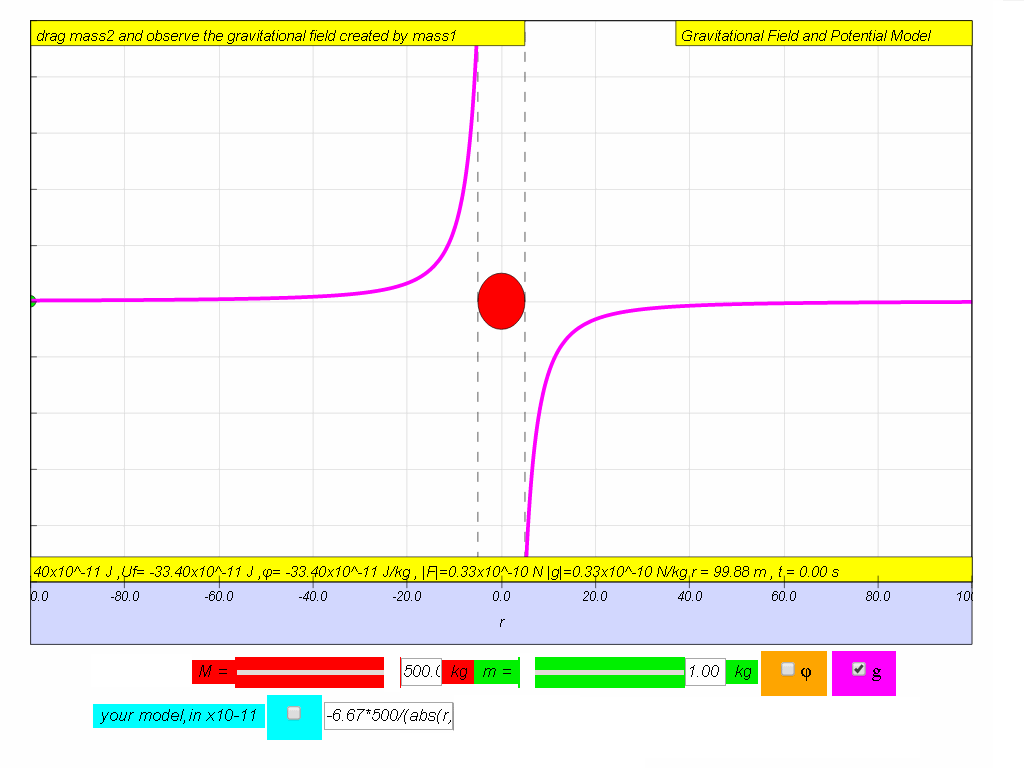
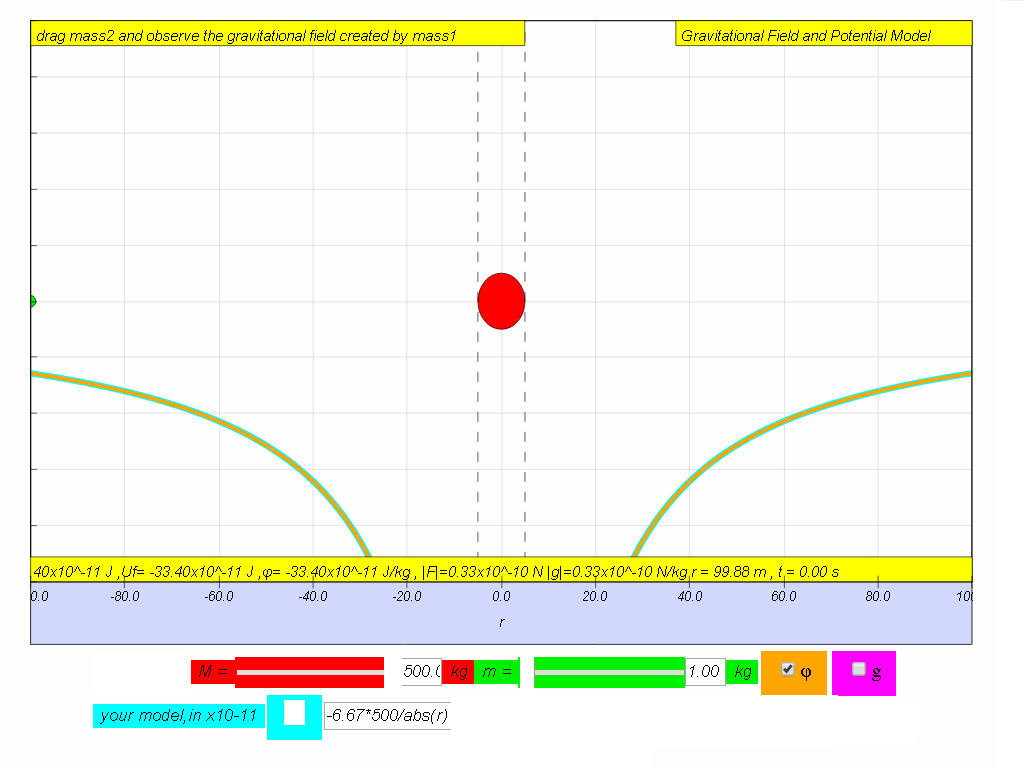computer model if M = 500.	-6.67500/(abs(r)r)	-6.67*500/abs(r)
relationship between g and ϕ	$g = - \frac{d ϕ}{d r}$
relationship between F and U	$F = - \frac{d U}{d r}$

7.3.8.3 Model

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.; Anne Cox; Wolfgang Christian; Francisco Esquembre

http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejss_model_gravity07/gravity07_Simulation.xhtml

Briefing Document: 🍎Relationship Between Gravitational Force, Potential, Field Strength, and Potential Energy

1. Introduction:

This document summarizes the key concepts and relationships presented in the Open Educational Resources / Open Source Physics @ Singapore resource, specifically section "7.3.8 Relationship between F and U; between g and φ". This section focuses on the mathematical and physical relationships between gravitational force (F), gravitational potential energy (U), gravitational field strength (g), and gravitational potential (φ). The resource uses a JavaScript HTML5 applet simulation model (gravity07) to help users visualize and understand these relationships.

2. Core Concepts & Relationships:

Gravitational Field Strength (g) and Gravitational Potential (φ):
Definitions: The resource defines g as "Gravitational force per unit mass" with units N/kg or m/s² and φ as "Gravitational potential energy per unit mass" with units J/kg.
Mathematical Relationship: The core idea is that g is the negative derivative of φ with respect to distance (r): "g = - dφ/dr".
Formulae:g = -GM/r²
φ = -GM/r
Where G is the gravitational constant, M is the mass of the source object, and r is the distance from the source.
Visualizing the Relationship: The resource states, "on the right side where r is positive, the gradient of ϕ vs r graph is positive but the value of g will be negative. And on the left side where r is negative, the gradient of ϕ vs r graph is negative but the value of g is positive. Thus, g = - dϕ/dr" This highlights that the field strength is related to the slope of the potential and the direction of the field is opposite to the direction of increasing potential.
Gravitational Force (F) and Gravitational Potential Energy (U):
Definitions: F is the force experienced by a mass due to gravity, and U is the potential energy a mass possesses due to its position in a gravitational field.
Mathematical Relationship: Similar to g and φ, the force F is the negative derivative of potential energy U with respect to distance (r): "F = - dU/dr". This relationship is derived by multiplying the equation for g by a test mass m: "m g = -d (m φ) / dr, thus F = -d (m φ) / dr".
Formulae:F = GM₁M₂/r² or F=mg
U= -mGM/r or U= mφ
Where M₁ and M₂ are the two masses involved in the gravitational interaction and m is the test mass.
Key Table Summary: The document includes a summary table that clearly lays out:
| Symbol | Name | Units | Meaning | Quantity | Equation | Relationship to Mass | | ------ | ----------------------- | ----------------- | ------------------------------------- | -------- | ----------------------- | ------------------------------------------------------------ | | g | Field strength | N/kg or m/s² | Gravitational force per unit mass | Vector | |g| = GM/r² | Force, F = GM₁M₂/r² = mg | | φ | Potential | J/kg | Gravitational potential energy per unit mass | Scalar | φ = -GM/r | Potential energy, U = -mGM/r = mφ | | | | | | | | | | | | | | | | | | | relationship between g and ϕ | | | | | g = - dφ/dr | | | relationship between F and U | | | | | F = - dU/dr | |

3. Practical Applications and Activities:

Simulation: The resource provides an embedded HTML5 applet simulation model (gravity07) at this link: https://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejss_model_gravity07/gravity07_Simulation.xhtml. This allows users to interact with the concepts and visualize the relationships between the variables by observing how the graphs of g and φ change with distance, among other options available in the applet.
ICT Inquiry Worksheet: The resource references "ICT inquiry worksheet 1 (E)" and "G field and potential' EJS", encouraging further investigation and exploration of the concepts. This indicates that this resource is meant to promote active learning rather than passive absorption of knowledge.
Other resources: There is an additional Java resource linked as http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejs/ejs_model_GField_and_Potential_1D_v8wee.jar, which provides a Java version of a similar simulation for the topics.

4. Target Audience & Educational Purpose:

The resource is designed for "Junior College" level physics education.
It aims to help students understand the relationships between:
Gravitational field strength and potential
Gravitational force and potential energy
How they relate to each other through mathematical differentiation.
The use of interactive simulations and worksheets promotes active learning and inquiry-based exploration.

5. Technical Details:

The simulation is built using the EasyJavaScriptSimulation (EJS) framework.
The simulations are accessible on a variety of devices (Android/iOS, Windows/MacOSX/Linux, ChromeBook).

6. Key Takeaways:

Gravitational field strength (g) is the negative gradient of gravitational potential (φ) with respect to distance, represented by g = -dφ/dr. This also indicates that g is a vector quantity pointing in the direction of decreasing gravitational potential.
Gravitational force (F) is the negative gradient of gravitational potential energy (U) with respect to distance, represented by F = -dU/dr.
These relationships highlight the interconnectedness of these fundamental gravitational concepts.
The resource facilitates conceptual understanding through visualisations, interactive simulations, and worksheets.

7. Conclusion:

This resource provides a valuable tool for teaching and learning the relationships between gravitational force, potential energy, field strength, and potential. By using a combination of mathematical descriptions, graphical representations, and interactive simulations, students can develop a deeper and more intuitive understanding of these concepts. The inclusion of activities reinforces the idea that understanding the relationships via observation and active investigation is crucial for internalizing the core concepts.

Gravitational Fields and Potentials Study Guide

Quiz

Instructions: Answer the following questions in 2-3 sentences each.

How are gravitational field strength (g) and gravitational potential (ϕ) related mathematically?
What does the negative sign in the equation g = -dϕ/dr indicate?
Explain the difference between gravitational field strength and gravitational potential.
What are the units for gravitational field strength and gravitational potential?
Is gravitational field strength a scalar or a vector quantity? Is gravitational potential a scalar or a vector quantity?
Describe the relationship between gravitational force (F) and gravitational potential energy (U).
How is the magnitude of the gravitational field strength calculated?
What does gravitational potential energy per unit mass refer to?
How would the graph of gravitational potential (ϕ) vs distance (r) appear around a point mass?
What is the significance of a simulation model in understanding these concepts?

Quiz Answer Key

Gravitational field strength (g) is the negative derivative of the gravitational potential (ϕ) with respect to distance (r). The equation g = -dϕ/dr expresses this relationship, showing how the rate of change of potential relates to the field strength.
The negative sign indicates that the gravitational field strength (g) points in the direction of decreasing gravitational potential (ϕ). This means that the force is directed towards the source of the gravitational field, or 'down' the potential gradient.
Gravitational field strength (g) is the force experienced per unit mass at a point in the field, while gravitational potential (ϕ) is the potential energy per unit mass at that point. g is a measure of the gravitational force; ϕ is a measure of the potential to do work due to gravity.
Gravitational field strength is measured in Newtons per kilogram (N/kg) or meters per second squared (m/s²), while gravitational potential is measured in Joules per kilogram (J/kg).
Gravitational field strength is a vector quantity, having both magnitude and direction. Gravitational potential is a scalar quantity, with magnitude only.
Gravitational force (F) is the negative derivative of gravitational potential energy (U) with respect to distance (r), expressed as F = -dU/dr. This equation reflects how the change in potential energy relates to the force experienced by a mass within the gravitational field.
The magnitude of the gravitational field strength (|g|) is calculated by G*M/r², where G is the gravitational constant, M is the mass of the source, and r is the distance from the source mass. The direction is toward the center of the source mass.
Gravitational potential energy per unit mass refers to the gravitational potential (ϕ), representing the potential energy a unit mass would possess at a particular point in a gravitational field. It indicates how much work could be done by gravity if a unit mass were moved to that location from a point of zero potential.
The graph of gravitational potential (ϕ) vs distance (r) would be a negative curve that approaches zero as r increases, indicating that potential increases with distance from the mass and will always be a negative value unless r is infinite. The curve steepens as r approaches 0, indicating that the potential energy decreases as the object gets closer to the central mass.
A simulation model provides a visual and interactive way to explore the relationships between these concepts, helping learners visualize how g and ϕ change with distance and allowing them to test different scenarios. The model can facilitate a deeper understanding beyond theoretical equations.

Essay Questions

Instructions: Answer the following questions in essay format. Consider including real world examples or scenarios.

Discuss the significance of understanding the relationship between gravitational field strength and gravitational potential for space exploration and satellite operations.
Compare and contrast the concepts of gravitational field strength and gravitational potential energy, paying particular attention to their similarities, differences, and practical applications.
Explain the mathematical derivation of the relationship between g and ϕ, elaborating on how differentiation links these two seemingly different quantities.
Using real world scenarios, describe how the sign and magnitude of gravitational potential influences motion within a gravitational field, especially noting cases of varying potential.
Critically evaluate the value and limitations of using simulation models to teach and understand concepts in gravitational physics.

Glossary of Key Terms

Gravitational Field Strength (g): The gravitational force experienced per unit mass at a specific point in space, measured in Newtons per kilogram (N/kg) or meters per second squared (m/s²). It is a vector quantity, with direction toward the source of the gravitational field.

Gravitational Potential (ϕ): The gravitational potential energy per unit mass at a specific point in space, measured in Joules per kilogram (J/kg). It is a scalar quantity that represents the work required to move a unit mass from a point of zero potential to that specific location.

Gravitational Potential Energy (U): The energy stored by an object due to its position within a gravitational field, measured in Joules (J). It is the potential to do work by moving within a gravitational field.

Derivative (dϕ/dr): The mathematical rate of change of gravitational potential (ϕ) with respect to distance (r), which is related to gravitational field strength. The derivative represents the slope of the graph of potential vs. distance.

Scalar Quantity: A physical quantity that has magnitude only (e.g., gravitational potential).

Vector Quantity: A physical quantity that has both magnitude and direction (e.g., gravitational field strength).

Test Mass (m): A hypothetical or real mass used to measure the gravitational field strength or potential at a specific location.

Source Mass (M): The mass that creates the gravitational field.

Distance (r): The radial distance from the center of the source mass to the location of interest in the field.

Simulation Model: A computer-based representation of a physical system that allows for interactive exploration and visualization of concepts.

Video

https://notebooklm.google.com/notebook/bb314f19-6d33-4d2f-a168-0219762425ad/audio

Other Resources

http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejs/ejs_model_GField_and_Potential_1D_v8wee.jar

Timeline of Main Events/Concepts

This source is not a historical narrative, but rather a description of a physics simulation and its related concepts. Therefore, the "events" are more like logical steps and development stages:

Establishment of Fundamental Relationships: The document begins by laying out the core mathematical relationships between gravitational field strength (g) and gravitational potential (ϕ), as well as between force (F) and potential energy (U).
Derivation of Key Equation: The core relationship of g = - dϕ/dr is derived by differentiating the potential function with respect to distance (r).
Conceptual Explanation: The negative sign in g = - dϕ/dr is explained using graphs, showing how the gradient of the potential affects the sign of the field strength.
Application to Force and Potential Energy: The relationship is then extended by multiplying by test mass (m), and F = - dU/dr is also established
Simulation Creation: A JavaScript HTML5 applet simulation model (gravity07) is developed. This allows users to visualize and interact with these relationships.
Worksheet Activity: An ICT inquiry worksheet and a EJS simulation are created for users to further explore and understand concepts.
Summary of Terms: The document includes a summary table that explicitly defines the relationship, meaning, and quantities for field strength (g) and potential (ϕ).
Model Deployment: The simulation is embedded for use on various platforms (web, mobile, etc.)

Cast of Characters

Anne Cox: Identified as a contributor to the project. Based on the credits, we can assume she contributed to the development or creation of this simulation, content, or resource.
Wolfgang Christian: Identified as a contributor to the project. Likely a key developer or co-developer of the Easy JavaScript Simulations (EJS) platform or specific resources related to the simulation.
Francisco Esquembre: Identified as a contributor to the project and according to the resources provided, has developed or co-developed the EJS framework along with other physics resources
Loo Kang WEE Lawrence aka lookang: User who has uploaded and created the content and the main maintainer of this website.

Frequently Asked Questions: Gravity, Potential, and Their Relationships

What is the relationship between gravitational field strength (g) and gravitational potential (ϕ)? The gravitational field strength (g) is related to the gravitational potential (ϕ) by the equation g = - dϕ/dr. This means the field strength is the negative rate of change of the gravitational potential with respect to radial distance (r). Mathematically, the derivative of ϕ with respect to r gives us the expression for g, which represents the force experienced per unit mass due to gravity.
How does the sign of the gradient of the potential (ϕ) vs. radius (r) graph relate to the sign of the gravitational field strength (g)? The gradient of the ϕ vs. r graph is the rate of change of potential with distance, or dϕ/dr. The gravitational field strength g is the negative of this gradient. Therefore, when the gradient of ϕ vs. r is positive, the corresponding value of g is negative, and vice-versa. This relationship highlights the direction of the force; that is, gravity pulls objects towards the source of the field.
What are the units of gravitational field strength (g) and gravitational potential (ϕ)? The gravitational field strength (g) is measured in Newtons per kilogram (N/kg) or equivalently in meters per second squared (m/s²). The gravitational potential (ϕ) is measured in Joules per kilogram (J/kg). These units reflect the definitions of the quantities: force per unit mass for g and potential energy per unit mass for ϕ.
How are gravitational force (F) and gravitational potential energy (U) related mathematically? The gravitational force (F) is related to the gravitational potential energy (U) by the equation F = - dU/dr. This equation is analogous to the g = - dϕ/dr relationship, but includes mass. The force F is the negative rate of change of the potential energy U with respect to radial distance r. This indicates that the force points in the direction of decreasing potential energy.
What is the physical interpretation of gravitational field strength (g)? Gravitational field strength (g) is the gravitational force experienced by a unit mass placed at that point in space. It is a vector quantity pointing towards the center of the source mass and indicates the strength and direction of the gravitational force at a given location.
What is the physical interpretation of gravitational potential (ϕ)? Gravitational potential (ϕ) represents the gravitational potential energy per unit mass at a particular location in space. It is a scalar quantity, and its value indicates how much energy is needed to move a unit mass from infinity to that specific point, with a negative sign indicating that the work is done by the gravitational field, as opposed to work done on the gravitational field.
What is the difference between gravitational field strength (g) and gravitational potential (ϕ) in terms of quantity types? Gravitational field strength (g) is a vector quantity, which means it has both magnitude and direction. Gravitational potential (ϕ), on the other hand, is a scalar quantity, meaning it has only magnitude and no direction. It's an important difference to consider when doing calculations and understanding the physics.
How can the equations g = -GM/r² and ϕ = -GM/r be used to understand the relationships between field strength and potential? The equations g = -GM/r² and ϕ = -GM/r show how the gravitational field strength and the gravitational potential, respectively, vary with distance from a source mass M. As the equations show, g varies with the inverse square of r, while ϕ varies inversely with r. It's also worth noting that if you mathematically differentiate ϕ with respect to r, you will obtain the same expression for g. Therefore, the two quantities are inter-related.