About

1.5 Example of investigate the motion of an oscillator using experimental and graphical methods

1.5.1.Q1: what is the maximum angle of release before the motion is not accurately described as a simple harmonic motion for the case of a simple free pendulum?

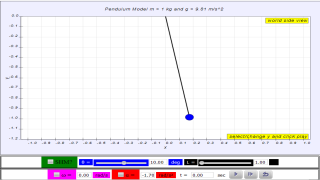
Example 1: Simple pendulum A pendulum bob given an initial horizontal displacement and released to swing freely to produce to and fro motion

1.5.2 Suggested Inquiry Steps:

1.     Define the question in your own words
2.     Plan an investigation to explore angle of release to record the actual period T and theoretical period  ${\displaystyle T_{the\text{or}y}=2\pi \sqrt{\frac{L}{g}}}$  where L is the length of the mass pendulum of mass, m and g is the gravitational acceleration of which the mass is experiencing, on Earth's surface  g = 9.81 m/s²
3.     A suggested record of the results could look like this   

angle / degree	T /s	Ttheory / s	${\displaystyle err\text{or}=\frac{(T-T_{the\text{or}y})}{T}100\%}$
05
10
15
20
30
40
50
60
70
80
90

 
        With the evidences collected or otherwise, suggests what the conditions of which the angle of oscillation can the actual period T be approximated to theoretical period such that  T  ≈ ${\displaystyle T_{the\text{or}y}=2\pi \sqrt{\frac{L}{g}}}$

1.5.3 Suggested Answer 1:

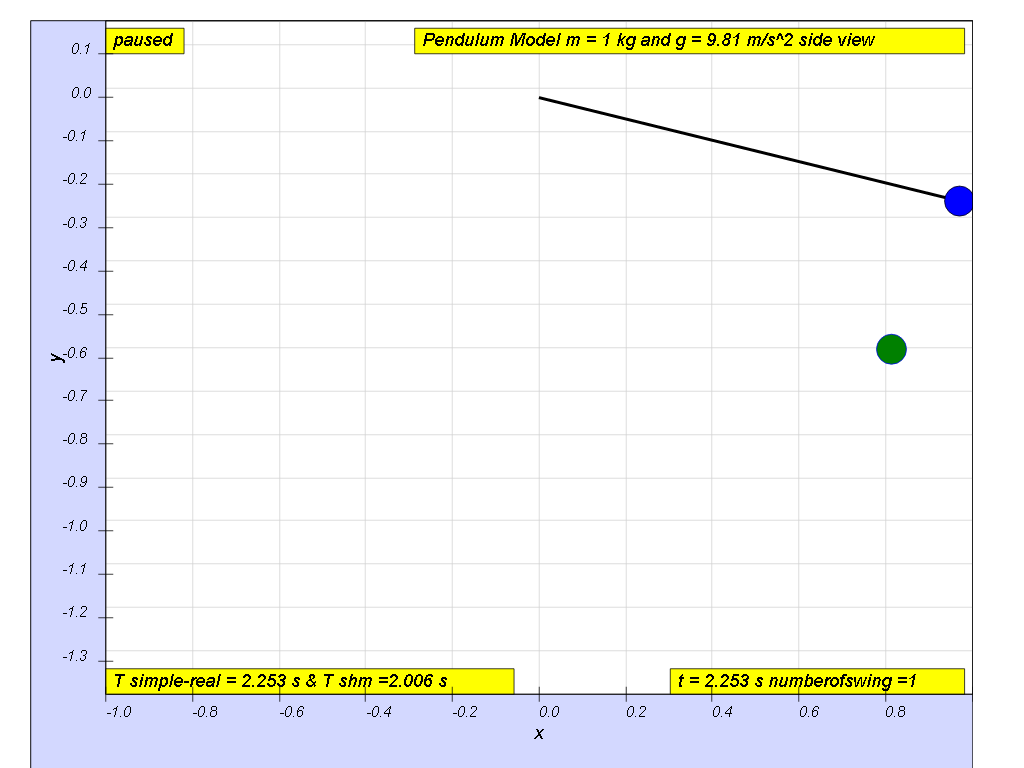
 angle θ  ≈ 10 degrees for ${\displaystyle err\text{or}=\frac{(2.010-2.006)}{2.010}\left(100\right)=0.2\%}$, depending on what is the error acceptable, small angle is typically about less than 10 degree of swing from the vertical.

1.5.4 Conclusion:

Motion approximates simple harmonic motion when the angle of oscillation is small < 10 degrees..

1.5.5 Other Interesting fact(s):

Motion approximates SHM when the spring does not exceed limit of proportionality during oscillations.

1.5.6 Real Life Application of Small Angle Approximations:

Astronomical applications of the Small Angle Approximation

1.5.7 YouTube

http://youtu.be/BRbCW2MsL94?t=2m16s This video shows many pendulums that goes in phase and out of phase with each other pendulum to creating a visually stunning effect.

1.5.8 Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/93

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM195/SHM195_Simulation.xhtml

Briefing Document: ⚛️Simple Harmonic Motion and Pendulum Oscillations

Subject: Analysis of "10.5 Example of investigation of motion of an oscillator using experimental and graphical method HTML5 Applet Simulation Model" from Open Educational Resources / Open Source Physics @ Singapore.

Date: October 26, 2024

1. Introduction:

This document provides a detailed analysis of a specific resource from Open Educational Resources / Open Source Physics @ Singapore. The resource, titled "10.5 Example of investigation of motion of an oscillator using experimental and graphical method HTML5 Applet Simulation Model", focuses on exploring the concept of Simple Harmonic Motion (SHM) using a pendulum as a model. It's designed as an interactive HTML5 applet suitable for various devices. The core idea revolves around the experimental investigation of a simple pendulum's motion and the limitations of the SHM approximation based on the angle of oscillation.

2. Main Themes and Key Ideas:

• Simple Harmonic Motion (SHM) and its Approximation: The primary focus of the resource is on the exploration of Simple Harmonic Motion (SHM). It emphasizes that real-world oscillatory motion, like that of a pendulum, often only approximates SHM under specific conditions.
• Quote: "Motion approximates simple harmonic motion when the angle of oscillation is small < 10 degrees." This statement highlights the condition for SHM approximation.
• Pendulum as a Model System: The document uses a simple pendulum as a concrete example to investigate SHM. The pendulum's motion is analyzed using both experimental data (through simulation) and theoretical calculations.
• Quote: "Example 1: Simple pendulum A pendulum bob given an initial horizontal displacement and released to swing freely to produce to and fro motion" This describes the setup for the pendulum experiment.
• Impact of Oscillation Angle: A key objective is to determine the maximum angle at which the pendulum's motion closely resembles SHM. The resource guides the user to experimentally test and discover this limit.
• Quote: "what is the maximum angle of release before the motion is not accurately described as a simple harmonic motion for the case of a simple free pendulum?" This is the central inquiry question.
• Experimental Investigation: The resource promotes an experimental approach where users are encouraged to:

1. Define the research question.
2. Plan an investigation (using the simulation).
3. Record the experimental data.
4. Compare experimental period (T) to the theoretical period (Ttheory).

• Theoretical vs. Experimental Period: The simulation allows users to compare the measured period of the pendulum swing with the theoretical period calculated using the standard SHM formula:
• T theory = 2π√(L/g), where L is the pendulum's length and g is the gravitational acceleration.
• Error Analysis: The resource emphasizes calculating and understanding the error between experimental and theoretical periods, helping users to understand deviations from the ideal SHM behavior.
• Quote: "e r r o r = ( T - T t h e or y ) T 100 %" describes the formula for calculating percentage error
• Small Angle Approximation: The key takeaway is that for the motion to approximate SHM, the angle of oscillation must be small (typically less than 10 degrees). This illustrates the concept of small angle approximations in physics.
• Quote: "angle θ ≈ 10 degrees for e r r o r = ( 2. 010 - 2. 006 ) 2. 010 ( 100 ) = 0. 2 % , depending on what is the error acceptable, small angle is typically about less than 10 degree of swing from the vertical."
• Real World Applications: The resource also alludes to real-world application of small angle approximation particularly in astronomy.
• SHM and Spring Systems: The resource also briefly notes that SHM approximation is also present in spring systems, so long as the spring is not stretched beyond its limit of proportionality.
• Quote: "Motion approximates SHM when the spring does not exceed limit of proportionality during oscillations."
• Interactive Simulation Model: The resource is not a static document but an interactive HTML5 simulation which allows for direct manipulation of the pendulum system and the observation of changes in the system's behavior.

3. Suggested Inquiry Steps:

The document outlines specific steps for inquiry which shows the intended educational use of the resource. The steps include:

1. Defining the question: users are expected to state the research question in their own words.
2. Planning the investigation: involves using the simulation to test the impact of the release angle
3. Recording results: the resource provides a sample table for recording data, which would allow for error calculation.
4. Concluding based on evidence: users are expected to identify and justify the maximum angle for SHM approximation.

4. Related Resources and Context:

The document also includes a large set of related resources, suggesting the wider scope of the project. Some of the associated material suggests that the platform offers more modules than just this isolated section, including a variety of models and simulations across topics like:

• Other examples of SHM, including spring systems
• Kinematics and dynamics
• Energy and gravitation
• Electromagnetism and waves
• Digital tools like Vernier calipers and micrometers
• Various interactive simulations for math and physics concepts

5. Target Audience:

The resource seems primarily targeted at secondary and junior college students studying physics and mechanics. The language, concepts, and experimental approach are all suitable for this level. The accessibility across various devices makes it adaptable to different learning environments.

6. Key Takeaways:

• The motion of a simple pendulum is a good model for understanding SHM, but its approximation is valid only for small angles of oscillation.
• This resource provides an interactive platform for students to explore SHM through experimentation, observation, and error analysis.
• The resource exemplifies the use of HTML5 applets to visualize complex physics concepts effectively.

7. Conclusion:

This resource offers a clear and interactive way for students to grasp the concept of Simple Harmonic Motion and its limitations. The emphasis on experimental investigation and data analysis makes it a valuable learning tool for students studying physics at the secondary and junior college level. The wide array of additional linked resources also illustrates the broader scope of the platform, emphasizing the use of interactive simulation as a means of learning.

Simple Harmonic Motion: A Study Guide

Quiz

1. What is the key condition for a pendulum's motion to be considered Simple Harmonic Motion (SHM)?
2. What is the practical limit for the angle of displacement of a pendulum for its motion to approximate SHM?
3. What formula is used to calculate the theoretical period of a simple pendulum?
4. What do the variables in the theoretical period formula stand for?
5. What does the simulation demonstrate in terms of the relationship between release angle and the accuracy of SHM approximations?
6. Briefly describe the purpose of the provided YouTube video.
7. Besides pendulums, what other system is mentioned that demonstrates approximate SHM under specific conditions?
8. What is the formula used to determine the percentage of error between theoretical and actual period?
9. Where can users access additional simulations and resources related to SHM?
10. Give one real-world example where the small angle approximation is applied.

Answer Key

1. The key condition is that the restoring force acting on the object is proportional to the displacement from its equilibrium position.
2. The angle of displacement must be less than approximately 10 degrees from the vertical for the motion of a pendulum to be considered SHM.
3. The formula for the theoretical period of a simple pendulum is Ttheory= 2π√(L/g).
4. In the formula, "L" represents the length of the pendulum and "g" represents the gravitational acceleration.
5. The simulation demonstrates that as the angle of release increases, the actual period of the pendulum deviates more from the theoretical period, meaning it no longer accurately approximates SHM.
6. The YouTube video demonstrates multiple pendulums swinging in and out of phase, creating a visually interesting effect.
7. Spring-mass systems exhibit approximate SHM as long as the spring does not exceed its limit of proportionality.
8. The percentage error is calculated as: error = (T-Ttheory) / T * 100%
9. Users can access additional simulations and resources through the provided links to the iwant2study.org website or the Google Play app.
10. Astronomical applications often use the small angle approximation.

Essay Questions

1. Discuss the relationship between experimental observation and theoretical models in the study of simple harmonic motion. How do simulations contribute to the understanding of this relationship?
2. Critically analyze the limitations of the simple pendulum model in representing real-world oscillatory motion. What factors are neglected, and how do they affect the accuracy of the model?
3. Explain the significance of the "small angle approximation" in the study of simple harmonic motion. What are the practical implications of this approximation and how does it simplify mathematical analysis?
4. Compare and contrast the use of experimental and graphical methods in investigating the motion of an oscillator. What are the strengths and weaknesses of each approach?
5. Considering the provided materials, design an experiment to further explore the conditions under which a system (e.g., a pendulum or spring-mass system) approximates Simple Harmonic Motion. Include detailed procedures, variables to be measured, and analysis of results.

Glossary of Key Terms

Simple Harmonic Motion (SHM): A type of periodic motion where the restoring force is directly proportional to the displacement and acts in the opposite direction.

Period (T): The time required for one complete cycle of oscillation.

Theoretical Period (Ttheory): The period of oscillation calculated using a mathematical formula, assuming ideal conditions.

Actual Period (T): The period of oscillation measured in a real-world setting or experiment.

Angle of Displacement (θ): The angle at which an object in SHM is displaced from its equilibrium position.

Small Angle Approximation: The approximation that for small angles (typically less than 10 degrees), sin θ ≈ θ (when θ is in radians), simplifying calculations involving SHM.

Restoring Force: A force that acts to bring an object back to its equilibrium position.

Limit of Proportionality: The point at which a spring or material no longer obeys Hooke’s Law.

 Apps

https://play.google.com/store/apps/details?id=com.ionicframework.shm195app415781&hl=en

FAQ: Exploring Oscillations and Simulations

• What is Simple Harmonic Motion (SHM) and what are some real-world examples of it? Simple Harmonic Motion (SHM) is a specific type of oscillatory motion where the restoring force is directly proportional to the displacement and acts in the opposite direction. In simpler terms, an object in SHM will move back and forth around an equilibrium point, with the force pulling it back towards the center getting stronger the farther away it is. Examples include a simple pendulum swinging through a small angle, a mass attached to a spring, and even certain aspects of how sound waves travel.
• How does the angle of release affect the motion of a simple pendulum? A simple pendulum's motion only closely approximates Simple Harmonic Motion (SHM) when its angle of release is small, typically less than 10 degrees from the vertical. At larger angles, the pendulum's period (time for one swing) deviates significantly from the theoretical value calculated assuming SHM. The restoring force is no longer directly proportional to the displacement, making the motion non-simple harmonic.
• What is the theoretical period of a simple pendulum and how is it calculated? The theoretical period (Ttheory) of a simple pendulum is calculated using the formula Ttheory = 2π√(L/g) , where 'L' is the length of the pendulum and 'g' is the acceleration due to gravity (approximately 9.81 m/s² on Earth). This formula is derived under the assumption of small angle oscillations (SHM), and its accuracy decreases with larger swing angles.
• What is the significance of the "small angle approximation" when studying oscillations? The "small angle approximation" (where the angle is less than 10 degrees) is crucial because it simplifies the mathematical description of pendulum motion. Within these small angles, the sine of the angle is approximately equal to the angle itself (in radians). This approximation allows us to use the simple formula for the period and treat the motion as Simple Harmonic Motion. Outside of these angles, the relationship is no longer linear, and motion becomes more complex.
• Beyond pendulums, where else might we see approximations of Simple Harmonic Motion? While the pendulum is a classic example, other systems approximate SHM if certain conditions are met. A mass attached to a spring will exhibit SHM if the spring does not exceed its elastic limit. These types of oscillations can be found throughout physics, engineering, and even fields like astronomy.
• What are the benefits of using simulations like the ones mentioned in the source for learning about oscillations? Interactive simulations like the ones discussed provide a dynamic and visual way to understand abstract concepts. Students can change parameters (such as mass, spring constant, angle of release) and observe their immediate effect on the system, often impossible in real life. These simulations support experimental investigation, data analysis, and visual representations, enhancing learning through active participation and exploration.
• What kind of educational resources are available on this website, besides physics simulations? This website offers a broad range of interactive educational resources spanning multiple disciplines, including Mathematics, English Language, and Geography. The resources feature tools such as quizzes, games, and simulations, making learning interactive and engaging for various age groups, from primary to junior college levels. Additionally, the platform includes simulations and tools related to scientific and math topics such as trigonometry, projectile motion, vectors, energy transfers and stores, and many others.
• Where can I find and run these simulations mentioned in the text? The simulations are available via web browsers on various platforms, including Windows, MacOSX, Linux, ChromeBook, and mobile devices including Android/iOS. The site also provides direct links to run them within web pages, such as via the provided iFrame code and Android app store links. You can start exploring directly from the main website and through the different subject tags, from the links provided on the website.