About

1.2.11 Example: Spring-mass system

 
A mass suspended from a spring, displaced vertically and released to move freely to produce up and down motion

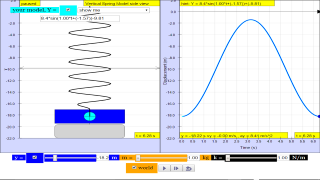
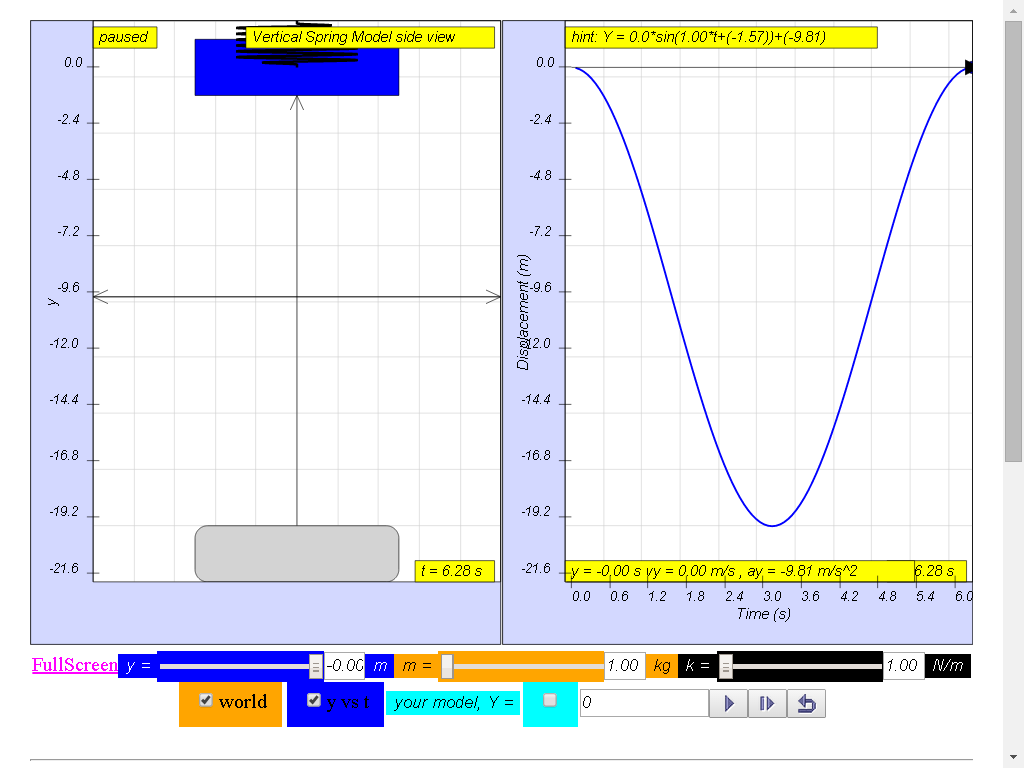
The model view of a mass suspended from a spring, displaced vertically and released to move freely to produce up and down motion with right panel showing the displacement, velocity and acceleration. 

Q1: under what conditions would this vertical spring mass system’s motion be not well modeled as a simple harmonic motion?

H1: the model assumes the restoring force by the spring is F = -ky, it is always correct for any magnitude of oscillation y in real springs. Is it always valid in the real spring motion when the spring is hyper extending beyond the linear limits of Hooke's Law ?

Q2: change the simulation y=0 m and Play the model. In the your model Y = _________, suggest your own suitable model that can describe the motion y.

Q3: in this same motion, propose the velocity and acceleration model(s)

Q4: carry out some other conditions, verify that the general equations for displacments if can be model by Y = Y₀sin(ωt+φ)+Y_shift where the usual symbols have the usual meaning. Hence or otherwise, Suggest with reasons, the meaning of Y₀ , ω , φ , and Y_shift.

Q5: similarly, suggest whether the model(s) for velocity, v_Y =ωY₀cos(ωt+φ) and

a_Y = - ω²Y₀sin(ωt+φ). Test them out using an example of your choice.

1.2.11.1 YouTube

http://youtu.be/P-Umre5Np_0 MIT Physics Demo -- Spray Paint Oscillator. A can of spray paint is attached to a spring oscillator. A roll of paper is run past the oscillating can. The result is a sine wave - http://en.wikipedia.org/wiki/Sine_wave - on the paper.Watch the original video on MIT TechTV - http://techtv.mit.edu/videos/803-spray-paint-oscillator

1.2.11.2 Tracker activity:

http://weelookang.blogspot.sg/2012/08/tracker-modeling-in-spring-mass-system.html

1.2.11.3 Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/90

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM161/SHM161_Simulation.xhtml

Briefing Document: ⚛️Vertical Spring-Mass Simulation Model

1. Overview

This document reviews the resource "10.2.11 Example Vertical Spring Mass JavaScript HTML5 Applet Simulation Model" from the Open Educational Resources / Open Source Physics @ Singapore website. This resource provides an interactive simulation of a mass-spring system oscillating vertically and aims to facilitate understanding of Simple Harmonic Motion (SHM) and related concepts. The simulation is accessible on various platforms (Android/iOS, Windows/MacOSX/Linux, ChromeBook Laptops) and is embedded within a webpage using an iframe. The page includes questions that prompt the user to explore key concepts in SHM. It also provides links to other relevant resources and simulations.

2. Key Themes and Ideas

• Interactive Simulation of Vertical Spring-Mass System: The core of the resource is a simulation showing the vertical oscillatory motion of a mass suspended from a spring. Users can observe the motion and the graphs of displacement, velocity and acceleration, allowing for a visual and dynamic understanding of the system.
• Quote: "A mass suspended from a spring, displaced vertically and released to move freely to produce up and down motion... with right panel showing the displacement, velocity and acceleration."
• Exploration of Simple Harmonic Motion (SHM): The resource implicitly focuses on SHM. The questions in the text guide users to think about whether a spring-mass system perfectly follows SHM and what parameters can affect this.
• Conditions for SHM Validity: The first question directly addresses the limitations of the SHM model, specifically asking under what conditions the motion may not be well modeled as SHM. This prompts users to consider the real-world behavior of springs and to understand that the linear model (Hooke's Law: F = -ky) has limitations, particularly for large oscillations.
• Quote: "H1: the model assumes the restoring force by the spring is F = -ky, it is always correct for any magnitude of oscillation y in real springs. Is it always valid in the real spring motion when the spring is hyper extending beyond the linear limits of Hooke's Law ?"
• Mathematical Description of Motion: The resource encourages students to develop and verify equations for displacement, velocity, and acceleration related to the vertical spring mass system motion, in terms of Y0, ω , φ , and Yshift, which are, respectively, amplitude, angular frequency, phase constant and vertical shift of the center position of oscillation.
• Quote: "carry out some other conditions, verify that the general equations for displacments if can be model by Y = Y0sin(ωt+φ)+Yshift where the usual symbols have the usual meaning."
• Use of Interactive Simulations for Learning: The resource highlights the value of interactive simulations for visualizing abstract concepts in physics. By allowing users to manipulate parameters and observe the results, it encourages active learning. The simulation can be embedded in webpages so students have easy access to play with parameters.
• Links to External Resources: The page also includes links to a YouTube video of an MIT Physics Demo (Spray Paint Oscillator) which demonstrates how the simple harmonic motion creates a sine wave, and a link to a Tracker activity, which can further help students to do investigations using the simulation.
• Parameter Adjustments: The 'Other Resources' section mentions that students can explore how changing various parameters (gravity, spring constant, starting distance, and mass) affects the period of the motion, and examine the influence of damping. This hands-on approach helps to enhance learning.
• Quote: "Change each variable – gravity, spring constant, starting distance and mass – and observe how each one affects the period. Can you explain why?"
• Comparisons to Other Systems: The resource guides exploration of a spring pendulum model, where the spring also allows a pendulum motion in addition to the SHM in the vertical direction. This allows students to relate the concepts explored in this simulation to other oscillatory systems.
• Quote: "Can you distinguish the pattern of spring motion (up and down) from the pattern of pendulum motion (back and forth)? How are the two related?"
• Educational Resource Platform: This resource is part of a much larger collection of open-source physics and mathematics education materials. The sheer number of other resources listed is an indication of the breadth of topics covered, ranging from basic mechanics, electromagnetism, to computational models.

3. Specific Questions and Their Purpose

The questions included in the text are designed to guide students' exploration and understanding:

• Q1: Under what conditions would this vertical spring mass system’s motion be not well modeled as a simple harmonic motion?Purpose: Promotes critical thinking about the limitations of models and introduces the concept of real-world deviations from idealized systems.
• Q2: change the simulation y=0 m and Play the model. In the your model Y = _________, suggest your own suitable model that can describe the motion y.Purpose: Forces the student to explore the simulation and start connecting the motion with its mathematical equation
• Q3: in this same motion, propose the velocity and acceleration model(s)Purpose: Asks the students to explore the mathematical equations of the motion
• Q4: carry out some other conditions, verify that the general equations for displacements if can be model by Y = Y0sin(ωt+φ)+Yshift where the usual symbols have the usual meaning. Hence or otherwise, Suggest with reasons, the meaning of Y0 , ω , φ , and Yshift.Purpose: Facilitates a deeper understanding of the parameters that affect the motion and also verify a general formula of the displacement of the spring mass system in the vertical direction.
• Q5: similarly, suggest whether the model(s) for velocity, vY =ωY0cos(ωt+φ) and aY = - ω2Y0sin(ωt+φ). Test them out using an example of your choice.Purpose: Further encourages students to explore equations in SHM by suggesting them to formulate a model for the velocity and acceleration.

4. Implications for Education

This resource is a valuable tool for educators:

• Active Learning: The interactive nature of the simulation promotes active learning and deeper engagement with the material.
• Conceptual Understanding: The resource focuses on conceptual understanding of the physics behind the SHM model.
• Flexibility: The platform-agnostic nature of the simulation makes it accessible for use in various learning environments.
• Inquiry-Based Approach: The questions encourage an inquiry-based approach to learning, prompting students to explore and explain phenomena themselves.
• Integration with Other Resources: The links to additional resources provide an opportunity to make cross-connections with other topics.

5. Conclusion

The "10.2.11 Example Vertical Spring Mass JavaScript HTML5 Applet Simulation Model" provides a well-designed and interactive simulation for learning about simple harmonic motion and the dynamics of a vertical spring-mass system. Its strengths lie in its accessibility, interactive nature, and the thoughtful questions that prompt critical thinking. The large list of other resources on the website is an indication of the depth of material available on the site and could be a valuable resource for educators and students alike.

Vertical Spring Mass System Study Guide

Quiz

Instructions: Answer the following questions in 2-3 complete sentences each.

1. Under what specific condition, related to the spring's behavior, would a vertical spring-mass system not be accurately modeled by simple harmonic motion (SHM)?
2. In the provided simulation, when the initial displacement (y) is set to 0 meters, what is the resulting motion, and suggest a way to model this motion mathematically?
3. For a vertical spring-mass system exhibiting SHM, what are the general mathematical models for velocity and acceleration?
4. The general equation for displacement in SHM is often given as Y = Y₀sin(ωt+φ)+Yshift. In this context, define Y₀, ω, φ, and Yshift.
5. How are the models for velocity and acceleration related to the model of displacement? Use your own example for testing out the equations.
6. According to the text, how can the period of a spring-mass system be determined using the simulation's graph?
7. Besides spring constant and mass, what other variables in the simulation can affect the period of a spring-mass system?
8. The simulation also shows a pendulum on a spring. How does its motion differ from that of a mass oscillating on just a spring?
9. What happens to the energy when the pendulum on a spring switches between back-and-forth and up-and-down motions?
10. Based on the text, what is the purpose of using "Tracker activity" with regards to the spring-mass system?

Quiz Answer Key

1. Simple harmonic motion assumes that the restoring force of the spring is linear and always accurately described by Hooke's Law (F = -ky). However, when the spring extends beyond its linear limits, particularly at large oscillations, this assumption breaks down because the restoring force becomes nonlinear which will make the system not experience simple harmonic motion.
2. When y = 0 m, there is a resting motion which is also called the equilibrium position. This motion can be modeled mathematically as y = 0 at all values of time (t), unless it is given an initial push with the variable initial velocity.
3. For simple harmonic motion, the velocity (v) model is generally given by vY = ωY₀cos(ωt+φ) and the acceleration (a) model is generally given by aY = -ω²Y₀sin(ωt+φ). These models represent the first and second derivatives of the displacement equation, respectively, with respect to time.
4. Y₀ represents the amplitude of the oscillation, or the maximum displacement from the equilibrium position; ω is the angular frequency, determining the rate of oscillation; φ is the phase constant, indicating the starting point of the oscillation cycle; and Yshift represents a vertical shift in the equilibrium position of the motion.
5. The models for velocity and acceleration are the first and second derivatives of the displacement model with respect to time. For instance, if we have Y = 5sin(2t), then vY = 10cos(2t) and aY = -20sin(2t).
6. The period of a spring-mass system can be determined by observing the graph of the mass's height over time in the simulation. The period is the time it takes for the mass to complete one full up-and-down cycle.
7. Besides spring constant and mass, the simulation allows for changes in gravity and initial displacement. These variables can influence the period of a spring-mass system (gravity indirectly through its effect on the equilibrium position), which shows that the system will have period equal to 2pisqrt(m/k), and neither displacement or gravity will affect it.
8. The motion of a pendulum on a spring combines the back-and-forth movement of a pendulum with the up-and-down movement of a spring. This results in a more complex motion pattern than either system exhibits in isolation.
9. When the pendulum switches between back-and-forth and up-and-down motions, there is a continuous transfer of energy between the potential and kinetic energies. Sometimes, the energy is stored in the back and forth motion, while other times the energy will be mainly stored in the up and down motion.
10. Tracker activity, with the provided web link, allows for a visual analysis and modeling of the system's motion. By using software to track the position of an object in a video, we can compare real-world motion with the theoretical model of the simulation.

Essay Questions

Instructions: Answer each of the following questions in essay format.

1. Discuss the limitations of modeling a real-world spring-mass system using simple harmonic motion and describe scenarios where the model may become invalid.
2. Compare and contrast the factors affecting the period of a simple pendulum versus those affecting the period of a vertical spring-mass system.
3. Analyze the interplay between potential and kinetic energy in the combined pendulum-spring system, explaining the transfer and transformation of energy within the system.
4. Describe the role of simulations in physics education and discuss how the provided simulation can be used to enhance the learning process of the vertical spring-mass system.
5. Explain in what ways simulations can become helpful tools, but what are their limitations and ways to deal with those limitations.

Glossary of Key Terms

Amplitude (Y₀): The maximum displacement of the oscillating mass from its equilibrium position in simple harmonic motion (SHM).

Angular Frequency (ω): A measure of the rate of oscillation, related to the frequency (f) by the equation ω = 2πf. It determines how quickly the system cycles.

Displacement (y): The position of the mass relative to its equilibrium position at any given time.

Equilibrium Position: The position where the mass would rest if undisturbed. For a vertical spring, this is the point where the spring's restoring force balances gravity.

Hooke's Law: A law stating that the force exerted by a spring is proportional to its displacement from its equilibrium length, given by F = -ky.

Oscillation: A repetitive back-and-forth or up-and-down movement of an object.

Period (T): The time it takes for one complete cycle of oscillation to occur.

Phase Constant (φ): A value that determines the initial position of the oscillation in its cycle at time t=0.

Restoring Force: The force that acts to return a displaced object to its equilibrium position, such as the spring's force in a spring-mass system.

Simple Harmonic Motion (SHM): A type of periodic motion in which the restoring force is directly proportional to the displacement and acts in the opposite direction, resulting in sinusoidal motion.

Spring Constant (k): A measure of the stiffness of a spring; a higher value of k indicates a stiffer spring.

Vertical Shift (Yshift): In the displacement equation, represents the displacement of the equilibrium position from a defined zero point.

Other Resources

 

 

FAQ on Vertical Spring-Mass System Simulations

1. Under what conditions would the vertical spring-mass system's motion not be well-modeled as simple harmonic motion (SHM)?
2. The provided model assumes that the restoring force of the spring always follows Hooke's Law (F = -ky). However, real springs have a limit to the displacement where they no longer behave linearly. If the spring is stretched or compressed too much (hyper-extended) beyond these limits, Hooke's Law will no longer accurately model its behavior. This means the restoring force will deviate from the linear relationship with displacement, and the motion will no longer be accurately described as simple harmonic. Factors such as spring coil touching and the spring reaching material limits of extension can come into play, for example, the spring material becomes permanently deformed.
3. If the simulation starts with the mass at y = 0 meters, what is a suitable model to describe the subsequent motion?
4. Starting at y = 0 m would be the equilibrium position of the spring, meaning the spring is not stretched or compressed (assuming no gravitational force is acting). If the mass starts at equilibrium, the model depends on initial conditions such as velocity. If it starts at zero velocity, no motion will occur. If it starts with some initial velocity, it will oscillate. The motion of the mass can still be described using the general equation for simple harmonic motion: y = Y₀sin(ωt + φ) + Yshift, where Y₀ represents the amplitude of oscillation, ω is the angular frequency, t is time, φ is the phase constant, and Yshift is the vertical shift relative to equilibrium, which will be zero in the case where 0m is also the equilibrium length. It’s important to define this starting position to define the phase constant.
5. How can we model the velocity and acceleration of the mass in this system?
6. Assuming the motion of the mass is described by y = Y₀sin(ωt + φ) + Yshift, the velocity (vY) and acceleration (aY) can be modeled as derivatives of the displacement with respect to time. The velocity model is the first derivative of y, which would be: vY = ωY₀cos(ωt + φ). The acceleration model is the second derivative of y, or the derivative of the velocity, which would be: aY = -ω²Y₀sin(ωt + φ). These equations represent the sinusoidal nature of velocity and acceleration in SHM, with the acceleration being proportional to the negative of the displacement, a defining feature of simple harmonic motion.
7. Explain the meaning of Y₀, ω, φ, and Yshift in the general displacement equation Y = Y₀sin(ωt + φ) + Yshift.

• Y₀ (Amplitude): Represents the maximum displacement of the mass from its equilibrium position. It indicates the extent of the oscillation.
• ω (Angular Frequency): Represents how quickly the oscillation occurs. It's related to the frequency (f) by the equation ω = 2πf, where the frequency is the number of cycles of motion in a unit of time. The period is T = 2π/ω
• φ (Phase Constant): Determines the initial position of the mass at time t=0. It’s also referred to as the phase shift or the initial phase. If it's 0, then it starts at the equilibrium position; if it's π/2, it starts at the maximum displacement, and so on.
• Yshift (Vertical Shift): Represents any vertical shift in the equilibrium position from the reference point (zero displacement). This can be the static stretch of the spring caused by the mass. Typically, if y=0 is defined as the equilibrium point, Yshift is also zero.

1. Are the proposed velocity (vY = ωY₀cos(ωt+φ)) and acceleration (aY = -ω²Y₀sin(ωt+φ)) models correct? How can we verify this?
2. Yes, the proposed models are generally correct for simple harmonic motion, derived as first and second derivatives of the displacement equation. The models describe the time dependence of velocity and acceleration in relation to displacement in SHM. They correctly show that when displacement is at maximum (y=Y₀), velocity is zero and acceleration is maximum in the opposite direction (a=-ω²Y₀), and when the displacement is zero, velocity is maximum and acceleration is zero. To verify the models:
3. Simulation: Run simulations using different initial conditions (Y₀, ω, and φ) and measure the maximum velocity, maximum acceleration, and the timing of changes between velocity and acceleration, and compare these with the model predictions.
4. Tracker Software: Use video analysis software (like Tracker) to track the mass's position, calculate velocities, and compare data with the model equations, as mentioned in one of the sources.
5. Graphs Use the simulation's graph features to visually inspect the relationships between displacement, velocity, and acceleration, and verify that they follow the predicted sinusoidal patterns, with velocity being a cosine function when displacement is sine, and acceleration having an opposite sign to the displacement.
6. How do variables like gravity, spring constant, mass, and initial displacement affect the period of oscillation in the spring-mass system?

• Gravity: Gravity, in this case, affects the equilibrium point of the system, causing the spring to stretch more when the mass is attached. While it changes the location of equilibrium (Yshift), gravity does not alter the period of oscillation. The time it takes for the mass to complete an up-and-down cycle is not changed by gravity.
• Spring Constant (k): A higher spring constant (stiffer spring) will result in a shorter period, as the restoring force is greater. The period is inversely proportional to the square root of the spring constant.
• Mass (m): A larger mass will increase the period of oscillation. The period is directly proportional to the square root of the mass. The specific relationship is T = 2π√(m/k).
• Starting Displacement: This refers to how far the mass is initially pulled or pushed away from the equilibrium. Starting displacement has no effect on the period of oscillation as long as the motion is linear SHM. It will, however, directly affect the amplitude.

1. How does damping affect the period of the spring-mass system's motion?
2. Damping, which is a force that dissipates energy in the system, does not change the period of oscillation in a spring-mass system. Damping does, however, reduce the amplitude of the oscillation, and thus the total mechanical energy decreases over time. If the damping is too strong, the system might not even oscillate. The period is determined by the mass and the spring constant and, therefore, is not influenced by the presence of damping.
3. How does the motion of a spring pendulum differ from a simple spring-mass system, and how are the two types of motion related?
4. A simple spring-mass system exhibits motion along one axis. When a pendulum is also attached, there are now two axes of motion. The spring-pendulum system can exhibit a combination of both vertical (spring-like) and horizontal (pendulum-like) motion, and energy may transfer between these two modes. The graphs show motion in two directions, and energy can switch between back-and-forth (pendulum) and up-and-down (spring) depending on initial conditions. The motion is complex and can create patterns of motion where energy switches between these different axes, depending on factors such as gravity, rod length, spring constant, mass, and the initial starting angle or position. In some cases there will be a very complex pattern, but when the spring motion is very small, the system is very similar to a pendulum, and when the pendulum motion is very small, it becomes a simple spring-mass system.