About

1.4 (b)    Variation with Displacement of Energy in Simple Harmonic Motion

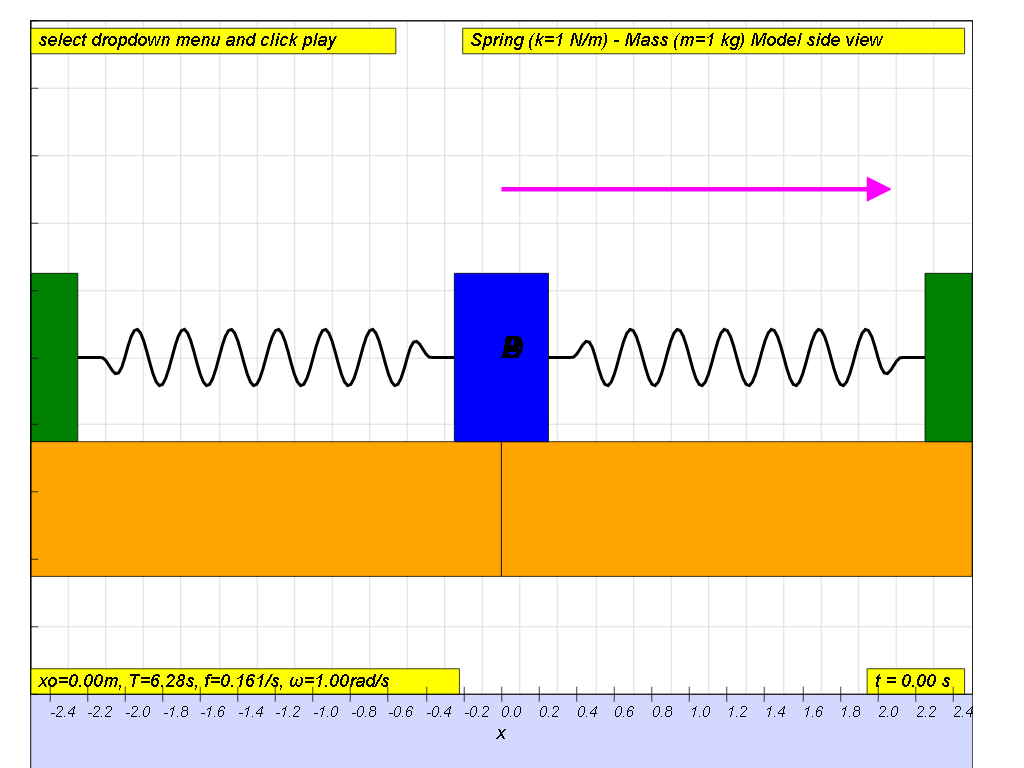
Consider a spring of spring constant k connected to a mass m as shown. When the mass is displaced from its equilibrium position by some speed, it will oscillate to the right and left.
 


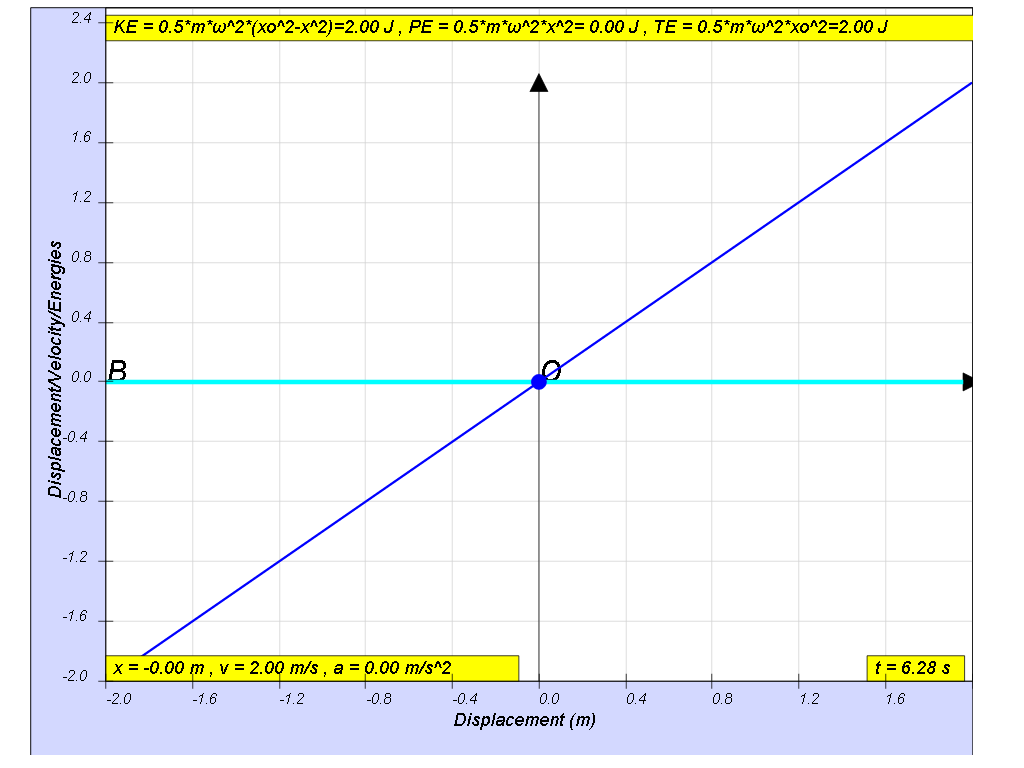
At the beginning x=0, t = 0, the energy of the system will consist totally of the mass spring’s kinetic energy (KE).
From 0 < t < T/4, as the mass moves away from x = 0, the spring pulls the mass towards equilibrium position, this KE is converting to PE as stored spring potential energy.
At the maximum amplitude, x = x₀, t = T/4, the all the energy of the system will consist totally of the spring’s potential energy (PE).
From T/4 < t < T/2 as the mass moves towards x = 0, the spring pulls the mass toward the equilibrium position, the potential energy is transformed back into kinetic energy (KE) until at the equilibrium position the kinetic energy will reach a maximum.
similarly, from T/2 < t < 3T/4, the similar energy conversion occurs but now for negative values of x moving away from equilibrium position .
similarly, from  3T/4 < t < T, the similar energy conversion occurs but now for negative values of x moving towards equilibrium position .

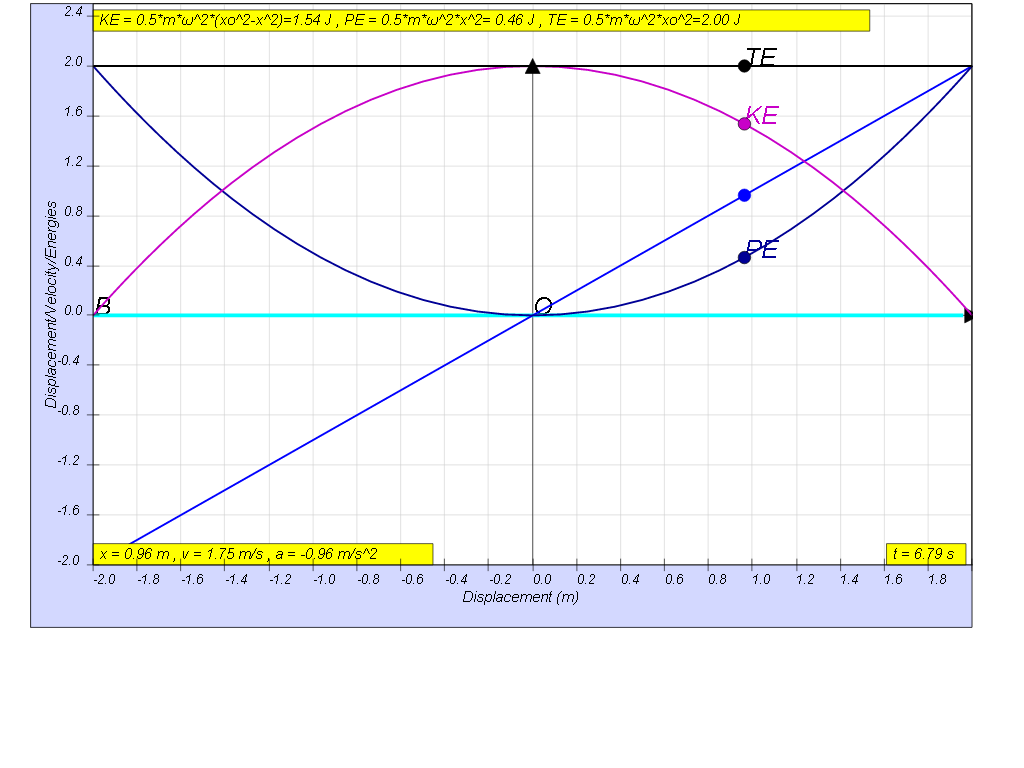
The constant exchange between potential energy PE and kinetic energy KE is essential in maintaining oscillations. The total energy TE, which is the summation of kinetic and potential energy, will always add up to a constant value as shown.





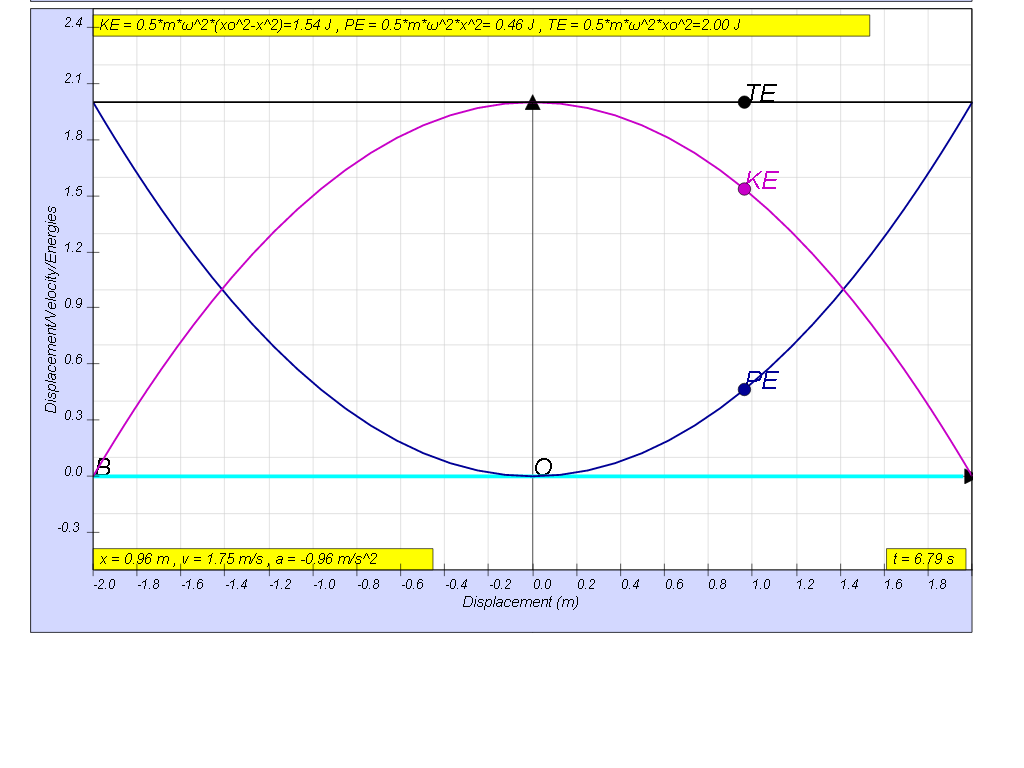
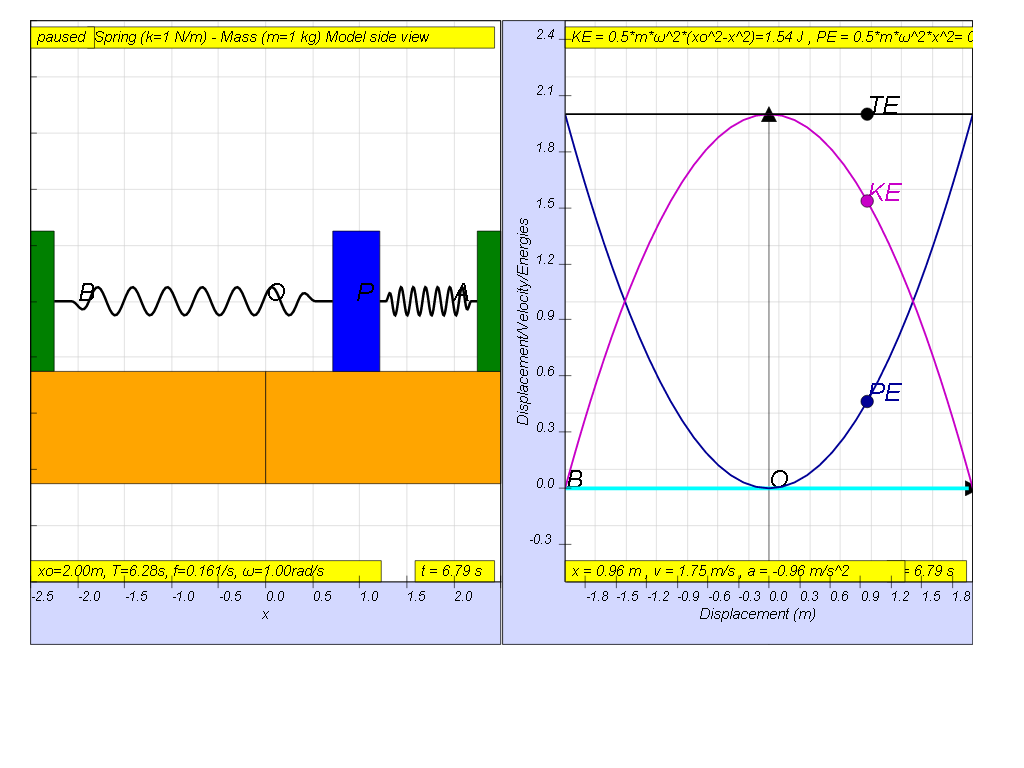
this is how the x vs x looks together of the energy vs x graphs



recalling Energy formula

KE = ½ m v²
PE =  ½ k x² therefore, total mechanical energy TE is both KE and PE, can be written as

TE = KE + PE = ½ m v² + ½ k x²
since  $v=\pm \sqrt{(x_0^2-x^2)}$

KE = ½ m v² = ½ m ω²( x_o²- x²)

from the simple harmonic motion, we also can get $\omega =\sqrt{\genfrac{}{}{0.1ex}{}{k}{m}}$

PE =  ½ k x² = ½ m ω²x²

therefore,

TE = KE + PE = ½ m ω²( x_o²- x²) + ½ m ω²x² = ½ m ω²x₀²

hence or otherwise the table below shows the various formula and their values

1.4.1 Summary

general energy formula	SHM energy formula	when x = -x0	when x = 0	when x = x0
KE = ½ m v2	KE = ½ m ω2( xo2- x2)	0	½ m ω2x02	0
PE =  ½ k x2	PE = ½ m ω2x2	½ m ω2x02	0	½ m ω2x02
TE = KE + PE	TE = ½ m ω2( xo2- x2) + ½ m ω2x2	½ m ω2x02	½ m ω2x02	½ m ω2x02

If no energy is lost during an oscillation, then total energy remains constant.

1.4.2 Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/81

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM18/SHM18_Simulation.xhtml

Briefing Document: ⚛️Simple Harmonic Motion and Energy Variation

Subject: Analysis of the "10.4(b) Variation with displacement of energy in simple harmonic motion JavaScript HTML5 Applet Simulation Model" resource from Open Educational Resources / Open Source Physics @ Singapore.

Date: October 26, 2024

1. Introduction:

This document analyzes a resource focused on the energy transformations within Simple Harmonic Motion (SHM), specifically a mass-spring system. The resource is a JavaScript HTML5 Applet simulation model designed for educational purposes, allowing users to visualize and understand the dynamic interplay between kinetic energy (KE) and potential energy (PE) during oscillations. It is intended for use across various platforms (desktops, laptops, tablets and mobiles) in learning institutions, including Junior Colleges. The simulation is designed with easy manipulation in mind.

2. Core Concepts:

• Simple Harmonic Motion (SHM): The resource explores SHM using a mass-spring system as a model. This system exhibits oscillatory motion around an equilibrium point.
• Energy Conservation: The fundamental principle highlighted is that in an ideal system without energy loss (e.g., friction), the total mechanical energy (TE) remains constant. This TE is the sum of the kinetic energy (KE) and potential energy (PE) of the system.
• Energy Transformation: During SHM, there's a constant conversion between KE and PE:
• When the mass passes through the equilibrium position, kinetic energy is at its maximum and potential energy is zero.
• When the mass is at maximum displacement (amplitude), potential energy is at its maximum, and kinetic energy is zero.
• As the mass moves away from the equilibrium, KE is converted into PE and vice versa.
• Mathematical Relationships: The document presents the relevant formulas relating KE, PE, and TE, displacement (x), velocity (v) and angular frequency (ω)
• KE = ½ mv²
• PE = ½ kx²
• TE = KE + PE = ½ m v² + ½ k x²
• v = ± ω sqrt(x0²-x²) where x0 is the amplitude
• KE = ½ m ω² (x0² - x²)
• PE = ½ m ω²x²
• TE = ½ m ω² x0²

3. Key Ideas and Facts:

• Initial Conditions: At the beginning of the simulation (t=0, x=0), the system possesses total kinetic energy and zero potential energy.
• Energy at Maximum Displacement: At maximum displacement (x=x0, t=T/4), all energy is in the form of potential energy.
• Energy at Equilibrium: At the equilibrium position (x=0, t = T/2 or T or any integer multiple of T/2), all energy is kinetic.
• Constant Total Energy: "The total energy TE, which is the summation of kinetic and potential energy, will always add up to a constant value." This constant value is ½ m ω² x0²
• Summary Table: A table summarizes the KE, PE, and TE formulas, along with their values at different displacements (x = -x0, x = 0, x = x0). This table clearly illustrates the energy variations at key positions.
• Simulation Model: The resource links to a simulation that allows users to observe these energy transformations in real time.
• Multiple Contexts: The page is embedded with many learning apps and links including related simulations and other learning resource on various topics. This is a resource page for educational use.

4. Important Quotes:

• "At the beginning x=0, t = 0, the energy of the system will consist totally of the mass spring’s kinetic energy (KE)."
• "At the maximum amplitude, x = x0, t = T/4, the all the energy of the system will consist totally of the spring’s potential energy (PE)."
• "The constant exchange between potential energy PE and kinetic energy KE is essential in maintaining oscillations."
• "If no energy is lost during an oscillation, then total energy remains constant."

5. Educational Implications:

• Visual Learning: The applet allows a visual understanding of the energy changes during SHM. This helps to better understand the abstract concepts.
• Interactive Learning: Users can manipulate the simulation, allowing for a more interactive and engaging learning experience.
• Formula Application: The resource provides formulas which are then applied within the simulation to verify the principle of conservation of energy.
• Conceptual Understanding: By visualizing how KE and PE transform, the resource strengthens conceptual understanding of SHM and energy conservation.
• Versatile Application: The resource can be accessed on a variety of platforms, making it widely accessible for educational use in various settings.

6. Additional Resources:

The page includes links to a multitude of other interactive simulations related to physics and mathematics. This highlights a wider context for the main content, indicating a larger collection of educational resources.

7. Conclusion:

The "10.4(b) Variation with displacement of energy in simple harmonic motion" resource provides a valuable educational tool for understanding the dynamics of simple harmonic motion and the conservation of energy. The simulation is complemented with clear explanations, mathematical relationships, and a summary table, making it a comprehensive and effective learning aid. The wide range of supporting materials and interactive tools on the site enhances its value as a tool for teachers and students.

This briefing document offers a detailed look at the resource's purpose, contents, and educational implications.

 

Simple Harmonic Motion Energy Study Guide

Quiz

1. Describe the energy transformation in a simple harmonic motion (SHM) system as it moves from the equilibrium position to the maximum amplitude.
2. At which point in the SHM cycle is the kinetic energy (KE) at its maximum value, and what is the corresponding value for potential energy (PE)?
3. What does it mean for the total energy (TE) of a simple harmonic oscillator when there are no energy losses due to friction or other factors?
4. Explain the relationship between displacement and potential energy in a spring-mass system undergoing SHM, using a formula.
5. What is the value of the kinetic energy when the mass in SHM reaches its maximum displacement?
6. How can the angular frequency (ω) of the SHM be expressed in terms of the spring constant (k) and the mass (m) attached to the spring?
7. In an ideal SHM system, describe the energy conversion during the entire cycle of motion starting from the equilibrium position.
8. If the mass of a simple harmonic oscillator increases, what happens to the total energy of the system, assuming the initial amplitude and frequency remain the same?
9. What happens to the speed of the mass as it moves from a point of maximum displacement to the equilibrium point?
10. How do the provided equations demonstrate the conservation of mechanical energy in SHM?

Quiz Answer Key

1. As the mass moves away from the equilibrium position, its kinetic energy (KE) is converted into potential energy (PE) stored in the spring. At the maximum amplitude, all the energy is stored as PE.
2. The kinetic energy (KE) is at its maximum value at the equilibrium position (x=0). At this point, the potential energy (PE) is zero.
3. When there are no energy losses, the total energy (TE) remains constant throughout the oscillation. It is the sum of KE and PE at any given point in the cycle.
4. The potential energy (PE) is directly proportional to the square of the displacement, shown by the formula PE = ½ kx², where k is the spring constant and x is the displacement.
5. The kinetic energy is zero when the mass is at its maximum displacement as at that point, the velocity is momentarily zero before reversing direction.
6. The angular frequency (ω) can be expressed as the square root of the spring constant divided by the mass: ω = √(k/m).
7. Starting from the equilibrium position, KE is maximum, and PE is zero. As the mass moves towards maximum amplitude, KE is converted to PE. At max amplitude, KE is zero, PE is max. Then, as the mass returns toward equilibrium, PE is converted back to KE and the cycle continues with PE back to zero.
8. An increase in mass will not change the total energy if the initial amplitude and frequency are the same. Total energy in SHM is 1/2momega^2*xo^2, where m is mass, omega is angular frequency, and xo is amplitude. If amplitude and frequency remain constant, a change to the mass will not affect the energy.
9. The speed of the mass increases as it moves from the point of maximum displacement to the equilibrium point, since potential energy is converted to kinetic energy.
10. The total energy equation, TE = ½ m ω²( xo²- x²) + ½ m ω²x² = ½ m ω²x₀², shows that the sum of kinetic and potential energy is always constant and equals ½ m ω²x₀², irrespective of the displacement, proving that energy is neither gained nor lost in the system.

Essay Questions

1. Discuss in detail the relationship between kinetic energy, potential energy, and total energy in a simple harmonic motion system. How do these energies change with displacement?
2. Explain the concept of energy transformation in SHM. Using the provided equations, detail how mechanical energy is conserved during oscillations.
3. Describe how the various parameters (mass, spring constant, amplitude) of a simple harmonic oscillator affect its energy, including kinetic and potential energy.
4. Compare and contrast the energy dynamics of a simple harmonic oscillator at different points in its cycle, including the equilibrium position, maximum positive displacement, and maximum negative displacement.
5. Using examples, describe a simple harmonic motion system and how to model the energy of this system using the provided equations, including both mathematical and conceptual descriptions.

Glossary of Key Terms

• Simple Harmonic Motion (SHM): A type of periodic motion where the restoring force is directly proportional to the displacement and acts in the opposite direction. It results in oscillations about an equilibrium position.
• Kinetic Energy (KE): The energy of motion, calculated as ½ * m * v², where m is mass and v is velocity. In SHM, KE is maximal at the equilibrium position and zero at maximum displacement.
• Potential Energy (PE): Energy stored within a system due to its position or configuration. In SHM involving a spring, it is stored in the spring and calculated as ½ * k * x², where k is the spring constant and x is the displacement from equilibrium.
• Total Energy (TE): The sum of kinetic and potential energy in a system. In SHM, when no energy is lost to friction or other external forces, the total energy remains constant.
• Displacement (x): The distance of an oscillating object from its equilibrium position, which can be positive or negative.
• Amplitude (x₀): The maximum displacement of an oscillating object from its equilibrium position.
• Angular Frequency (ω): A measure of how quickly an object oscillates, related to the frequency f and period T by ω = 2πf = 2π/T and ω = √(k/m)
• Spring Constant (k): A measure of the stiffness of a spring. The higher the spring constant, the more force required to stretch or compress the spring.
• Equilibrium Position: The position where there is no net force acting on the object, corresponding to zero potential energy and maximum kinetic energy.
• Oscillation: A single complete back-and-forth movement of an object around its equilibrium position.

 Apps

https://play.google.com/store/apps/details?id=com.ionicframework.shm181app497926

FAQ: Simple Harmonic Motion and Energy Transformation

1. What is Simple Harmonic Motion (SHM) in the context of a mass-spring system?
2. Simple Harmonic Motion (SHM) in a mass-spring system refers to the oscillatory motion of a mass attached to a spring, where the restoring force exerted by the spring is directly proportional to the displacement of the mass from its equilibrium position. This results in the mass moving back and forth in a repetitive pattern. The oscillation is characterized by a constant exchange between kinetic and potential energy.
3. How does energy transform during Simple Harmonic Motion?
4. In SHM, the total mechanical energy of the system (the sum of kinetic and potential energy) remains constant if no energy is lost. When the mass is at the equilibrium position (x=0), all the energy is in the form of kinetic energy (KE). As the mass moves away from equilibrium, KE is converted into potential energy (PE), stored in the stretched or compressed spring. At the maximum displacement (amplitude), all the energy is PE. The process then reverses, with PE converting back into KE as the mass moves back towards the equilibrium, continuously exchanging energy to maintain oscillation.
5. At what point in SHM is kinetic energy (KE) at its maximum and minimum?
6. Kinetic energy (KE) is at its maximum when the mass passes through the equilibrium position (x=0), where the velocity is greatest. KE is at its minimum (zero) at the points of maximum displacement (amplitude), where the mass momentarily stops before changing direction.
7. At what point in SHM is potential energy (PE) at its maximum and minimum?
8. Potential energy (PE) is at its maximum at the points of maximum displacement (amplitude), where the spring is either fully compressed or stretched and the mass has zero velocity. PE is at its minimum (zero) at the equilibrium position (x=0), where the spring is neither compressed nor stretched.
9. How is the total energy (TE) calculated in a mass-spring system undergoing SHM?
10. The total mechanical energy (TE) in SHM is the sum of kinetic energy (KE) and potential energy (PE). It can be expressed as TE = KE + PE. Given the formula for KE (1/2 * m * v^2) and PE (1/2 * k * x^2), and using relationships involving angular frequency (ω) and maximum displacement (x₀), the total energy can also be represented as TE = ½ * m * ω^2 * x₀^2, which is a constant value when no energy is lost.
11. What is the relationship between the velocity of the mass and its displacement in SHM?
12. The velocity (v) of the mass in SHM varies with its displacement (x). At the equilibrium position (x=0) velocity is maximum, and it decreases as the mass moves towards the points of maximum displacement (amplitude). At maximum displacement, the velocity is zero and changes direction. The mathematical relationship for velocity includes the square root of (x₀^2 - x^2), indicating that the velocity decreases as the displacement increases.
13. What are the formulas for calculating KE and PE in SHM?
14. The formulas for Kinetic Energy (KE) and Potential Energy (PE) in SHM are:

• KE = 1/2 * m * v^2 (where m is mass and v is velocity) or KE = 1/2 * m * ω^2 * (x₀^2 - x^2) (where ω is the angular frequency and x₀ is the amplitude)
• PE = 1/2 * k * x^2 (where k is the spring constant and x is the displacement) or PE = 1/2 * m * ω^2 * x^2

1. What does it mean that the total energy remains constant in SHM (assuming no energy is lost)?
2. If no energy is lost due to factors such as friction or air resistance during oscillation, the total mechanical energy of the system (the sum of the KE and PE) remains constant. This means that during the oscillations the energy of the system continuously transitions between KE and PE, but the overall amount of energy remains the same throughout. The energy doesn't diminish, it just changes form between kinetic and potential within the system.