About

Designed by Fu-Kwun Hwang http://www.phy.ntnu.edu.tw/ntnujava/ http://weelookang.blogspot.sg/2015/12/ejss-radioactive-decay-model.html  

Translations

Code	Language		Translator	Run

Credits

Fu-Kwun Hwang - Dept. of Physics, National Taiwan Normal Univ.; lookang; leongster

 

http://iwant2study.org/lookangejss/06QuantumPhysics_20nuclear/ejss_model_decaychangeNweedice/decaychangeNweedice_Simulation.xhtml

Briefing Document: Dice Throw JavaScript Model Simulation Applet HTML5

1. Overview

This document analyzes the provided material from Open Educational Resources / Open Source Physics @ Singapore, specifically focusing on the "Dice Throw JavaScript Model Simulation Applet HTML5" designed by Fu-Kwun Hwang and Leong Tze Kwang. The applet is a simulation designed to model radioactive decay using the analogy of dice throws. The goal is to provide an interactive and visual way for students to understand the probabilistic nature of radioactive decay. It is part of a larger collection of educational physics simulations and resources.

2. Key Themes and Concepts

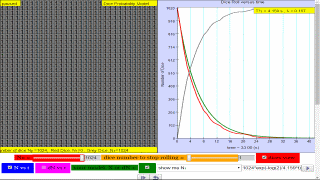
• Radioactive Decay Simulation: The core function of the applet is to simulate the process of radioactive decay. Instead of dealing directly with atoms, the applet uses the visual representation of boxes (representing nuclei) changing color (to red, representing decay) over time. This makes the abstract concept more accessible.
• Probability: A central idea is the probabilistic nature of decay, highlighting that each nucleus has an equal chance of decaying at any given time, but the precise moment of decay is random. The applet allows users to set the probability (p) for a nucleus to decay in each iteration.
• Mathematical Model: The applet is based on the mathematical model of radioactive decay. The document states:
• "Each nucleus has the same probability p (p<1) decayed into daughter product. It means that dN(t)/dt= -p*N(t) , where dN(t) is the number of nucleus decayed into daughter product at time t. The solution is N(t)=N0 e -pt = N 0 e -(ln2/T0.5)) t where N(0) is total number of nucleus at time t." This shows the connection between the simulation and the underlying theory. The equation connects the number of remaining nuclei N(t) at a given time t to the initial number of nuclei N0 through a decay constant related to the decay probability p or the half-life, T0.5.
• Visual Learning: The simulation uses color change (from initial color to red) to represent decayed nuclei, making it very visual. This can help different learning styles.
• Accessibility: This applet is designed to be accessible and usable on various platforms (Windows, MacOSX, Linux, ChromeBooks, Android/iOS devices).
• Open Educational Resource: The project is part of Open Educational Resources, emphasizing its role in free access to learning materials. It is provided under a Creative Commons Attribution-Share Alike 4.0 Singapore License, meaning it can be shared and adapted, provided the original source is credited.

3. Most Important Ideas/Facts

• Simulation as a Learning Tool: The primary function of the applet is as an interactive educational tool. The description explicitly mentions: "This applet let you set the probability for a nucleus to decay and watch how the number of decayed nuclei (color changed to RED) increased with time t."
• Probabilistic Decay: The concept that radioactive decay is a random process and described by a probability. It's not a deterministic "each will decay at x time," but instead each has a 'chance' of decaying within each iteration.
• Link to Mathematical Model: The simulation is grounded in a specific mathematical model that expresses the rate of change of radioactive nuclei: dN(t)/dt= -p*N(t). This reinforces the real-world physics the applet is simulating.
• Adaptability of Simulation: The applet offers a degree of flexibility, allowing users to adjust the decay probability, 'p', to visualize how that impacts the process.
• Easy JavaScript Simulation Framework: The applet is developed using the Easy JavaScript Simulation (EJS) framework, which is suitable for creating interactive simulations. This is also indicated by the tags "EasyJavaScriptSimulation" and the link to the blogpost: "http://weelookang.blogspot.sg/2015/12/ejss-radioactive-decay-model.html".
• Broader Context: The applet is one piece in a collection of over a thousand interactive simulations. This broad context includes topics from Newtonian mechanics to nuclear physics, all made with EJS, and showcases the depth of the project. The long list of topics, including "Tracker" simulations, reveals a broad use of simulation tools for physics education.

4. Key Quotes

• "Each nucleus has the same probability p (p<1) decayed into daughter product." (This emphasizes the probabilistic nature of decay)
• "This applet let you set the probability for a nucleus to decay and watch how the number of decayed nuclei (color changed to RED) increased with time t." (This highlights the interactive use of the simulation).
• "The solution is N(t)=N0 e -pt = N 0 e -(ln2/T0.5)) t" (This specifies the underlying mathematical formula used in the simulation).

5. Target Audience and Usage

• The tags associated with this particular applet ("Secondary", "Nuclear", "Junior College") show the target audience are likely high school students and beyond. The accessibility across platforms would suggest a broad implementation in classrooms.
• The simulation is likely intended for use in a classroom or self-study setting for learning about radioactive decay. The 'hands-on' nature of a simulation could make it more effective than purely theoretical explanations.

6. Further Resources

• The document also provides links to the original Java version of the simulation, a related blog post, and another similar Java version which all show the development of the current version of the applet.
• http://weelookang.blogspot.sg/2015/12/ejss-radioactive-decay-model.html
• http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=194.0
• http://www.opensourcephysics.org/items/detail.cfm?ID=10576

7. Conclusion

The "Dice Throw JavaScript Model Simulation Applet HTML5" is a well-designed, educational simulation tool that uses a visual representation to aid in understanding the probabilistic nature of radioactive decay. The applet's accessibility and connection to the underlying mathematical model make it an effective learning resource within the larger context of Open Educational Resources / Open Source Physics @ Singapore. The inclusion of the other resources highlights the depth of the educational resources available.

 

Dice Throw JavaScript Model Simulation Study Guide

Quiz

1. What does each box in the simulation represent? Each box in the simulation represents a radioactive nucleus that may decay over time. The simulation uses color changes to visually represent the decay of a nucleus.
2. What happens to the color of a box when its corresponding nucleus decays? When a nucleus decays, its corresponding box in the simulation changes color to red, visually indicating that the nucleus has transitioned into a daughter product.
3. What is the significance of the probability "p" in the context of the simulation? The probability "p" represents the likelihood that any given radioactive nucleus will decay within a specific timeframe. This value determines how quickly the decay process happens in the simulation.
4. How does the simulation relate the concept of probability to radioactive decay? The simulation shows how each nucleus has an independent probability of decay. This means that a particular nucleus will decay based on its own chance, and not necessarily due to the decay of a neighboring nucleus.
5. What is the purpose of the formula dN(t)/dt = -p*N(t)? The formula expresses the rate at which the number of undecayed nuclei changes over time. It mathematically represents that the rate of decay is proportional to the number of remaining nuclei.
6. What is the meaning of "N0" in the formula N(t) = N0e^(-pt)? "N0" represents the initial number of radioactive nuclei present at the beginning of the simulation, at time t=0.
7. What is the significance of T0.5 in the formula N(t) = N0e^(-(ln2/T0.5)t)? T0.5 represents the half-life of the radioactive material, which is the time it takes for half of the initial radioactive nuclei to decay. It is a key property of radioactive substances.
8. What is the benefit of using a JavaScript model for this simulation? Using a JavaScript model makes the simulation accessible on various platforms, including computers and mobile devices, without the need for special software. This provides a wide audience the opportunity to explore radioactive decay.
9. How can a user interact with the simulation to observe the effects of changing the decay probability? The user can interact with the simulation to set the probability for a nucleus to decay and then watch how the number of decayed nuclei increased with time t.
10. What real-world phenomena does this simulation aim to model? This simulation aims to model the process of radioactive decay, a real-world phenomenon where unstable atomic nuclei spontaneously transform into more stable forms.

Answer Key

1. Each box in the simulation represents a radioactive nucleus that may decay over time. The simulation uses color changes to visually represent the decay of a nucleus.
2. When a nucleus decays, its corresponding box in the simulation changes color to red, visually indicating that the nucleus has transitioned into a daughter product.
3. The probability "p" represents the likelihood that any given radioactive nucleus will decay within a specific timeframe. This value determines how quickly the decay process happens in the simulation.
4. The simulation shows how each nucleus has an independent probability of decay. This means that a particular nucleus will decay based on its own chance, and not necessarily due to the decay of a neighboring nucleus.
5. The formula expresses the rate at which the number of undecayed nuclei changes over time. It mathematically represents that the rate of decay is proportional to the number of remaining nuclei.
6. "N0" represents the initial number of radioactive nuclei present at the beginning of the simulation, at time t=0.
7. T0.5 represents the half-life of the radioactive material, which is the time it takes for half of the initial radioactive nuclei to decay. It is a key property of radioactive substances.
8. Using a JavaScript model makes the simulation accessible on various platforms, including computers and mobile devices, without the need for special software. This provides a wide audience the opportunity to explore radioactive decay.
9. The user can interact with the simulation to set the probability for a nucleus to decay and then watch how the number of decayed nuclei increased with time t.
10. This simulation aims to model the process of radioactive decay, a real-world phenomenon where unstable atomic nuclei spontaneously transform into more stable forms.

Essay Questions

1. Discuss how the Dice Throw JavaScript Model Simulation illustrates the concept of exponential decay. How does the simulation's visual representation of decay relate to the mathematical formula N(t) = N0e^(-pt)?
2. Analyze the role of probability in radioactive decay and how the simulation demonstrates the probabilistic nature of this phenomenon. In what ways does the simulation clarify the distinction between individual nucleus decay and the overall decay rate?
3. Compare and contrast the concepts of probability of decay and half-life (T0.5) as they appear in the simulation and in the associated formulas. Explain why it is essential to understand both concepts in the context of radioactive materials.
4. Critically evaluate the use of a simulation model like this for educational purposes. Discuss its advantages and limitations compared to learning through textbooks and traditional classroom instruction. How could the simulation be used to enhance learning about radioactive decay in different learning contexts?
5. Explore the broader applications of radioactive decay principles, making connections to other areas of physics or real-world uses. How can a strong understanding of concepts modeled by the simulation inform understanding or solutions related to topics such as carbon dating, nuclear power, or medical treatments?

Glossary

Radioactive Nucleus: An unstable atom that emits radiation as it decays to become more stable.

Daughter Product: The resulting nucleus after a radioactive nucleus undergoes decay.

Probability (p): The likelihood that a given event will occur, in this case, the decay of a single nucleus. This value is between 0 and 1.

Exponential Decay: A process where a quantity decreases at a rate proportional to its current value, often characterized by a decreasing curve as time increases.

dN(t)/dt: The rate of change in the number of radioactive nuclei with respect to time.

N(t): The number of radioactive nuclei at a given time "t".

N0: The initial number of radioactive nuclei at the beginning of the process, when t=0.

Half-life (T0.5): The time it takes for half of the radioactive nuclei in a sample to decay.

JavaScript Simulation: A model created using the JavaScript programming language, allowing for interactive visual representations.

Theory

Assume the number of radioactive nucleus is N(t) --- not yet decayed into daughter product.
Each nucleus has the same probability p (p<1) decayed into daughter product.
It means that dN(t)/dt= -p*N(t) , where dN(t) is the number of nucleus decayed into daughter product at time t.
The solution is N(t)=N₀ e ^-pt = N0 e -(ln2/T_0.5)) t where N(0) is total number of nucleus at time t.

Each box represent a nucleus.
This applet let you set the probability for a nucleus to decay and watch how the number of decayed nuclei (color changed to RED)  increased with time t.

 

YouTube

 

Other Resources

1. http://weelookang.blogspot.sg/2015/12/ejss-radioactive-decay-model.html lookang's blogpost about this JavaScript version
2. http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=194.0 by Fu-Kwun Hwang original Java version
3. http://www.opensourcephysics.org/items/detail.cfm?ID=10576 by Wolfgang Christian similar Java version

 

Frequently Asked Questions About the Dice Throw Radioactive Decay Simulation

1. What does this simulation model demonstrate? This simulation models radioactive decay, specifically focusing on how the number of radioactive nuclei decreases over time as they decay into daughter products. Each box in the simulation represents a radioactive nucleus, and the applet allows users to visualize the process by changing the color of decayed nuclei (to red). It illustrates the concept that each nucleus has a certain probability of decaying over a period.
2. How is radioactive decay probability represented in the model? The simulation allows you to set a probability ('p') for each nucleus to decay. This value represents the likelihood of a single nucleus transforming into a daughter product in any given time step. It is a probabilistic model, not deterministic, which means each nucleus has a chance to decay, but it is not guaranteed to occur at any specific moment.
3. What is the underlying mathematical principle of the simulation? The simulation is based on the differential equation dN(t)/dt = -p*N(t), where N(t) is the number of radioactive nuclei at time t, and p is the probability of decay. This leads to the solution N(t) = N₀ * e^(-pt), indicating an exponential decay of the number of radioactive nuclei over time. This equation is further expressed as N(t) = N ₀ * e -((ln2/T₀.₅)t) when half life is considered.
4. What is the role of the half-life in the simulation? The half-life (T₀.₅) is implicitly used in the equation, where the decay constant ('p') can be expressed as ln(2)/T₀.₅. This implies that a higher probability of decay corresponds to a shorter half-life and a faster decay of the overall population of radioactive nuclei.
5. What are some practical uses of this simulation? This simulation is particularly useful for educational purposes, primarily for secondary and junior college levels. It enables students to visually understand the abstract concepts of radioactive decay, exponential decay, and half-life. It is an accessible tool for demonstrating how decay processes happen at a microscopic level, bridging the gap between mathematical equations and actual physical processes.
6. Can I use this simulation on different devices? Yes, the simulation is designed to run on a variety of devices including desktops, laptops, tablets, and smartphones (Android/iOS). This accessibility makes it useful for diverse learning environments, ensuring students can engage with the simulation regardless of the technology available.
7. Who created this simulation, and where can I find more resources? This JavaScript model was created by Fu-Kwun Hwang and Leong Tze Kwang. More resources and background information can be found at the following links:

• Fu-Kwun Hwang's website: http://www.phy.ntnu.edu.tw/ntnujava/
• Lookang's blogpost about the Javascript version: http://weelookang.blogspot.sg/2015/12/ejss-radioactive-decay-model.html
• Fu-Kwun Hwang's original Java version: http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=194.0
• A similar Java version by Wolfgang Christian: http://www.opensourcephysics.org/items/detail.cfm?ID=10576

1. What kind of license is this simulation released under? The educational content including this simulation is released under a Creative Commons Attribution-Share Alike 4.0 Singapore License. Commercial use of the underlying EasyJavaScriptSimulations library requires a separate license agreement and contact with This email address is being protected from spambots. You need JavaScript enabled to view it..