About

Topics

Transverse and longitudinal waves

Description

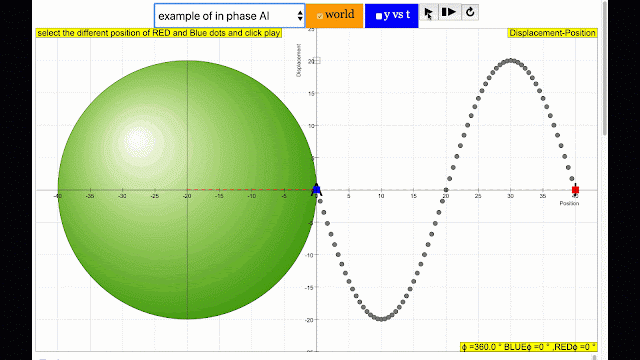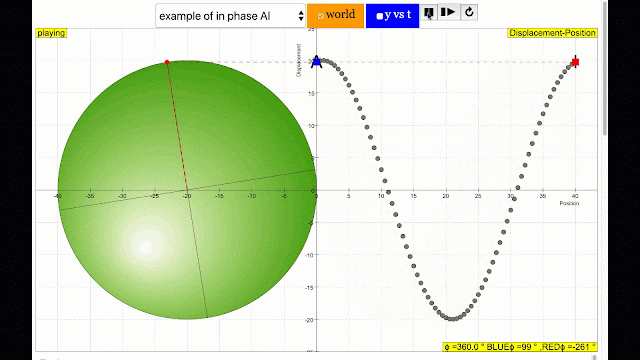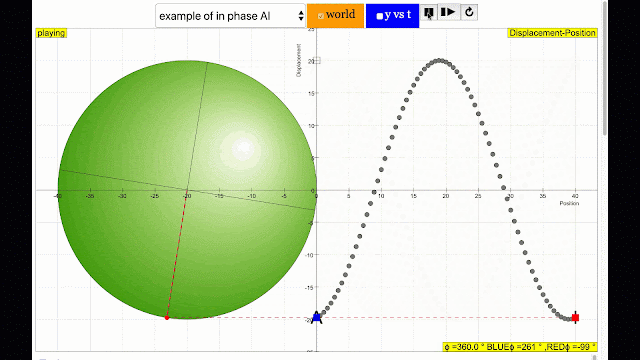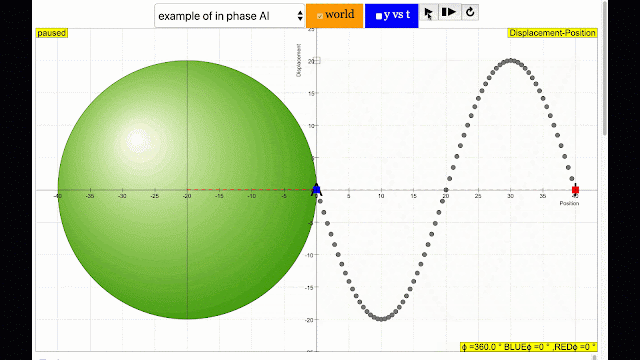
In this Transverse wave model, the simulation shows the phase difference commonly associated in wave motion in terms of angle differences between the 2 points travelling in a circular motion.

Play with the Model. Test what you've learned by exploring the  phase difference, amplitudes, wavelengths, periods, frequencies and  wave velocities.

Sample Learning Goals

(a) show an understanding and use the terms displacement, amplitude, phase difference, period,
frequency, wavelength and speed
(f) analyse and interpret graphical representations of transverse and longitudinal waves

Activities

1. By changing i and j sliders, the different positions of a wave can be simulated.
2. Determine the phase difference between the BLUE and RED point using ϕ/(2π) = t/T or otherwise. 
3. Use the simulation to check your calculation. 
4. The slider T changes the period of the wave motion, by means of evidences from the simulation or otherwise, determine the period 
5. The slider A changes the amplitude of the wave motion, by means of evidences from the simulation or otherwise, determine the amplitude
6. the guide allows the visualization of the front view of the point BLUE and RED.

Version:

1. http://weelookang.blogspot.sg/2015/07/ejss-transverse-wave-model.html
2. http://iwant2study.org/lookangejss/04waves_12generalwaves/ejs/ejs_model_waves_leetl_wee_v6.jar

http://weelookang.blogspot.sg/2015/07/ejss-transverse-wave-model.html

 

Translations

Code	Language		Translator	Run

Credits

Lee Tat Leong; Wee Loo Kang

Briefing Document: ⚛️Transverse Phase Difference Wave Simulation

1. Overview

This document analyzes a resource from Open Educational Resources / Open Source Physics @ Singapore, specifically a JavaScript HTML5 applet simulation model focused on transverse waves and phase difference. This simulation is designed as an interactive tool for learning and exploring the concepts related to wave motion. The simulation is embeddable and compatible with various devices (desktops, laptops, tablets, smartphones).

2. Core Concepts and Themes

The primary focus of the simulation is understanding phase difference in transverse waves. It uses the visual aid of circular motion to represent wave motion and emphasizes that phase is the position of a point in time on a waveform cycle. The core concepts and themes include:

• Transverse Waves: The model specifically simulates transverse waves, where the oscillations are perpendicular to the direction of wave propagation.
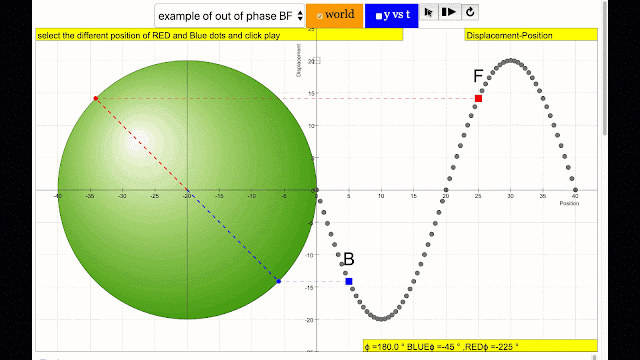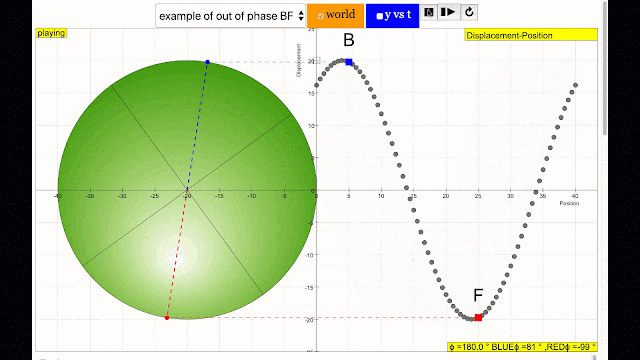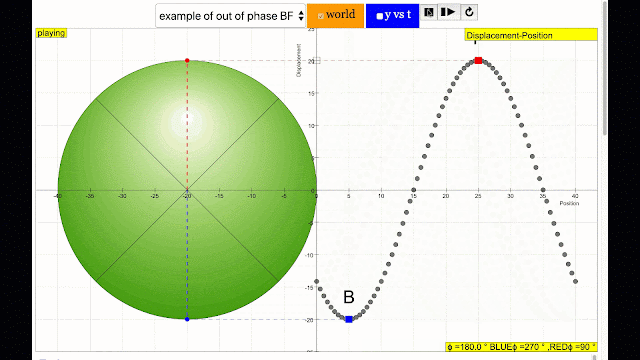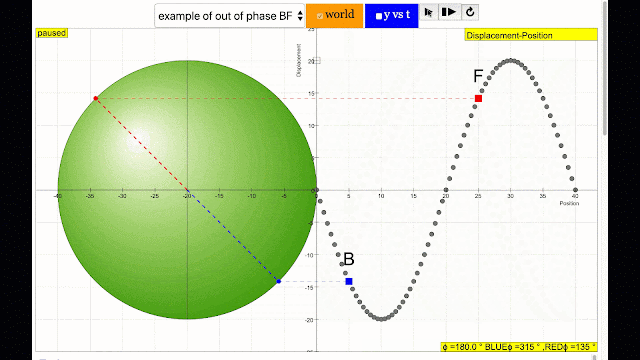
• Phase Difference: The simulation allows users to observe and manipulate the phase difference between two points on a wave (represented by blue and red points). This difference is quantified as an angle, where a complete cycle is 360 degrees. The model introduces the terms "in phase" (0 degree difference) and "antiphase" (180 degree difference).
• Wave Properties: Users can explore key wave properties such as:
• Displacement: The distance of a particle from its equilibrium position.
• Amplitude: The maximum displacement of a wave.
• Wavelength: The distance between two successive points in phase.
• Period (T): The time for one complete oscillation.
• Frequency (f): The number of oscillations per unit of time.
• Wave Velocity: The speed at which the wave propagates.
• Superposition: While not explicitly stated, the manipulation of phase difference implicitly allows users to grasp the idea that wave interference results from the combination of waves.

3. Key Ideas and Facts

• Interactive Learning: The simulation is designed for hands-on exploration. Users can change parameters using sliders, allowing them to investigate the effects of different variables on wave motion.
• Circular Motion Analogy: The simulation uses circular motion to illustrate the phase relationship between different points in a transverse wave. This is a common and effective method for visualizing the concept.
• Mathematical Connections: The simulation implicitly reinforces the mathematical relationship between phase difference, time (t), and period (T), using the formula "ϕ/(2 π ) = t/T" to demonstrate how phase differences can be calculated.
• Visualization Aids: The inclusion of a 'guide' allows users to see a front view of the blue and red points' motion, further helping visualize the phase difference.
• Specific Phase Relationships: The text emphasizes that:
• "phase difference equal to zero also called in phase" and provides examples.
• "phase difference equal to 180 degrees also called antiphase" and provides several examples of this relationship. It highlights that "out of phase" is not specific enough and that this term could mean any value from 1 to 179 degrees.
• Practical Application: The simulation provides learning activities that encourage users to verify calculated phase differences, periods, and amplitudes.

4. Important Quotes

• "In this Transverse wave model, the simulation shows the phase difference commonly associated in wave motion in terms of angle differences between the 2 points travelling in a circular motion."
• "Play with the Model. Test what you've learned by exploring the phase difference, amplitudes, wavelengths, periods, frequencies and wave velocities."
• "Phase is the position of a point in time (an instant) on a waveform cycle. A complete cycle is defined as the interval required for the waveform to return to its arbitrary initial value."
• "phase difference equal to zero also called in phase. notice point A and I are moving up and down the wave where their projected position on the circle form 0 degree difference, thus called in phase."
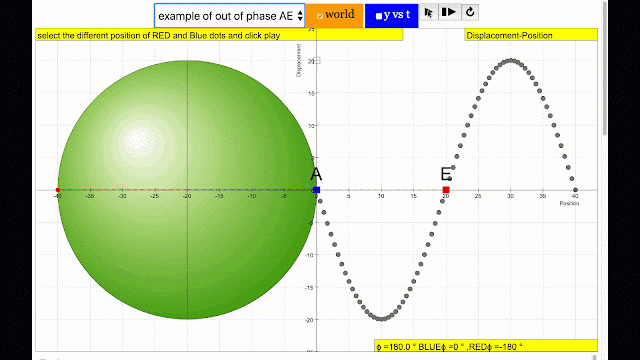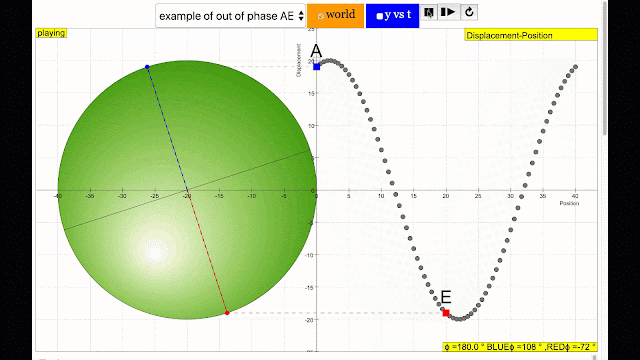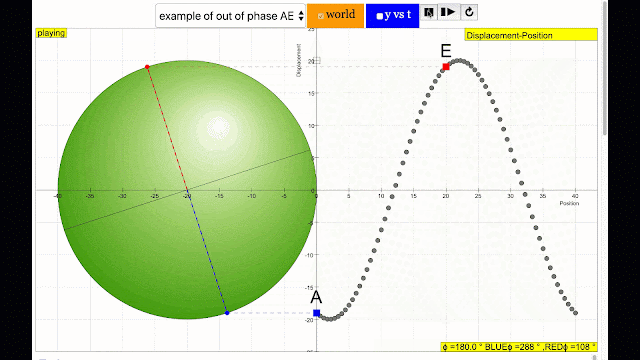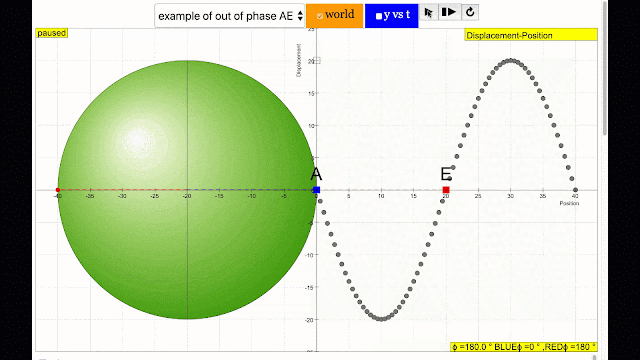
• "phase difference equal to 180 degrees also called antiphase. notice point A and E are moving up and down the wave where their projected position on the circle form 180 degree difference, thus called antiphase. Note that out of phase is implied but insufficient to describe the relation as out of phase can also mean angles from 1 to 179 degrees."

5. Learning Goals

The simulation is intended to meet the following learning goals:

• Understanding and using terms related to waves such as displacement, amplitude, phase difference, period, frequency, wavelength, and speed.
• Analyzing and interpreting graphical representations of transverse and longitudinal waves.

6. Activities

The simulation encourages interactive learning through activities:

• Simulating different wave positions by changing "i" and "j" sliders.
• Calculating the phase difference using the formula ϕ/(2 π ) = t/T and comparing with the simulation.
• Determining the wave period through the simulation and slider control of T.
• Determining the wave amplitude through the simulation and slider control of A.
• Visualizing the motion of the wave's points from the front.

7. Technical Aspects

• The model is a JavaScript HTML5 applet, implying cross-platform compatibility across browsers and operating systems.
• It utilizes EasyJavaScriptSimulation (EJS) framework, a common tool for educational simulations.
• The page provides links to embed the model, view its source code and introduction page.

8. Connections to Other Resources

The webpage links to numerous other simulation models, focusing on areas such as oscillations, simple harmonic motion, electromagnetism, optics, and more, demonstrating the breadth of educational resources available on this platform. These resources are accessible under a Creative Commons license and encourages open educational resource creation.

9. Conclusion

This simulation is a valuable interactive tool for learning about transverse waves and phase differences. Its emphasis on visual representation, interactive manipulation, and concrete learning activities can effectively help students understand abstract wave concepts. The use of EJS technology ensures accessibility and adaptability for educators and learners alike.

 

Transverse Wave Phase Difference Study Guide

Quiz

Instructions: Answer the following questions in 2-3 sentences each.

1. What is meant by the term "phase difference" in the context of wave motion?
2. Explain the difference between "in phase" and "antiphase" as they relate to waves.
3. How is the phase difference between two points on a wave represented using angles?
4. According to the source, what is a complete cycle of a waveform?
5. What is the significance of the sliders 'i' and 'j' in the simulation model?
6. How can the simulation be used to determine the period of a wave?
7. How can the simulation be used to determine the amplitude of a wave?
8. What is the relationship between phase difference and the relative movement of points on a wave?
9. How can the equation ϕ/(2π) = t/T be used in relation to phase difference?
10. What are some of the learning goals for using this simulation?

Quiz Answer Key

1. Phase difference refers to the difference in the position of two points on a wave cycle, often expressed as an angle. It indicates how far apart two points are in their oscillatory motion within the wave.
2. "In phase" means the phase difference between two points is zero degrees, meaning they move in synchrony. "Antiphase" means they have a phase difference of 180 degrees, thus moving in opposite directions.
3. Phase difference is expressed in angles, with a complete cycle being 360 degrees. A phase difference of 90 degrees means one point is a quarter of a cycle ahead or behind another.
4. A complete cycle of a waveform is the interval required for the waveform to return to its arbitrary initial value. This is equivalent to 360 degrees of phase.
5. The 'i' and 'j' sliders in the simulation model allow the user to change the position of two points on the wave, which are used to demonstrate the phase difference between points.
6. By observing the movement of a point on the wave in the simulation and using the time slider 'T' to adjust the period, you can determine the amount of time it takes to complete a full cycle of the wave.
7. By observing the vertical displacement of a point on the wave in the simulation and using the amplitude slider 'A,' you can determine the maximum displacement from the equilibrium position.
8. A phase difference of 0° indicates points move in the same direction simultaneously, while 180° indicates they move in opposite directions. Any other angle difference indicates they move out of sync at a specific difference in position of the wave cycle.
9. The equation ϕ/(2π) = t/T allows for the calculation of the phase difference (ϕ) using the time difference between the two points (t) and the period of the wave (T).
10. Some of the learning goals include understanding the terms displacement, amplitude, phase difference, period, frequency, wavelength and speed, as well as analyzing graphical representations of transverse and longitudinal waves.

Essay Questions

Instructions: Answer the following questions in well-structured essays.

1. Discuss the significance of phase difference in understanding wave behavior, providing examples from the simulation or otherwise to support your arguments.
2. Explain how changing parameters like period and amplitude affects the visual representation of a transverse wave, and how the simulation helps demonstrate these relationships.
3. Analyze the relationship between phase difference, time difference, and period, using the equation ϕ/(2π) = t/T.
4. Compare and contrast the concepts of "in phase" and "antiphase," and explain why the source distinguishes "out of phase" as insufficient to describe the relation fully.
5. How can simulation models like the one described in the source aid in student learning about wave properties and characteristics? Use specific examples from the text and your own understanding of these concepts.

Glossary of Key Terms

• Amplitude: The maximum displacement of a wave from its equilibrium position. It represents the height or intensity of the wave.
• Antiphase: A phase difference of 180 degrees between two points on a wave, where their motions are in opposite directions.
• Displacement: The distance of a point on the wave from its equilibrium position at a given time.
• Frequency: The number of complete cycles of a wave that pass a given point per unit time, typically measured in Hertz (Hz).
• In Phase: A phase difference of zero degrees between two points on a wave, meaning they move in synchrony.
• Longitudinal Wave: A type of wave where the oscillations of the particles are parallel to the direction of wave propagation (e.g., sound waves).
• Out of Phase: A general term indicating that two points on a wave are not synchronized; however, this term can be insufficient because it doesn't specify the precise angle of phase difference
• Period: The time taken for one complete cycle of a wave to occur, typically measured in seconds.
• Phase Difference: The difference in the phase of two points on a wave, expressed as an angle, typically in degrees.
• Transverse Wave: A type of wave where the oscillations of the particles are perpendicular to the direction of wave propagation (e.g., light waves).
• Wave Velocity: The speed at which a wave propagates, often related to the frequency and wavelength.
• Wavelength: The distance between two successive crests or troughs of a wave.

Description

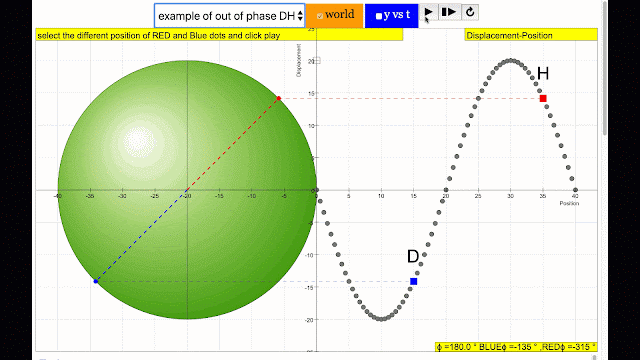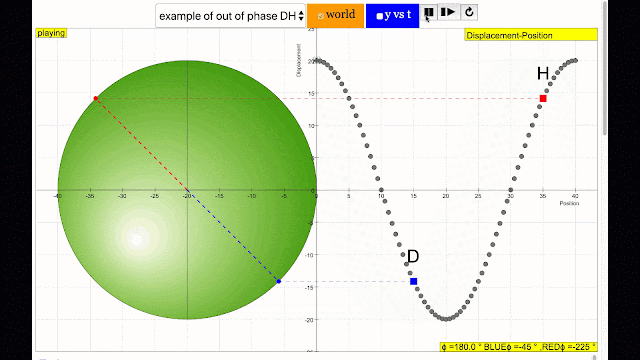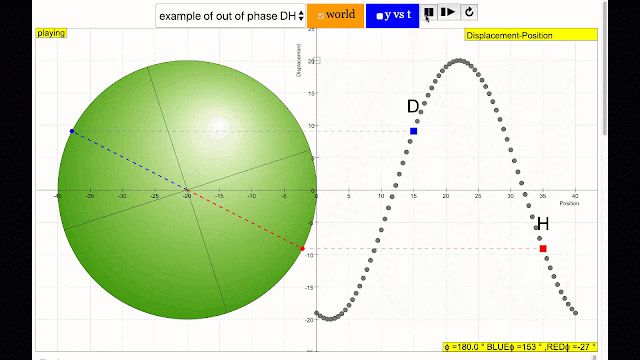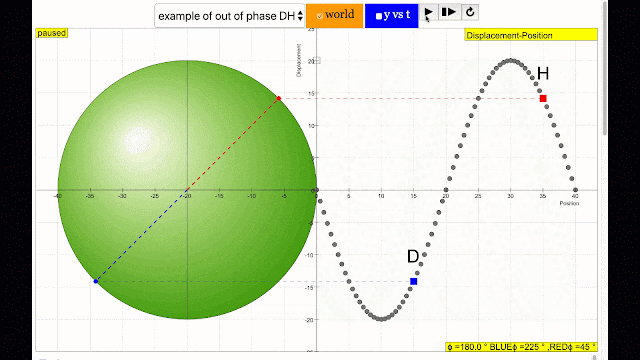
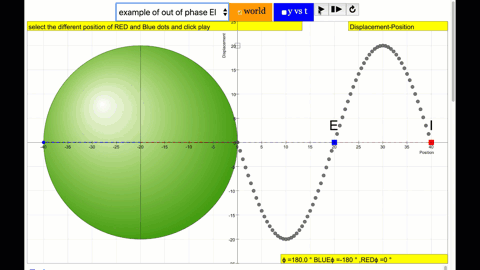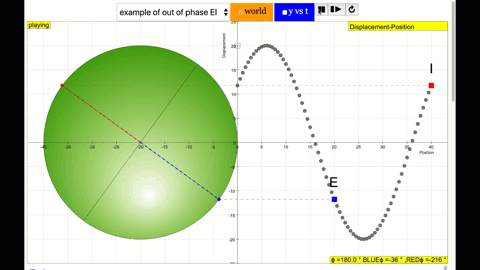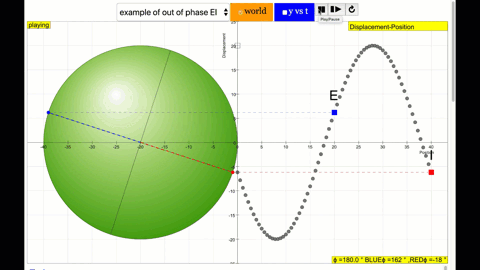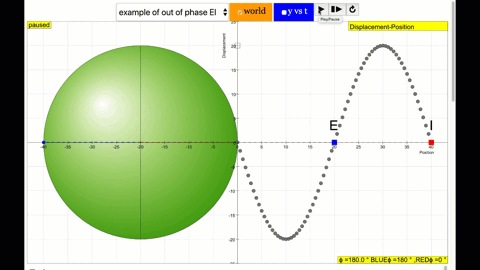
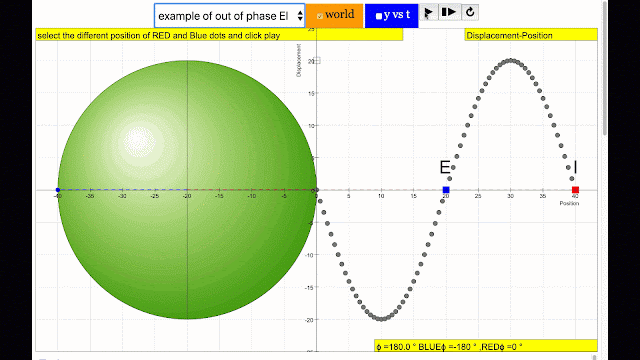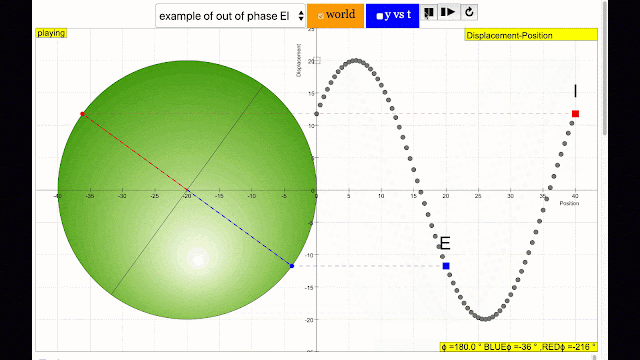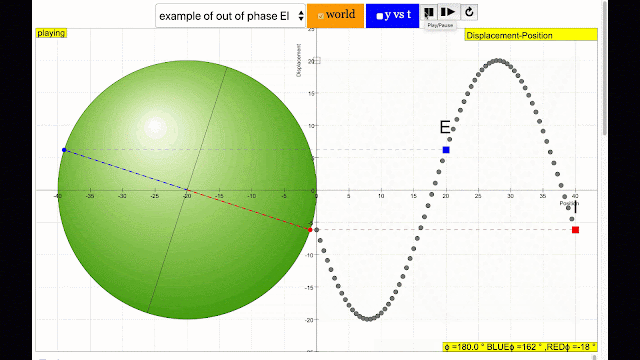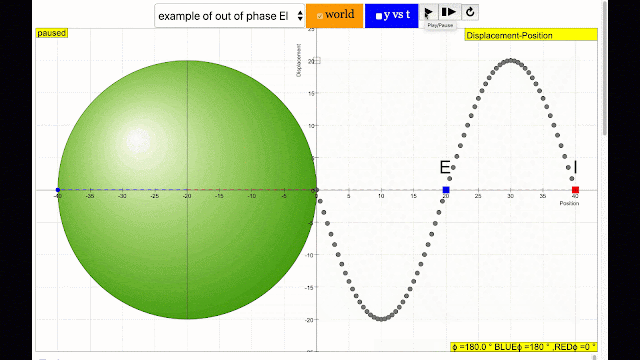
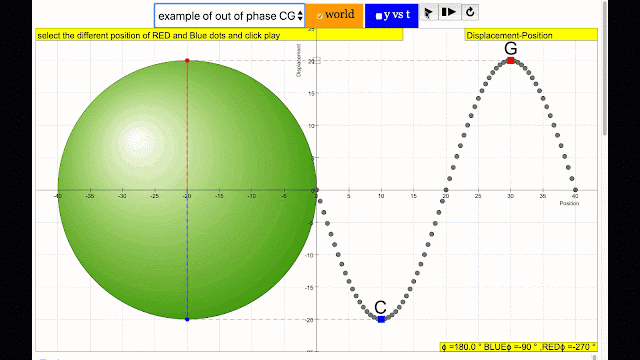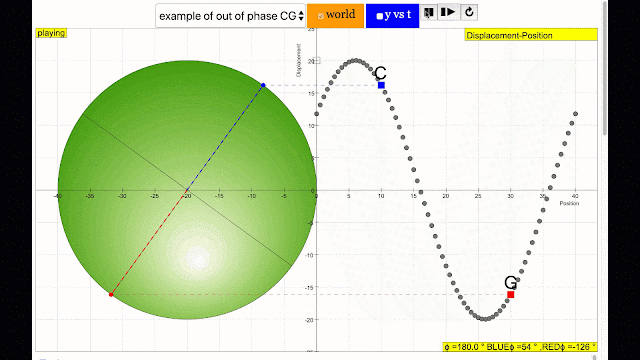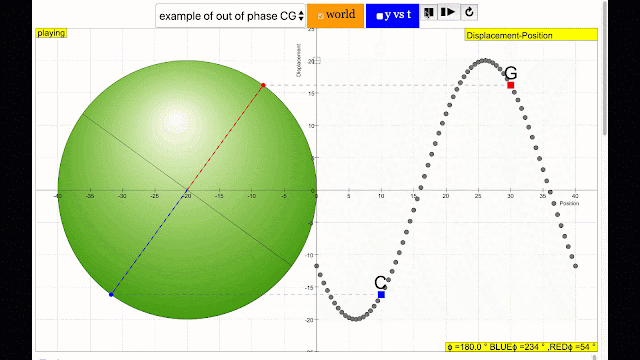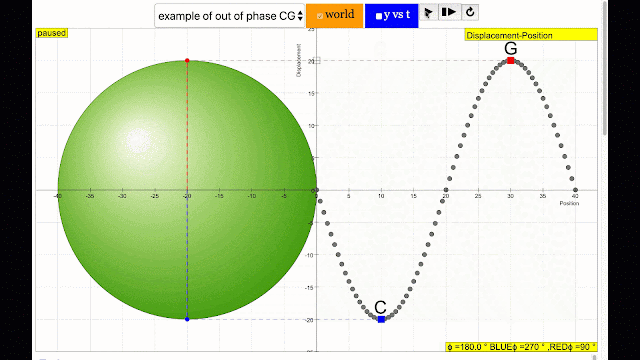
Phase is the position of a point in time (an instant) on a waveform cycle. A complete cycle is defined as the interval required for the waveform to return to its arbitrary initial value. The graph to the right shows how one cycle constitutes 360° of phase.

phase difference equal to zero also called in phase. notice point A and I are moving up and down the wave where their projected position on the circle form 0 degree difference, thus called in phase.

phase difference equal to 180 degrees also called antiphase. notice point A and E are moving up and down the wave where their projected position on the circle form 180 degree difference, thus called antiphase. Note that out of phase is implied but insufficient to describe the relation as out of phase can also mean angles from 1 to 179 degrees.

 

phase difference equal to 180 degrees also called antiphase. notice point B and F are moving up and down the wave where their projected position on the circle form 180 degree difference, thus called antiphase. Note that out of phase is implied but insufficient to describe the relation as out of phase can also mean angles from 1 to 179 degrees.

 

phase difference equal to 180 degrees also called antiphase. notice point D and H are moving up and down the wave where their projected position on the circle form 180 degree difference, thus called antiphase. Note that out of phase is implied but insufficient to describe the relation as out of phase can also mean angles from 1 to 179 degrees.

 

phase difference equal to 180 degrees also called antiphase. notice point E and I are moving up and down the wave where their projected position on the circle form 180 degree difference, thus called antiphase. Note that out of phase is implied but insufficient to describe the relation as out of phase can also mean angles from 1 to 179 degrees.

 

phase difference equal to 180 degrees also called antiphase. notice point E and I are moving up and down the wave where their projected position on the circle form 180 degree difference, thus called antiphase. Note that out of phase is implied but insufficient to describe the relation as out of phase can also mean angles from 1 to 179 degrees.

 

phase difference equal to 180 degrees also called antiphase. notice point C and G are moving up and down the wave where their projected position on the circle form 180 degree difference, thus called antiphase. Note that out of phase is implied but insufficient to describe the relation as out of phase can also mean angles from 1 to 179 degrees.

Video

 

Versions

http://weelookang.blogspot.com/2019/01/transverse-phase-difference-wave.html 

Phase Difference

 

FAQ: Understanding Transverse Waves and Phase Difference

• What is a transverse wave, and how does the provided simulation model it? A transverse wave is a wave where the oscillations are perpendicular to the direction of the wave's travel. The simulation models this by showing two points (represented by blue and red) moving in circular paths. The vertical positions of these points correspond to the displacements of the wave at different locations. The simulation visualizes a wave travelling from left to right where the points on the wave move up and down, perpendicularly to the direction of wave propagation. This gives a visual representation of a transverse wave.
• What are the key parameters that can be explored using this simulation? The simulation allows for the exploration of several key wave parameters: phase difference, amplitudes, wavelengths, periods, frequencies, and wave velocities. Users can directly manipulate sliders to observe the effects of changing these values. This interactive aspect enhances understanding of how these parameters relate to wave motion.
• What is phase difference, and how is it represented in the simulation? Phase difference refers to the difference in the position of two points on a wave cycle, measured as an angle. In the simulation, the phase difference between the blue and red points is the angle difference between their positions on their respective circular paths. A full cycle of the wave corresponds to 360 degrees or 2π radians. The simulation highlights in-phase (0 degrees difference) and antiphase (180 degrees difference) scenarios by visualising the difference in the points' positions on the circular path. The positions of each point are then projected onto the wave to show how the phase difference affects their positions on the wave.
• How can I determine the phase difference between two points in the simulation? The phase difference (ϕ) can be determined using the formula: ϕ/(2π) = t/T, where 't' is the time difference between the two points’ positions in the wave cycle and 'T' is the period of the wave. The simulation allows users to manipulate sliders, see how 't' changes, and visually check their calculated phase difference, reinforcing the relationship between time, period, and phase difference. It allows users to observe the projected motion of the point in the circle along the wave to see the phase difference as the position of these points.
• What does it mean for two points on a wave to be "in phase" and "antiphase"? When two points on a wave are "in phase," they have a phase difference of 0 degrees (or multiples of 360 degrees). This means they are at the same position in their wave cycle; they move up and down together. Conversely, when points are "antiphase," they have a phase difference of 180 degrees (or odd multiples of 180 degrees). They are at opposite points in their wave cycle; while one moves upward, the other moves downward, and vice versa. This is clearly shown in the example provided with different points moving along the transverse wave and the relative positions of their phases in their respective circular paths.
• How can the simulation help in understanding the relationship between period and frequency? The period (T) of a wave is the time it takes for one complete cycle, while frequency (f) is the number of cycles per unit time. They are inversely related (f = 1/T). In the simulation, manipulating the period slider directly changes the wave’s speed and the pace at which the points on the wave go through their circular motion. By observing the simulation, students can see that a shorter period leads to a higher frequency and vice versa, enhancing their understanding of the concept.
• How can the amplitude of a wave be visualized and changed in the simulation? The amplitude is the maximum displacement of a wave from its equilibrium position. The simulation allows users to change the amplitude by using the slider labelled 'A'. Increasing the value of the slider will increase the radius of the circular motion of the blue and red points, which correspondingly increases the displacement of the points on the wave. This gives a clear visual and hands-on way to understand wave amplitude.
• What other educational resources or activities are related to this simulation? The provided context includes a rich list of other simulations and activities, covering various topics like ideal gas models, simple harmonic motion, energy transfers, collisions, vectors, and more. There are also resources on electromagnetism, optics, and even interactive games that help enhance understanding of different science and math topics. This suggests that this transverse wave simulation is part of a broader suite of educational tools.