About

1.2.12 Example 

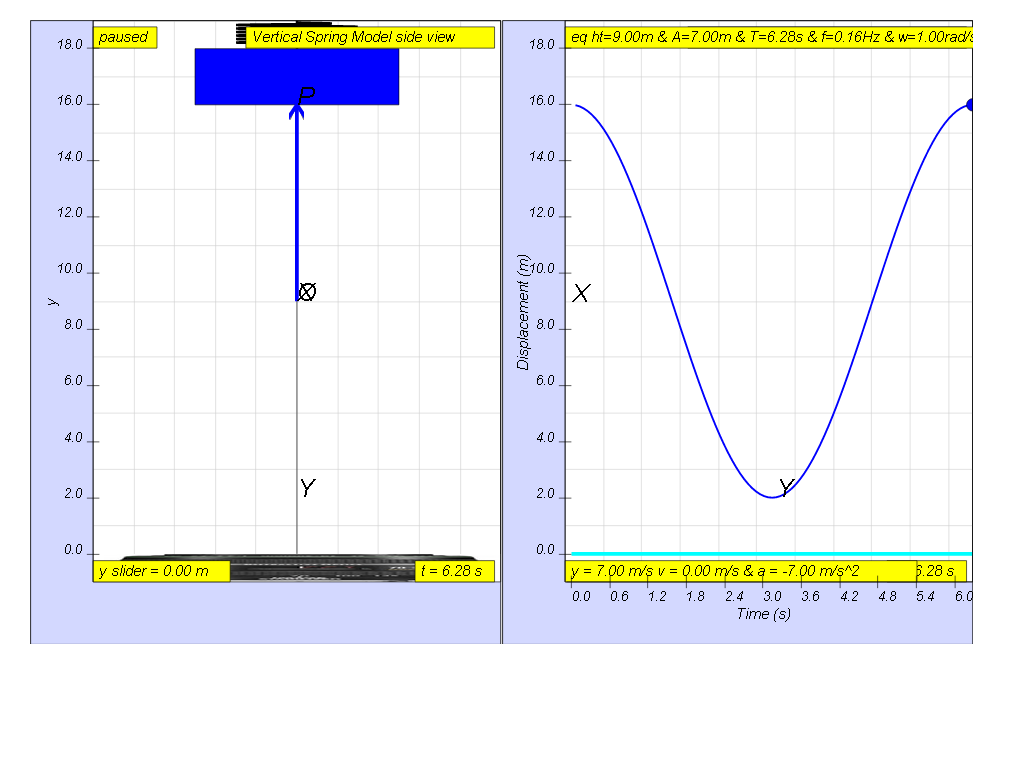
A mass undergoes an oscillation where the maximum/minimum amplitude is 16.0 m mark and 2.0 m mark on a rule respectively. It was found that the particle only takes 3.14 s to move from X = 16.0 m to Y = 2.0 m during the oscillations as shown. Determine the   
(a)     amplitude,      
(b)     period,     
(c)     frequency,      
(d)     angular frequency, of the oscillations.
[ 7.0 m, 6.28 s, 0.166 Hz, 1.00 rad/s ]

1.2.12.1Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/91

1.2.12.2 Inquiry

Q1: run model with different mass m and spring constant k to explore different amplitude x₀, period T, frequency f and angular frequency ω.
Q2: setup your own initial conditions and test your understanding of with is the physical meaning of amplitude x₀, period T, frequency f and angular frequency ω.

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM162/SHM162_Simulation.xhtml

Briefing Document: ⚛️Vertical Spring Mass Model Simulation

1. Introduction

This document summarizes the key aspects of an online interactive simulation of a vertical spring-mass model, accessible through a JavaScript HTML5 applet. This simulation is part of a larger collection of educational resources provided by "Open Educational Resources / Open Source Physics @ Singapore". The focus of the specific model is on exploring the concepts of simple harmonic motion (SHM).

2. Core Theme: Simple Harmonic Motion (SHM)

The primary theme is the exploration of Simple Harmonic Motion (SHM) through a vertical spring-mass system. The simulation allows users to manipulate parameters and observe the resulting oscillations. This is designed to help learners visualize and understand the key characteristics of SHM, like amplitude, period, frequency, and angular frequency. The provided text includes questions, which encourages active learning.

3. Simulation Details and Usage

• Accessibility: The simulation is designed to be accessible across multiple platforms, including:
• Android/iOS devices (handphones, tablets, iPads)
• Windows, MacOSX, Linux computers (laptops and desktops)
• ChromeBook laptops
• Embedding: The simulation can be embedded into webpages using an <iframe> tag.
• Interactive Nature: The simulation is intended to be interactive, allowing users to directly engage with the model through the web applet.
• Example Scenario: The provided text includes a worked example where a mass oscillates between 16.0 m and 2.0 m on a rule, taking 3.14 seconds to move between these positions. The solutions include:
• Amplitude: 7.0 m
• Period: 6.28 s
• Frequency: 0.166 Hz
• Angular Frequency: 1.00 rad/s
• Inquiry-Based Learning: The resource suggests two inquiry questions:
• Q1: "run model with different mass m and spring constant k to explore different amplitude x0, period T, frequency f and angular frequency ω." This prompts users to experiment with the simulation and understand the effect of changing variables.
• Q2: "setup your own initial conditions and test your understanding of with is the physical meaning of amplitude x0, period T, frequency f and angular frequency ω." This challenges users to apply their knowledge and test their understanding of the key terms in the context of SHM.

4. Key Concepts Covered

The simulation and the associated example focus on the following concepts: * Amplitude (x0): The maximum displacement of the mass from its equilibrium position. * Period (T): The time it takes for one complete oscillation. * Frequency (f): The number of oscillations per unit time (measured in Hertz). * Angular Frequency (ω): A measure of oscillation rate, related to frequency by ω = 2πf (measured in radians per second).

• Spring Constant (k): A measure of the stiffness of the spring
• Mass (m): The mass of the object attached to the spring

5. Related Resources

The provided text lists numerous related interactive simulations, covering a range of physics topics including:

• Other spring-mass systems (horizontal, varying parameters)
• Pendulums
• Gravity and potential energy
• Collisions
• Waves
• Optics
• Electromagnetism
• Various mathematics simulations and interactive games for different school levels.
• Use of webEJS editor, tutorials and workshops.
• The long list of projects highlights the resources are intended for classroom or self study at many levels.

These related resources suggest that the vertical spring-mass model is part of a comprehensive suite of interactive learning materials. This highlights the comprehensive nature of this OER offering.

6. Technological Foundation

• JavaScript and HTML5: The simulations are built using JavaScript and HTML5, making them widely accessible through web browsers.
• EasyJavaScriptSimulation (EJS): Many of the listed simulations (including this example) are built using EasyJavaScriptSimulation, a tool that enables the creation of interactive physics models.
• Open Source: The resources emphasize open educational resources and open source physics principles.

7. Licensing and Credits

• The content is licensed under a Creative Commons Attribution-Share Alike 4.0 Singapore License.
• Commercial use of the EasyJavaScriptSimulations library requires contacting This email address is being protected from spambots. You need JavaScript enabled to view it..

8. Conclusion

The provided source details a highly interactive vertical spring-mass model simulation that serves as an effective tool for learning about Simple Harmonic Motion (SHM). It emphasizes hands-on exploration with adjustable parameters, is easily accessible across many devices and platforms, and is integrated within a larger collection of educational tools for physics. The inclusion of inquiry-based learning questions and related resources makes it a valuable asset for educators and learners.

This concludes the briefing document. Let me know if you have other questions.

Vertical Spring-Mass Model Study Guide

Quiz

1. What are the maximum and minimum amplitude markers for the oscillating mass in the provided example?
2. How long does the particle take to move from its maximum position to its minimum position?
3. What is the period of the oscillation, according to the given example problem?
4. What is the definition of "frequency" in the context of oscillations?
5. What is meant by the term "angular frequency" and how is it related to frequency?
6. Briefly describe the relationship between mass and the period of oscillation in a spring-mass system.
7. How does the spring constant affect the period of oscillation in a spring-mass system?
8. What kind of technology is the simulation model based on?
9. What are some platforms this simulation can be run on?
10. Besides the spring mass model, name two other interactive models mentioned in this website.

Quiz Answer Key

1. The maximum amplitude marker is 16.0 m, and the minimum amplitude marker is 2.0 m.
2. The particle takes 3.14 seconds to move from its maximum position to its minimum position.
3. The period of the oscillation is 6.28 seconds.
4. Frequency is the number of complete oscillations (or cycles) that occur per unit of time, typically measured in Hertz (Hz).
5. Angular frequency (ω) measures the rate of change of the angle of the oscillation, and is related to frequency (f) by the equation ω = 2πf.
6. Generally, as the mass in a spring-mass system increases, the period of oscillation also increases.
7. A higher spring constant results in a shorter period of oscillation, meaning the spring will oscillate faster.
8. The simulation model is based on JavaScript HTML5 technology.
9. The simulation can be run on Android/iOS devices, including phones, tablets, and iPads; as well as Windows, macOS, Linux, and Chromebook laptops and desktops.
10. Two other interactive models are the "Pendulum JavaScript Model Simulation Applet HTML5" and "Newton Cradle JavaScript HTML5 Applet Simulation Model."

Essay Questions

1. Discuss how changing the mass and spring constant in the simulation affects the amplitude, period, and frequency of the oscillation. Be sure to reference the given example problem in your answer.
2. Explain the relationship between period, frequency, and angular frequency in the context of simple harmonic motion, and how these values are calculated for the given example problem.
3. Compare and contrast the concepts of amplitude, period, and frequency, and discuss their physical meaning in the context of oscillations.
4. How can this simulation be used to better understand the principles of simple harmonic motion, and what are the limitations of such a simulation?
5. Considering the wide variety of interactive models listed, discuss the potential for digital simulations as an educational tool.

Glossary

• Amplitude: The maximum displacement or distance moved by a point on a vibrating body or wave measured from its equilibrium position. In this example, the amplitude would be (16m-2m)/2=7m, and the center would be at 9m.
• Period (T): The time taken for one complete cycle or oscillation of a vibrating body, measured in seconds.
• Frequency (f): The number of complete cycles or oscillations per unit of time, measured in Hertz (Hz), which is cycles per second.
• Angular Frequency (ω): A measure of rotational rate, often used in oscillating systems. It is related to the frequency by the equation ω = 2πf, measured in radians per second (rad/s).
• Simple Harmonic Motion (SHM): A type of periodic motion where the restoring force is directly proportional to the displacement and acts in the direction opposite to that of displacement.
• Spring Constant (k): A measure of the stiffness of a spring, representing the force required to stretch or compress the spring a unit distance, typically measured in Newtons per meter (N/m).
• JavaScript HTML5: A combination of programming language and markup language used for creating interactive web content and applications.
• Open Educational Resources (OER): Freely accessible, openly licensed text, media, and other digital assets that are useful for teaching, learning, and assessment.
• Simulation: A computer-based representation or model of a real system or process used for study or experimentation.

 Apps

https://play.google.com/store/apps/details?id=com.ionicframework.shm161app280927&hl=en

FAQ

What is the focus of the provided simulation models?

The simulation models primarily focus on physics and mathematics concepts, particularly those related to Newtonian mechanics and oscillations. They utilize JavaScript and HTML5 to create interactive learning experiences, often visualizing concepts like simple harmonic motion, spring-mass systems, and gravitational fields. Many of these models also delve into topics like kinematics, vectors, optics, and even more advanced physics concepts such as wave-particle duality and special relativity. The simulations are designed to be accessible on a variety of platforms, including computers, tablets, and phones, making them suitable for diverse learning environments.

What is Easy JavaScript Simulation (EJS) and why is it significant?

Easy JavaScript Simulation (EJS) is an authoring toolkit used to create the interactive simulations showcased in the sources. It is significant because it allows educators and developers to build custom educational resources without extensive coding expertise. EJS facilitates the development of simulations that are not only interactive but also visually engaging, which promotes deeper understanding of complex scientific and mathematical principles. The use of EJS also fosters the creation of Open Educational Resources that can be shared and adapted freely. The presence of a webEJS editor further simplifies the simulation creation process, enabling more individuals to participate in resource development.

What specific topics within physics are covered by these simulations?

The simulations cover a broad spectrum of physics topics. These include: simple harmonic motion (SHM), spring-mass systems, pendulum motion, gravitational fields and potential, escape velocity, kinematics (motion, velocity, acceleration), vector addition and decomposition, collisions (elastic and inelastic), electromagnetic induction, and wave phenomena. Some models go beyond classical mechanics to explore topics in optics (diffraction, interference), quantum mechanics (hydrogen atom probability), and special relativity. Furthermore, some interactive simulations even venture into more real world systems like solar panels, metallic conductors, and even bus acceleration.

How can the simulations be used for educational purposes?

The simulations are designed to be highly interactive and inquiry-based. They allow students to manipulate variables such as mass, spring constants, initial conditions, and more to observe how these changes affect outcomes. Teachers can use these tools to facilitate both demonstration and experimentation, allowing students to explore physics principles at their own pace and engage more deeply with the concepts. There are suggestions of use in both primary and secondary schools, as well as higher educational institutions. They can also be used in a variety of learning environments, including classroom settings, individual study, and remote learning contexts, given their accessibility across different devices. The resources also promote critical and creative thinking.

Are there any examples of specific simulations mentioned in the sources?

Yes, there are numerous specific examples of simulations mentioned. These include models for: a vertical spring-mass system with a specific position (y=7m), a horizontal spring-mass system with variations in acceleration, velocity, and position, simulations of pendulum motion, various gravitational field simulations, collision carts, vector addition, projectile motion, light and shadow simulations, double slit diffraction models, and even simulations for the 555 timer integrated circuit and other electronic components. There is a diverse array of simulations, ranging from simple demonstrations to complex interactive experiments. Additionally, various games and quizzes based on these concepts have been created, showing how the simulations can be utilized to engage users in different ways.

How does the project encourage the sharing and development of educational resources?

The project heavily emphasizes the creation and sharing of open educational resources (OER). The simulations are often freely available online and are licensed under a Creative Commons Attribution-Share Alike license, which permits sharing and adaptation. This allows educators globally to freely access, use, and modify the resources to fit their needs. This collaborative approach is further amplified by workshops and project collaborations described in the sources. Furthermore, resources are shared on platforms such as the Student Learning Space (SLS).

What kind of additional applications and topics are presented outside of physics simulations?

Beyond physics, the simulations and resources delve into diverse educational topics like mathematics (e.g., vector addition, geometry, algebra, estimation games), English language skills (e.g., interactive vocabulary stories), chemistry (e.g., ionic bonding, electrolysis), geography (e.g., transit planners), design and technology (e.g., 555 timer circuits), music, and even economics. There are many projects described that incorporate games and challenges that would appeal to all learners, demonstrating the versatility of the EJS tool for diverse educational applications and demonstrating its adaptability in the learning process.

Are there any initiatives mentioned in the sources that support teachers and educators?

Yes, the sources mention several initiatives designed to support teachers and educators. These include workshops on how to use the webEJS editor, sharing sessions on in-house resource development, use of simulations for SLS, and providing customizable teacher versions of simulations and graphs. There are also numerous collaborative projects involving teachers in the development and implementation of these resources. This shows that the project recognizes the important role of educators and actively works to support them through access to training, support and collaborative communities that facilitate the creation and use of these simulations in the learning process.