About

1.1.3.2.3 Understanding Phase Difference through Uniform Circular Motion

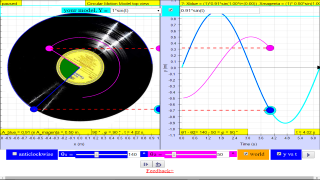
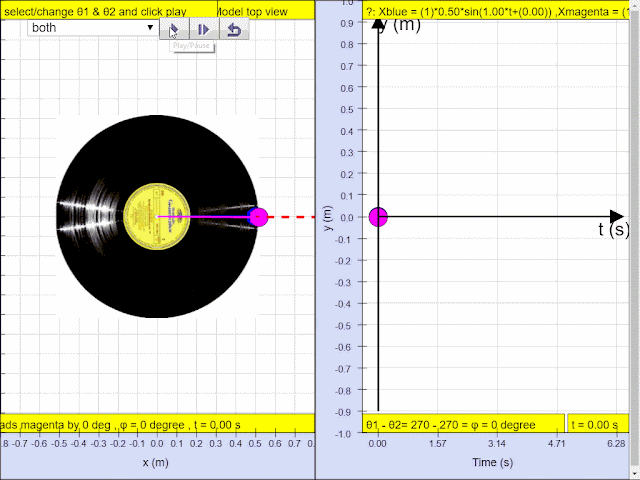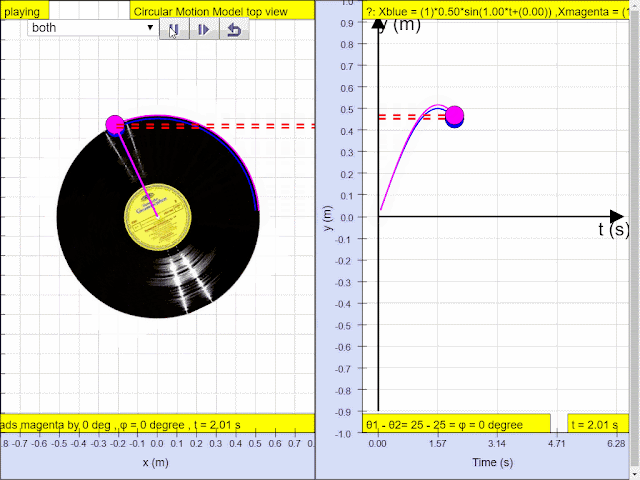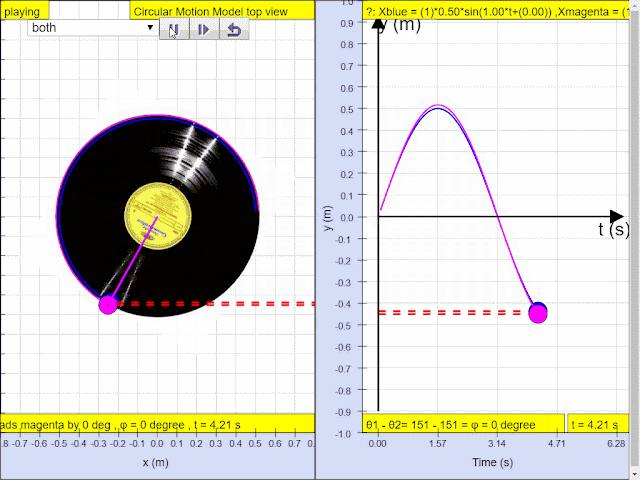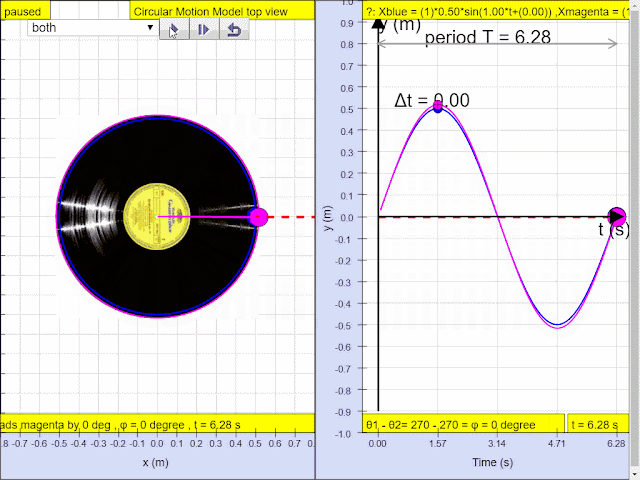
Simple harmonic motion can in some cases be considered to be the one-dimensional projection of uniform circular motion. If an object moves with angular speed ω around a circle of radius A centered at the origin of the x−y plane, then its motion along each coordinate is simple harmonic motion with amplitude A and angular frequency ω.

Q1: given that, a circular motion can be described by x = A cos(ω t)  and y A sin(ω t) what is the y-component model-equation that can describe the motion of a uniform circular motion?

A1: y = Asin (ωt)

Q2: When the x-component of the circular motion is modelled by x = A cos(ω t)  and y A sin(ω t) suggest an model-equation for y.

A2: y = Acos (ωt) for top position or y = - Acos (ωt) for bottom position

Q3: Explain why are the models for both x and y projection of a uniform circular motion, a simple harmonic motion?

A3: both x = A cos(ω t)  and y A sin(ω t) each follow the defining relationship for SHM as ordinary differential equations of   ${\displaystyle \frac{d^{2}x}{{dt}^2}=-{\omega }^{2}x}$ and  ${\displaystyle \frac{d^{2}y}{{dt}^2}=-{\omega }^{2}y}$ respectively.

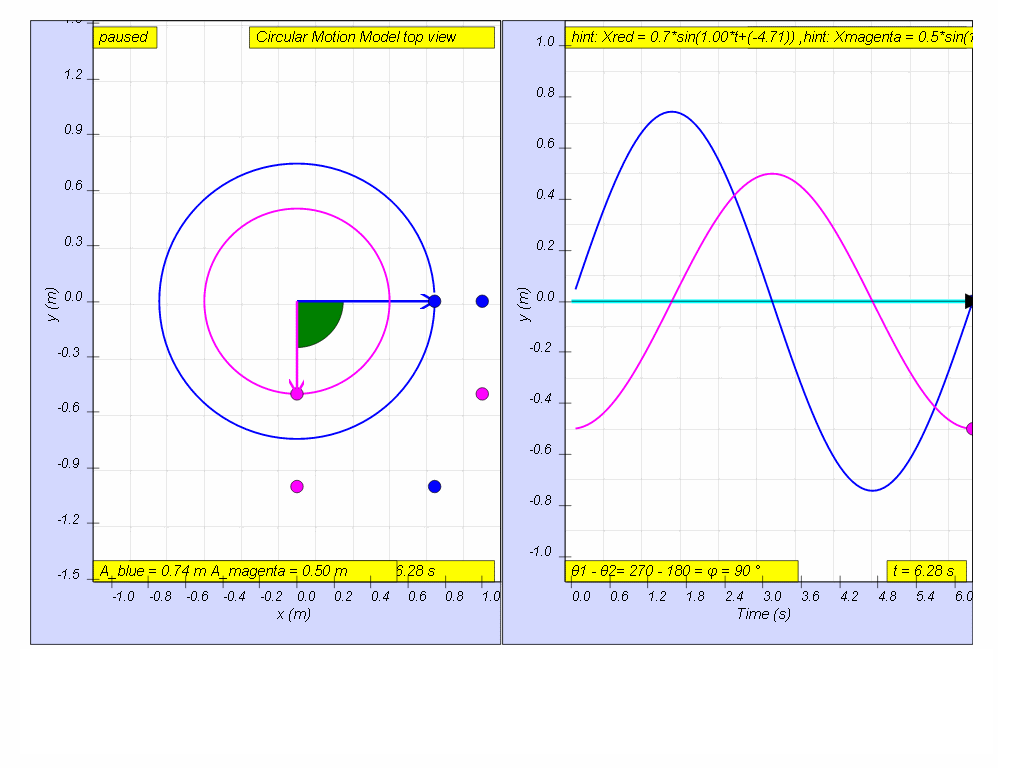
Q4: In, the diagram above, what is the phase difference between blue and magenta color y direction motion?

A4: the phase difference is 90 degrees, or more precisely blue lead red by 90 degrees angle.

1.1.3.2.3.1 YouTube:

http://youtu.be/0IaKcqRw_Ts This video shows how a pendulum's oscillations and the shadow of rotating object are related. This could be used to demonstrate that the projection of a circular motion is actually a simple harmonic motion.

1.1.3.2.3.2 Run Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/89

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.; Fu-Kwun Hwang

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM045/SHM045_Simulation.xhtml

Briefing Document: ⚛️Circular Motion and Simple Harmonic Motion Simulation

1. Overview

This document summarizes key concepts and information from a resource titled "10.1.3.2.3 Circular Motion Model and Relationship to Simple Harmonic Motion JavaScript HTML5 Applet Simulation Model" found on the Open Educational Resources / Open Source Physics @ Singapore website. The resource focuses on explaining the connection between uniform circular motion and simple harmonic motion, utilizing an interactive simulation built with Easy JavaScript Simulation (EJS).

2. Main Themes and Key Ideas

• Uniform Circular Motion and SHM: The core concept is that simple harmonic motion can be understood as the one-dimensional projection of uniform circular motion. This means that if an object moves in a circle at a constant speed, its shadow or projection along the x or y axis will exhibit simple harmonic motion.
• Mathematical Representation: The resource emphasizes the mathematical relationships. The position of an object in uniform circular motion can be represented by:
• x = A cos(ωt)
• y = A sin(ωt) Where:
• A is the radius of the circle (amplitude of the SHM).
• ω is the angular speed (angular frequency of the SHM).
• t is time.
• SHM Equations from Circular Motion: The document highlights that both the x and y components of the circular motion satisfy the defining relationship of SHM, expressed as second-order differential equations:
• d²x/dt² = -ω²x
• d²y/dt² = -ω²y These equations show that the acceleration of the projected motion is proportional to the displacement from the equilibrium point and in the opposite direction, which is the defining characteristic of SHM.
• Phase Difference: The resource points out that the x and y projections of the uniform circular motion have a phase difference of 90 degrees. Specifically, it mentions: "the phase difference is 90 degrees, or more precisely blue lead red by 90 degrees angle." This means that the x and y components reach their maximum and minimum displacements at different times.
• Interactive Simulation: The resource includes an embedded JavaScript HTML5 applet simulation model that visually demonstrates the concepts. The link to the simulation is included, allowing users to directly interact with the model. The user is encouraged to run the model to better understand the concepts.
• Educational Applications: The resource is intended for educational use, particularly at the junior college level, and is designed to be accessible on various platforms such as Windows, MacOSX, Linux, and Android/iOS devices.

3. Key Facts and Quotes

• Definition of SHM as projection of circular motion: "Simple harmonic motion can in some cases be considered to be the one-dimensional projection of uniform circular motion."
• Mathematical equations: "a circular motion can be described by x = A cos(ω t) and y A sin(ω t)"
• Differential equations for SHM: "both x = A cos(ω t) and y A sin(ω t) each follow the defining relationship for SHM as ordinary differential equations of d 2 x d t 2 = - ω 2 x and d 2 y d t 2 = - ω 2 y respectively."
• Phase difference: "the phase difference is 90 degrees, or more precisely blue lead red by 90 degrees angle."
• Video relation to pendulum: "This video shows how a pendulum's oscillations and the shadow of rotating object are related. This could be used to demonstrate that the projection of a circular motion is actually a simple harmonic motion."

4. Key Questions and Answers

The document includes questions and answers that guide the user to understand the concepts: * Q1: "given that, a circular motion can be described by x = A cos(ω t) and y A sin(ω t) what is the y-component model-equation that can describe the motion of a uniform circular motion?" * A1: "y = Asin (ωt)" * Q2: "When the x-component of the circular motion is modelled by x = A cos(ω t) and y A sin(ω t) suggest an model-equation for y." * A2: "y = Acos (ωt) for top position or y = - Acos (ωt) for bottom position" * Q3: "Explain why are the models for both x and y projection of a uniform circular motion, a simple harmonic motion?" * A3: "both x = A cos(ω t) and y A sin(ω t) each follow the defining relationship for SHM as ordinary differential equations of d 2 x d t 2 = - ω 2 x and d 2 y d t 2 = - ω 2 y respectively." * Q4: "In, the diagram above, what is the phase difference between blue and magenta color y direction motion?" * A4: "the phase difference is 90 degrees, or more precisely blue lead red by 90 degrees angle."

5. Resources

• Interactive Simulation Link: The document provides a link to run the simulation which is crucial for visual understanding. http://iwant2study.org/ospsg/index.php/89
• YouTube Video: A link to a YouTube video that connects pendulum oscillations with the projection of a rotating object, further explaining the relation between circular and simple harmonic motion. http://youtu.be/0IaKcqRw_Ts
• Additional Resources: This includes text and version information, as well as links to other related materials on the website.

6. Broader Context

The resource is part of a larger collection of Open Educational Resources at the website, which covers a broad range of physics topics, as evidenced by the extensive list of links on the page. This suggests a concerted effort to provide interactive, accessible learning materials. The presence of tags like "Junior College," "EasyJavaScriptSimulation," and various platform compatibility indicates the target audience and technological focus.

7. Conclusion

This resource effectively explains the relationship between uniform circular motion and simple harmonic motion using mathematical models, interactive simulations, and supporting videos. The interactive approach makes the abstract concepts more accessible and engaging for students. The resource's availability on multiple platforms enhances its usability in diverse learning environments.

Circular Motion and Simple Harmonic Motion Study Guide

Quiz

Instructions: Answer the following questions in 2-3 sentences each.

1. If the x-component of a circular motion is modeled by x = A cos(ωt), what does 'A' represent in this equation, and what does it physically correspond to?
2. Explain how the angular speed (ω) of an object in uniform circular motion relates to the frequency of its corresponding simple harmonic motion.
3. If an object's motion along the y-axis is modeled as y = A sin(ωt), how would the model equation change to represent the y-component of a circular motion starting at the bottom position?
4. Describe what is meant by "phase difference" in the context of simple harmonic motion, and provide an example using the provided source material.
5. The provided resource mentions that simple harmonic motion can be viewed as a "one-dimensional projection" of circular motion. Explain what this means.
6. What evidence in the source material suggests that the motion of a pendulum can be related to simple harmonic motion?
7. According to the source material, what mathematical property defines the relationship between the position of an object in SHM and its second derivative?
8. How does the JavaScript applet simulation model mentioned in the text aid in the understanding of the relationship between circular and simple harmonic motion?
9. Based on the source material, are the simulations only for desktop computers or are there other devices they can be used on?
10. Name at least one type of physics concept, beyond simple harmonic motion, that is mentioned in the listed resources that could be explored using these simulation models.

Quiz Answer Key

1. 'A' represents the amplitude of the circular motion, which is the radius of the circle. Physically, this corresponds to the maximum displacement of the object from the center of the circle or the equilibrium point in SHM.
2. The angular speed (ω) in uniform circular motion is equivalent to the angular frequency of the simple harmonic motion. It determines how quickly the object oscillates in SHM or the rate at which the object moves in the circular path.
3. To represent the y-component of a circular motion starting at the bottom position, the model equation would become y = -Acos(ωt). This change introduces a phase shift, reflecting the starting position of the oscillator.
4. Phase difference refers to the difference in angular position between two oscillating motions. In the provided material, the blue and magenta colored y-direction motions have a phase difference of 90 degrees, with the blue motion leading the red motion.
5. The "one-dimensional projection" means that the shadow or the component of a circular motion on a single axis (either x or y) executes simple harmonic motion, thus SHM is the behavior you see along a single dimension.
6. The YouTube video linked in the resource shows how the oscillations of a pendulum and the shadow of a rotating object are related, demonstrating that a pendulum’s motion can be considered a type of SHM.
7. The defining relationship is given by the differential equation d²x/dt² = -ω²x or d²y/dt² = -ω²y. This equation shows that the second derivative of the position is proportional to the negative of the position, with the constant of proportionality being ω².
8. The JavaScript applet simulation models provide a visual and interactive way to observe how the projection of a circular motion results in simple harmonic motion, helping to reinforce the conceptual link.
9. The simulations can be used on multiple devices including Android/iOS devices, handphones, tablets, iPads, Windows, MacOSX, Linux laptops, desktops, and Chromebook laptops as described under the model description.
10. Besides simple harmonic motion, the resource list includes resources that explore concepts such as projectile motion, wave superposition, electromagnetic induction, gravitational fields, and special relativity using simulation models.

Essay Questions

Instructions: Answer the following questions in essay format. Each essay should be multiple paragraphs in length, providing a detailed and comprehensive answer.

1. Explain how the uniform circular motion model provides a way to visualize and understand the relationships between key parameters of simple harmonic motion (SHM), such as amplitude, frequency, phase, and the relationship between position, velocity, and acceleration?
2. Analyze the educational value of using interactive simulations, such as the JavaScript applet model provided, in teaching the connection between circular motion and simple harmonic motion. How do these tools enhance student understanding compared to traditional methods?
3. Discuss how the concept of phase difference arises naturally from the circular motion model, and explain why understanding this concept is crucial to a complete understanding of simple harmonic motion.
4. The text provides a variety of simulation tools for physics concepts. Compare and contrast how the circular motion and SHM simulations might be used to teach a concept, and suggest ways these interactive models can encourage students to explore deeper physical principles.
5. The source text lists a multitude of models for different physics and math concepts. How can these simulations, especially in the context of open educational resources, potentially revolutionize physics and mathematics education?

Glossary

• Simple Harmonic Motion (SHM): A type of periodic motion where the restoring force is directly proportional to the displacement and acts in the opposite direction. The result is a repetitive oscillation around an equilibrium position.
• Uniform Circular Motion: Motion of an object along a circular path at a constant speed.
• Angular Speed (ω): The rate at which an object rotates or revolves, measured in radians per second.
• Amplitude (A): The maximum displacement of an object from its equilibrium position during oscillation or the radius of the circular path for uniform circular motion.
• Phase Difference: The difference in angular position between two oscillating motions, measured in degrees or radians.
• One-Dimensional Projection: The shadow or component of a two-dimensional motion (like circular motion) onto a single axis (x or y), resulting in a one-dimensional motion.
• JavaScript Applet: A small application written in JavaScript that can be embedded in a webpage to create interactive simulations or content.
• Open Educational Resources (OER): Freely available teaching, learning, and research materials that reside in the public domain or have been released under an open license.
• Differential Equation: A mathematical equation that relates a function to its derivatives. It is used here to define SHM.
• Equilibrium Position: The stable position for an object where there is no net force acting on it. In SHM it's the center point around which oscillations happen.

 What is in Phase?

 

Video

 Version:

1. http://weelookang.blogspot.sg/2016/07/why-is-in-phase.html
   

Other Resources

[text]

FAQ

• Q1: How can uniform circular motion be related to simple harmonic motion (SHM)?
• A1: Simple harmonic motion can be understood as the one-dimensional projection of uniform circular motion. Imagine an object moving in a circle at a constant speed. If you look at the object's position only along one axis (either the x-axis or y-axis), that movement will follow the pattern of SHM.
• Q2: If the x-component of a uniform circular motion is described by x = Acos(ωt), what are possible model-equations for the y-component?
• A2: The y-component can be modeled as y = Asin(ωt). Alternatively, if starting at the top or bottom of the circle, the y component could be modeled as y = Acos(ωt) or y = -Acos(ωt), respectively. The key difference between the x and y components in the context of circular motion are the sine and cosine functions, which are out of phase with each other by 90 degrees.
• Q3: Why are both the x and y projections of uniform circular motion considered examples of simple harmonic motion?
• A3: The mathematical relationships for both x and y projections align with the defining characteristic of SHM. Specifically, their motion can be described by second-order ordinary differential equations: d²x/dt² = -ω²x and d²y/dt² = -ω²y. These equations show that the acceleration is proportional to and in the opposite direction of the displacement, which is the hallmark of SHM.
• Q4: What is the phase difference between the y-direction motion modeled by y = Asin(ωt) and y = Acos(ωt)?
• A4: The phase difference is 90 degrees. Specifically, y = Asin(ωt) leads y = Acos(ωt) by a 90-degree angle. In practical terms, it can be thought of as one oscillation starting a quarter-cycle later than the other.
• Q5: What type of resources are available on this site besides the simulation of the circular motion model?
• A5: This site offers a variety of interactive simulations and learning tools, including simulations related to:
• Simple harmonic motion (spring-mass systems, pendulums)
• Gravitational fields and potential
• Electromagnetism
• Kinematics
• Wave phenomena
• Vector addition
• Various math based games and tools. These simulations cover a wide range of topics, suitable for different educational levels, ranging from primary school to junior college level.
• Q6: What platforms are compatible with these simulations and interactive tools?
• A6: The simulations, built using Easy JavaScript Simulation (EJS), are designed to be compatible with various platforms, including:
• Android/iOS devices (including phones, tablets, and iPads)
• Windows/MacOSX/Linux systems (including laptops and desktops)
• ChromeBook laptops. This ensures broad accessibility of these educational resources on different devices and operating systems.
• Q7: What is the primary programming language behind these interactive simulations?
• A7: The simulations are built using Easy JavaScript Simulation (EJS), which is a framework that employs JavaScript and HTML5 for creating interactive, web-based simulations. This combination makes the resources easily deployable within a web browser without requiring additional plugins, enabling smooth cross-platform usage.
• Q8: Are these resources freely available for educational use?
• A8: Yes, the resources are available under a Creative Commons Attribution-Share Alike 4.0 Singapore License, making them free to use, share, and adapt for non-commercial educational purposes. For commercial use of the EasyJavaScriptSimulations Library, you must contact them directly.