About

1.6.4 Applications of Critical Damping

Factors that affects the damping coefficient b includes the drag in the oscillating spring-mass system that takes energy out of the system as heat loss etc.

therefore, the higher the viscosity of the medium the system is in, the greater the drag coefficient b.

1.6.4.1    Car suspension

    The spring of a car’s suspension is critically damped so that when a     car goes over a bump, the passenger in the car quickly and smoothly     regains equilibrium.

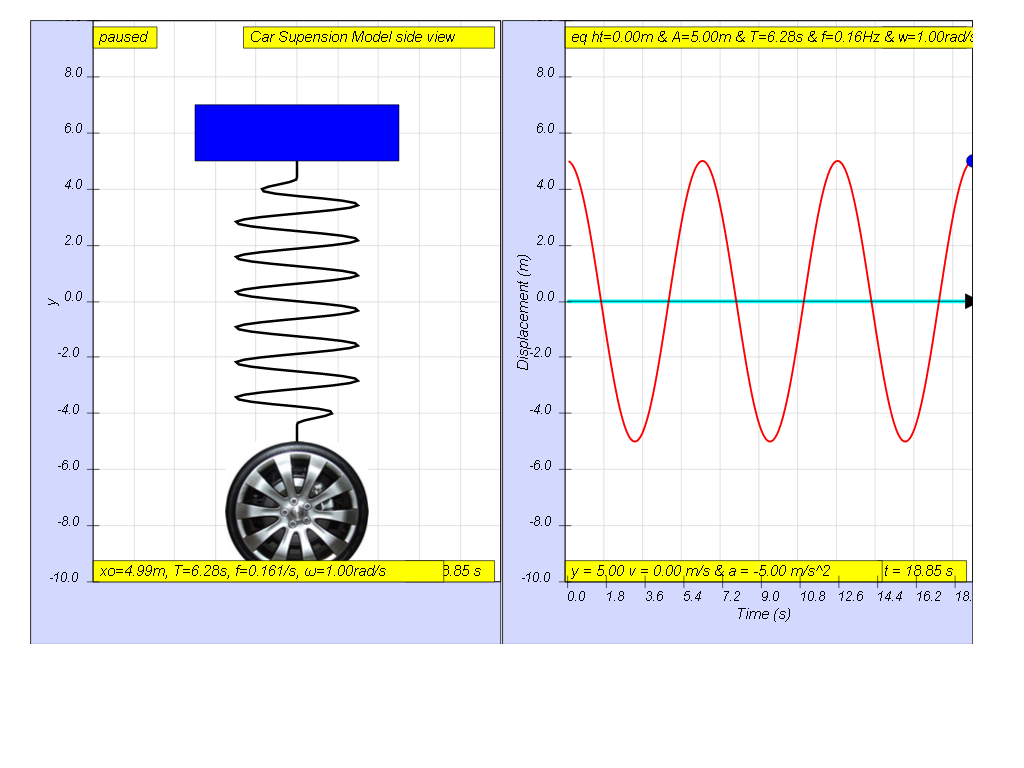
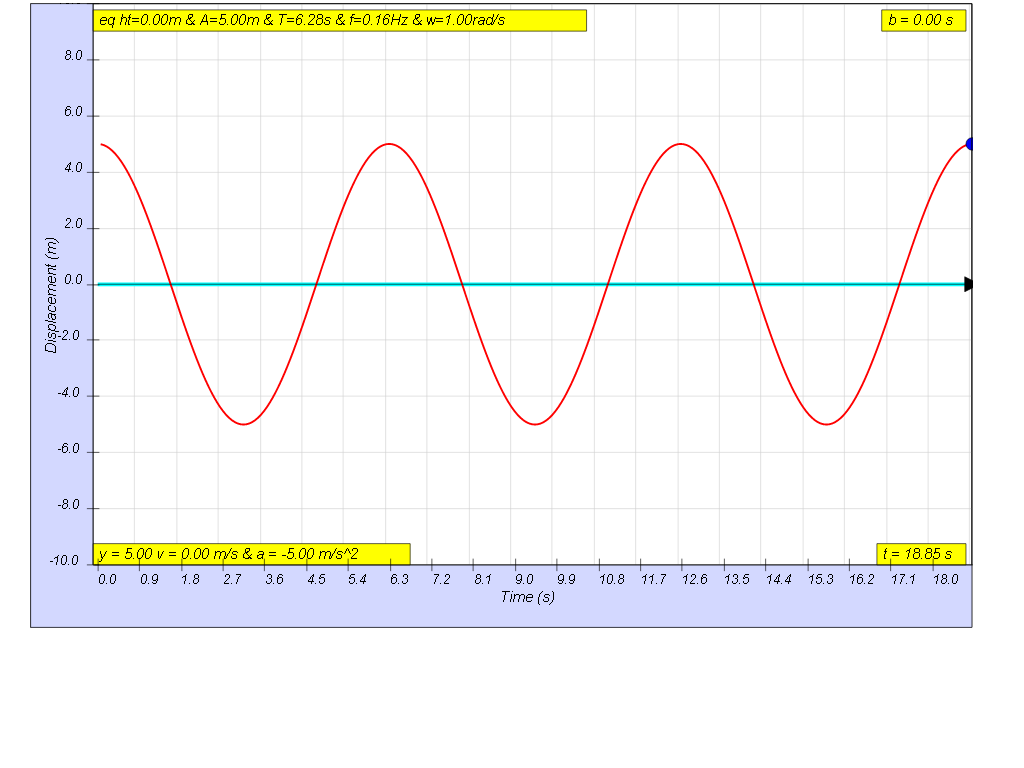
1.6.4.1.1 No Damping

the picture shows no damping case b = 0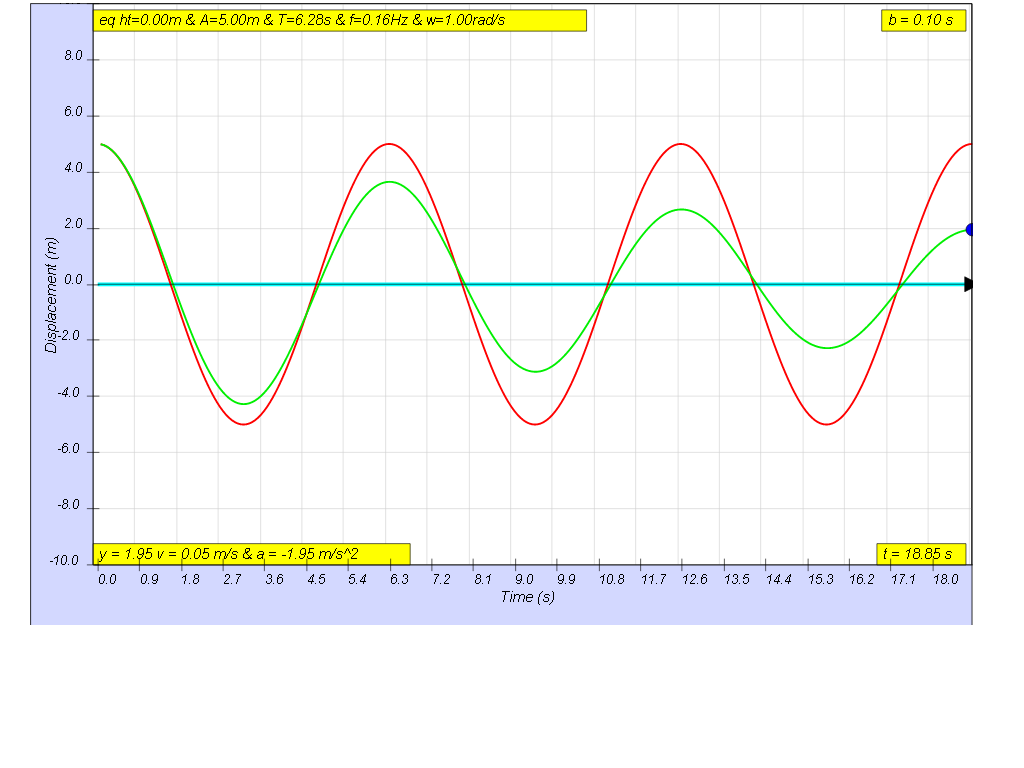

1.6.4.1.2 Light Damping 

the picture shows light damping case b = 0.1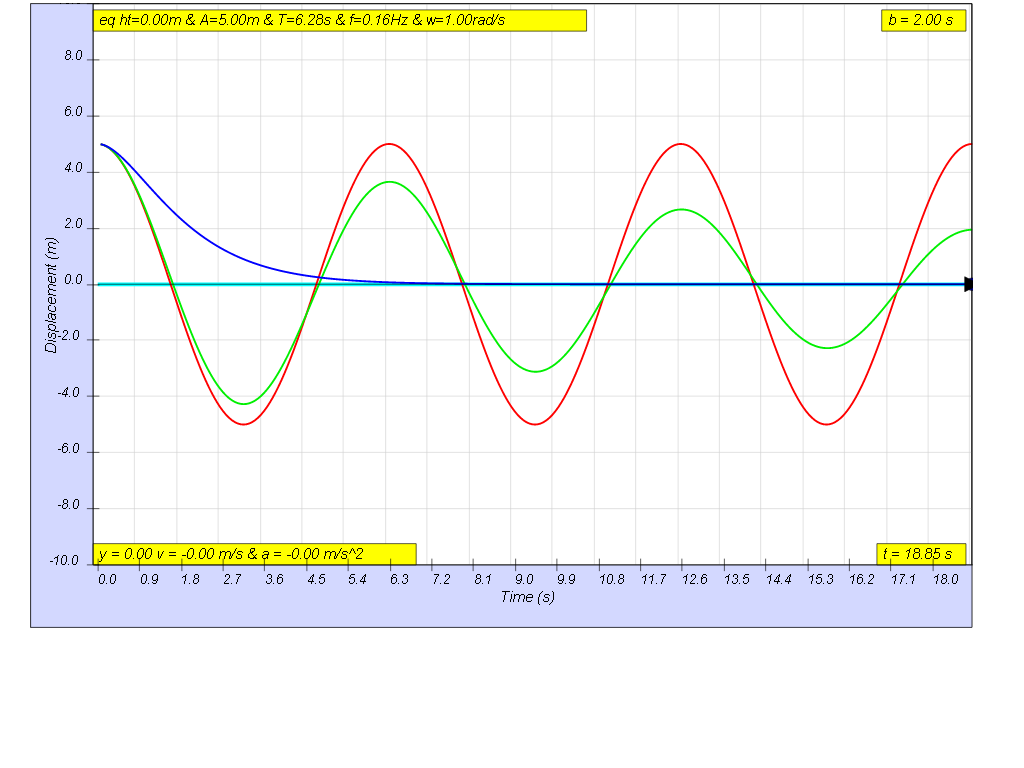

1.6.4.1.3 Critical Damping 

the picture shows critically damping case b = 2.0
However, car suspensions are often adjusted to slightly under critical damped condition to give a more comfortable ride. Critical damping also leaves the car ready to respond to further bumps in the road quickly.

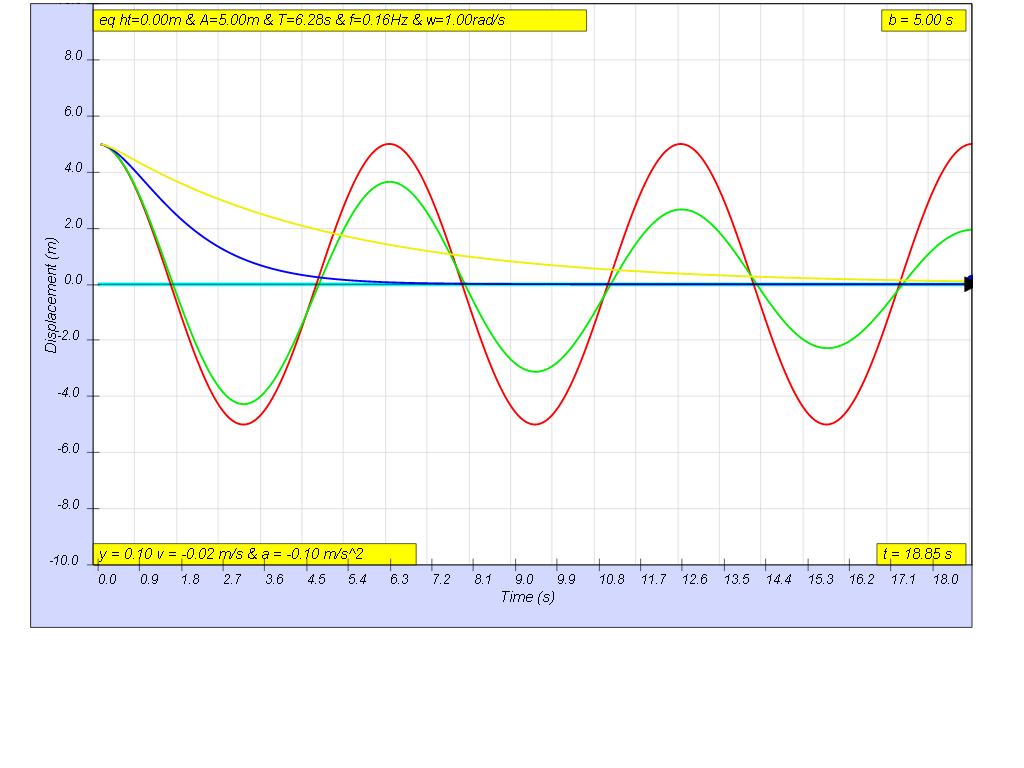
1.6.4.1.4 Heavy Damping 

the picture shows heavy damping case b = 5.0

1.6.4.1.5 Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/85

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM21/SHM21_Simulation.xhtml

Briefing Document: 🚗Car Suspension HTML5 Applet Simulation Model

1. Overview:

This document reviews an online interactive simulation model of car suspension, specifically focusing on the concept of damping and its effects on vehicle ride quality. The model, built using Easy JavaScript Simulation (EJS), is hosted on the Open Educational Resources / Open Source Physics @ Singapore platform. The resource is designed to be accessible on various devices (desktops, laptops, tablets, smartphones).

2. Main Themes:

• Damping in Oscillatory Systems: The core concept explored is the effect of damping on an oscillating spring-mass system, which is analogous to a car's suspension system. The document emphasizes that the damping coefficient (represented by 'b') controls how quickly the system returns to equilibrium after being disturbed (like going over a bump).
• Critical Damping and its Applications: A key focus is on critical damping, defined as the point where the system returns to equilibrium in the fastest possible time without oscillation. This is ideal for car suspensions to provide a comfortable and controlled ride. The resource states: "The spring of a car’s suspension is critically damped so that when a car goes over a bump, the passenger in the car quickly and smoothly regains equilibrium."
• Types of Damping: The resource examines different types of damping:
• No Damping (b=0): The system oscillates indefinitely with constant amplitude.
• Light Damping (b=0.1): The system oscillates with decreasing amplitude until it comes to rest.
• Critical Damping (b=2.0): The system returns to equilibrium quickly without oscillation.
• Heavy Damping (b=5.0): The system returns to equilibrium slowly without oscillation.
• Practical Adjustment: Slight Under-Damping: The document indicates that car suspensions are often "adjusted to slightly under critical damped condition to give a more comfortable ride." This implies a design compromise between rapid return to equilibrium and a smoother feel.
• Interactive Learning with Simulation: The use of an HTML5 applet enables interactive, hands-on learning. Students can directly observe the effect of different damping coefficients in a simulation.

3. Key Ideas and Facts:

• Damping Coefficient 'b': The value of 'b' is crucial in determining the behavior of the system. A higher 'b' value results in greater damping. "Factors that affects the damping coefficient b includes the drag in the oscillating spring-mass system that takes energy out of the system as heat loss etc."
• Viscosity and Drag: The document explains how the viscosity of the medium influences the damping coefficient: "therefore, the higher the viscosity of the medium the system is in, the greater the drag coefficient b."
• Purpose of Critical Damping: "Critical damping also leaves the car ready to respond to further bumps in the road quickly." This highlights the importance of rapid stabilization in a dynamic environment.
• Tradeoff between Comfort and Response: Adjusting the damping to be slightly under critical creates a more comfortable ride, but this comes at the cost of less rapid return to equilibrium than what is technically possible.

4. Supporting Quotes:

• "The spring of a car’s suspension is critically damped so that when a car goes over a bump, the passenger in the car quickly and smoothly regains equilibrium."
• "However, car suspensions are often adjusted to slightly under critical damped condition to give a more comfortable ride."
• "Critical damping also leaves the car ready to respond to further bumps in the road quickly."
• "Factors that affects the damping coefficient b includes the drag in the oscillating spring-mass system that takes energy out of the system as heat loss etc. therefore, the higher the viscosity of the medium the system is in, the greater the drag coefficient b."

5. Simulation Model Links:

• Embedded Model: The resource provides an embedded iframe code for integrating the simulation into a webpage:
• <iframe width="100%" height="100%" src="https://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM21/SHM21_Simulation.xhtml " frameborder="0"></iframe>
• Run Sim link: http://iwant2study.org/ospsg/index.php/85
• Apps: https://play.google.com/store/apps/details?id=com.ionicframework.shm21app525671&hl=en

6. Other Relevant Resources:

• The document lists numerous other simulations and learning resources, most notably related to spring mass models and harmonic motion.

7. Target Audience and Educational Value:

• The resource is targeted at Junior College (high school) students, and it covers a topic typically taught in introductory physics courses.
• It uses interactive simulation to create better comprehension of abstract concepts like damping, and real-world applications.
• The platform includes a huge range of interactive resources that span multiple disciplines.

8. Conclusion:

The "Car suspension HTML5 Applet Simulation Model" is a valuable educational resource that provides a practical and interactive way to understand the concept of damping and its application in car suspension systems. The different levels of damping (no, light, critical and heavy) are all explained, and the applet is interactive and easy to use. The site it is hosted on has many other simulations for a variety of subjects. The explanation of critical damping, and the practical consideration of slight under-damping for a more comfortable ride, are key learning points.

Car Suspension & Damping Study Guide

Quiz

1. What is the primary purpose of a car's suspension system?
2. Explain what is meant by "damping" in the context of a spring-mass system.
3. How does the viscosity of the medium affect the damping coefficient?
4. What is critical damping, and why is it important in car suspension?
5. Describe the behavior of a car suspension with no damping (b=0).
6. How does light damping affect the car's suspension response?
7. What is the consequence of heavy damping on a car's suspension?
8. Why are car suspensions often adjusted to be slightly under-critically damped?
9. According to the provided material, what is one of the main factors that affects the damping coefficient b?
10. Briefly describe the simulation model presented by the provided resource.

Quiz Answer Key

1. The primary purpose of a car's suspension system is to allow the passenger in the car to quickly and smoothly regain equilibrium when the car goes over a bump. This contributes to a more comfortable ride.
2. Damping is a process where energy is removed from an oscillating spring-mass system. This often occurs through heat loss and other forms of friction, eventually bringing the system to a state of equilibrium.
3. The higher the viscosity of the medium the system is in, the greater the drag coefficient b, meaning there is more resistance to movement which will result in more damping.
4. Critical damping is the ideal level of damping where a system returns to equilibrium as quickly as possible without oscillating. In car suspension, it ensures a smooth ride and responsiveness to further road bumps.
5. With no damping (b=0), the car's suspension would oscillate indefinitely after encountering a bump. There would be no way to restore equilibrium, resulting in a very bouncy ride.
6. Light damping leads to the car's suspension oscillating a few times before settling back to its equilibrium position. The oscillations decay, but are still present.
7. Heavy damping causes the car's suspension to return to equilibrium slowly, but without oscillation. The car would not respond quickly to bumps.
8. Car suspensions are often adjusted to be slightly under-critically damped to provide a more comfortable ride. The small amount of oscillation feels more natural and less jarring to the car's occupants than a critical damped response.
9. According to the text, one main factor that affects the damping coefficient b is the drag in the oscillating spring-mass system that removes energy as heat loss.
10. The simulation model presented is a HTML5 applet that demonstrates the effects of varying degrees of damping (no, light, critical, and heavy) on a car's suspension using a spring-mass model, illustrating how the car returns to equilibrium after encountering a bump.

Essay Questions

1. Analyze the impact of different damping coefficients on the comfort and performance of a car's suspension system. Include a discussion on how the ideal level of damping might vary based on different driving conditions.
2. Compare and contrast the behaviors of under-damped, critically damped, and over-damped systems in the context of mechanical oscillations. Use real-world examples beyond car suspensions to support your explanation.
3. Discuss the role of damping in energy dissipation and its implications for engineering applications. Explore how engineers strategically design damping systems to meet different requirements.
4. Using the car suspension model as a starting point, explore the broader principles of damped harmonic motion. How is the concept of damping applied in various fields (e.g., architecture, electronics, and biology)?
5. Considering the simulations and principles discussed, propose a novel damping system or mechanism, detailing the key factors and potential benefits of the proposal.

Glossary

Damping: The process by which energy is dissipated from an oscillating system, reducing the amplitude of its oscillations over time and eventually leading to equilibrium.

Damping Coefficient (b): A numerical value that quantifies the degree of damping in a system; a higher coefficient indicates greater damping. It is a measure of the drag in the system.

Critical Damping: The optimal level of damping where a system returns to equilibrium as quickly as possible without oscillating; also provides the fastest return to equilibrium for the system.

Equilibrium: A state of balance or rest, where a system is not undergoing any net change in its position or motion.

Oscillation: The repetitive variation, typically in time, of some measure about a central value or between two or more different states; a back and forth motion.

Viscosity: A measure of a fluid's resistance to flow; in the context of damping, higher viscosity implies a greater drag force and greater damping.

Spring-Mass System: A simplified model of an oscillating system, consisting of a mass attached to a spring, often used to study concepts like oscillation, damping, and simple harmonic motion.

Under-Damped: A condition where an oscillating system will swing back and forth past equilibrium multiple times before settling back into its equilibrium position.

Over-Damped: A condition in an oscillating system where the system will slowly move back to equilibrium without oscillating.

Drag Coefficient: In the context of damping, the drag coefficient is the numerical representation of the force of resistance encountered by a system as it moves within a viscous medium. A higher coefficient indicates a larger opposing force.

Apps

https://play.google.com/store/apps/details?id=com.ionicframework.shm21app525671&hl=en

 Other resources

https://www.geogebra.org/m/ev62ku7w by tan Seng kwang

Frequently Asked Questions about Car Suspension and Damping

1. What is the purpose of a car's suspension system? A car's suspension system is designed to isolate the car's body from the bumps and irregularities of the road surface. This ensures a smoother, more comfortable ride for the passengers. It uses a combination of springs and dampers (often called shock absorbers) to achieve this. When the car hits a bump, the spring compresses and the damper dissipates the energy to prevent excessive bouncing.
2. What is meant by damping in the context of car suspension? Damping refers to the mechanism that dissipates energy from the suspension system's oscillations, preventing it from bouncing up and down uncontrollably. This is usually achieved through the use of a damper (shock absorber), which introduces a force that opposes the motion of the spring. The level of damping is crucial for the car’s handling and passenger comfort.
3. What are the different types of damping and how do they affect a car's ride? There are several types of damping, including:

• No Damping: The suspension system would oscillate indefinitely after encountering a bump. This results in a very bouncy ride and is impractical.
• Light Damping: The oscillations will die down eventually, but it takes a long time, resulting in a bouncy and potentially uncomfortable ride.
• Critical Damping: The suspension returns to its equilibrium position as quickly as possible without overshooting or oscillating. This provides a smooth and efficient response to disturbances.
• Heavy Damping: The suspension returns to equilibrium slowly, resulting in a sluggish response that can also be uncomfortable.

1. What is critical damping, and why is it important in car suspension? Critical damping is the ideal level of damping where the suspension returns to its equilibrium position in the shortest time possible without any oscillations or bouncing. It prevents the car from continuing to bounce after hitting a bump, providing a stable, comfortable, and responsive driving experience. In practical terms it provides a good compromise between comfort and response.
2. Why are car suspensions often designed to be slightly under-critically damped? While critical damping would be ideal in theory, car suspensions are often adjusted to be slightly under-damped for a more comfortable feel. This allows for a small amount of oscillation which some perceive as more comfortable. A slightly under-damped system is also more quickly ready to react to subsequent bumps compared to a critically damped system that has just returned to equilibrium.
3. What factors influence the damping coefficient? The damping coefficient (often represented by 'b' in physics equations) is influenced by the amount of resistance experienced by the oscillating spring-mass system. One of the major factors is the viscosity of the medium in which the system is operating. For car suspensions, this usually refers to the oil within the shock absorbers or the air resistance within the system. The higher the viscosity or resistance, the greater the damping coefficient. This means more energy is dissipated as heat rather than causing further oscillation.
4. How can the principles of damping and oscillations be visualized or explored using simulations? Simulations using tools like Easy JavaScript Simulation (EJS) and GeoGebra are useful to visualize and explore the concepts of damping and oscillations. These tools enable users to manipulate parameters like the damping coefficient and observe the resulting motion, helping them understand the concepts more intuitively. They allow observation of the effects of under damping, critical damping, and over damping in a dynamic way.
5. Beyond car suspensions, where else are damping principles applied? The concept of damping is widely used in various fields, including:

• Mechanical Engineering: Dampers are essential in structures and machines to reduce unwanted vibrations and noise.
• Electronics: Damping circuits are used to control the flow of energy and prevent instability.
• Civil Engineering: Dampers are used to protect buildings and bridges from earthquakes and strong winds.
• Musical Instruments: Damping is essential in instruments to control the decay of sound. The fundamental principles explored in a car suspension apply to many different types of oscillatory systems where a specific response is desired.