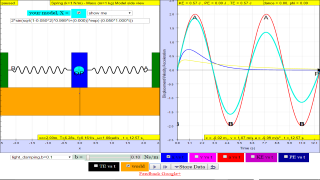
About

1.6 Degrees of damping                    LO (i)

If no frictional forces act on an oscillator (e.g.  mass-spring system, simple pendulum system,  etc.), then it will oscillate indefinitely.

In practice, the amplitude of the oscillations decreases to zero as a result of friction. This type of motion is called damped harmonic motion. Often the friction arises from air resistance (external damping) or internal forces (internal damping).

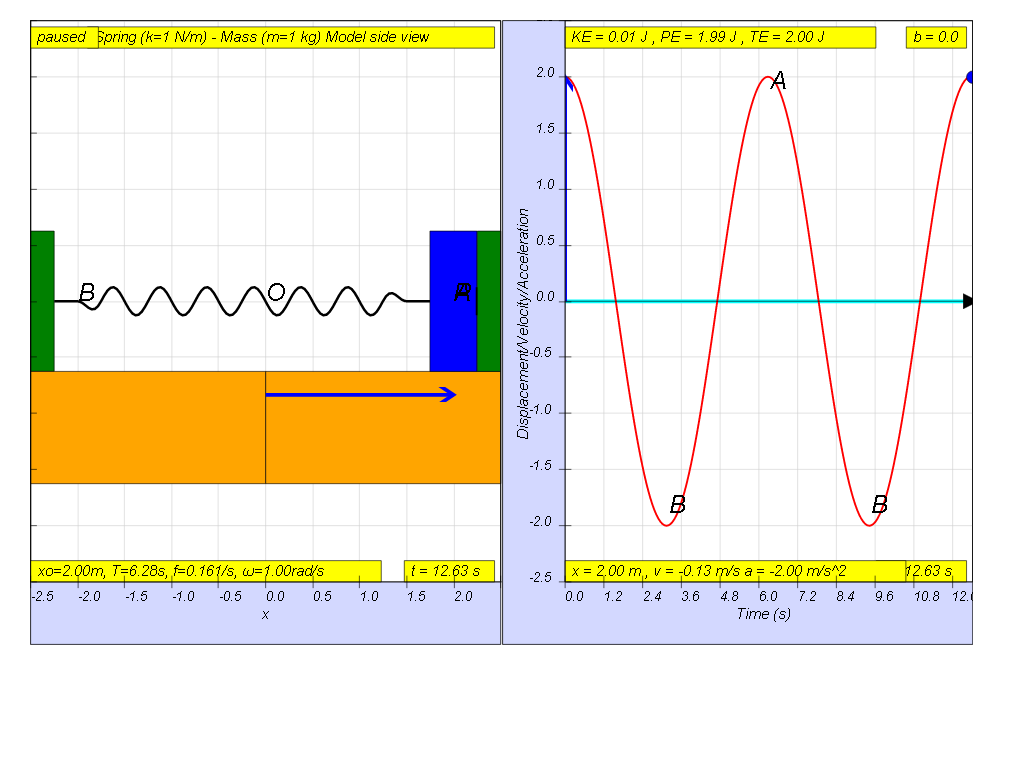
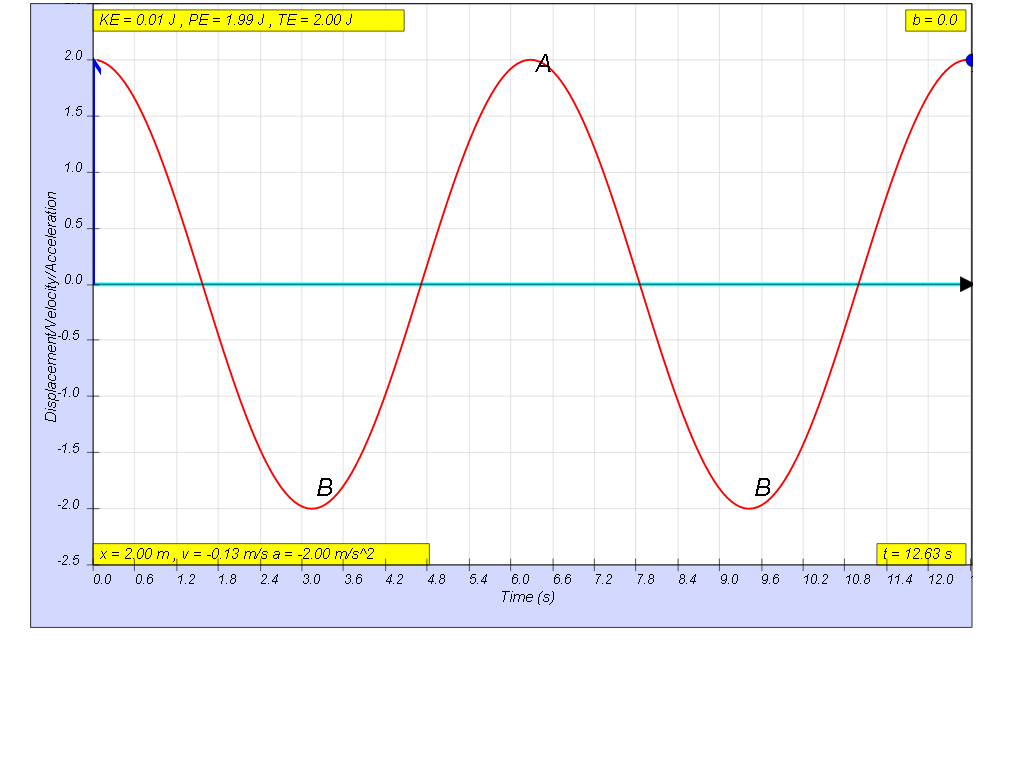
1.6.1 if the motion is x= x₀ sin(ωt), the following are the x vs t graphs for 2 periods, as an illustration of the damping.

1.6.1.1 No damping

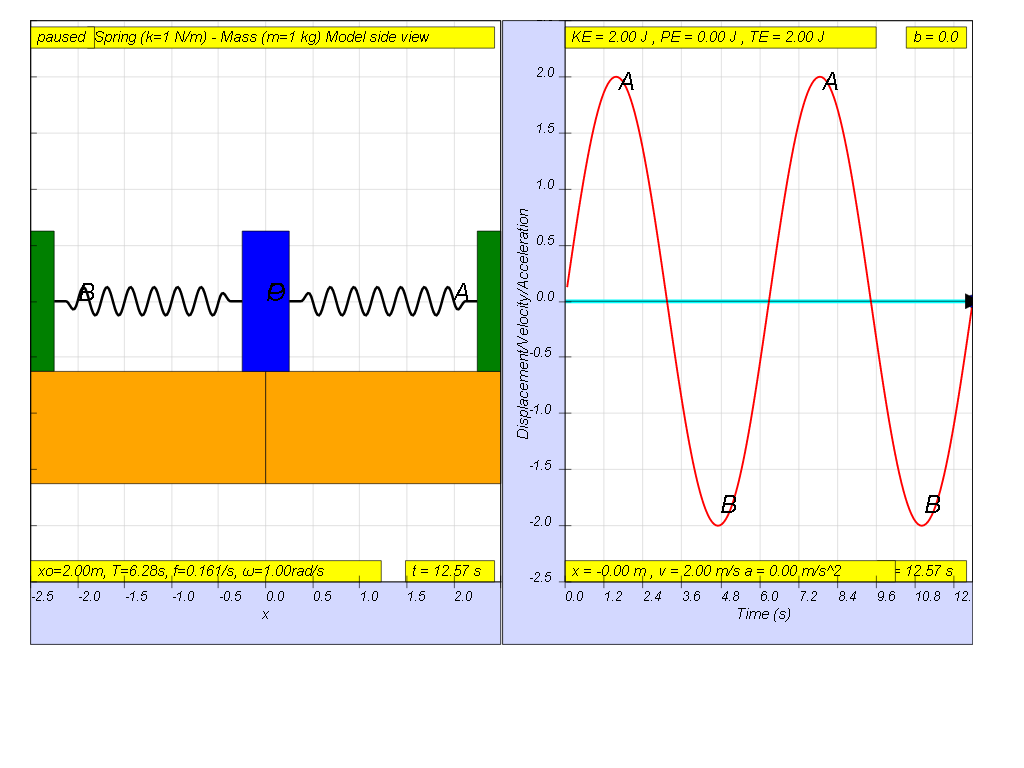
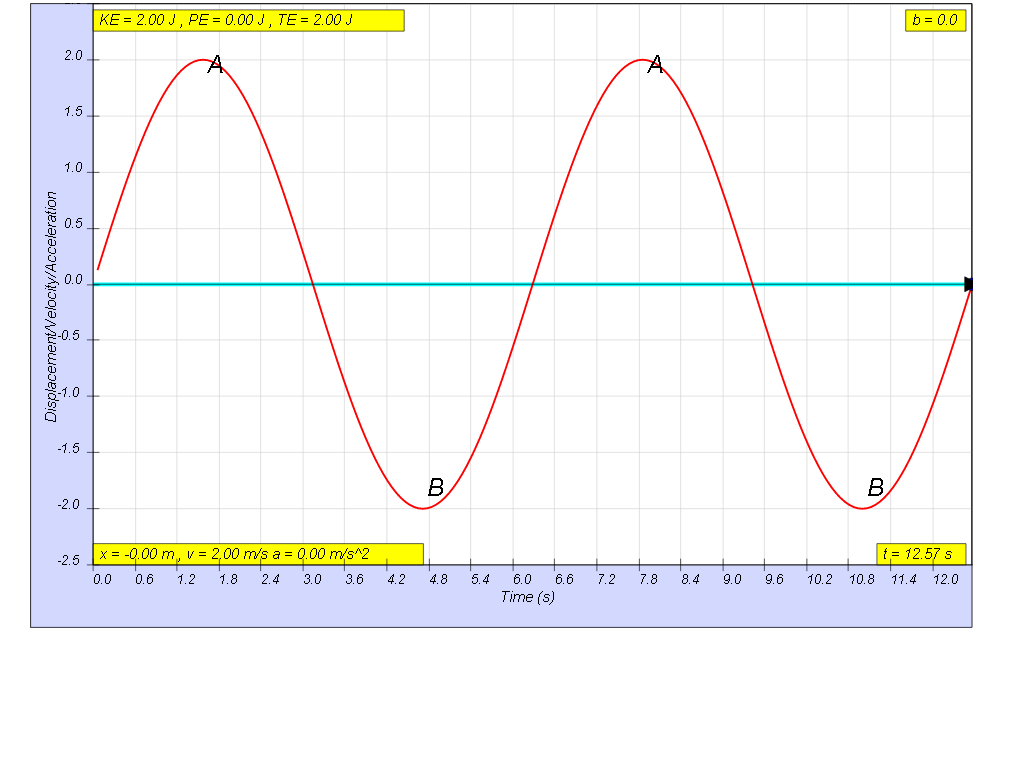
when b=0.0 no damping, system oscillates forever without coming to rest. Amplitude and thus total energy is constant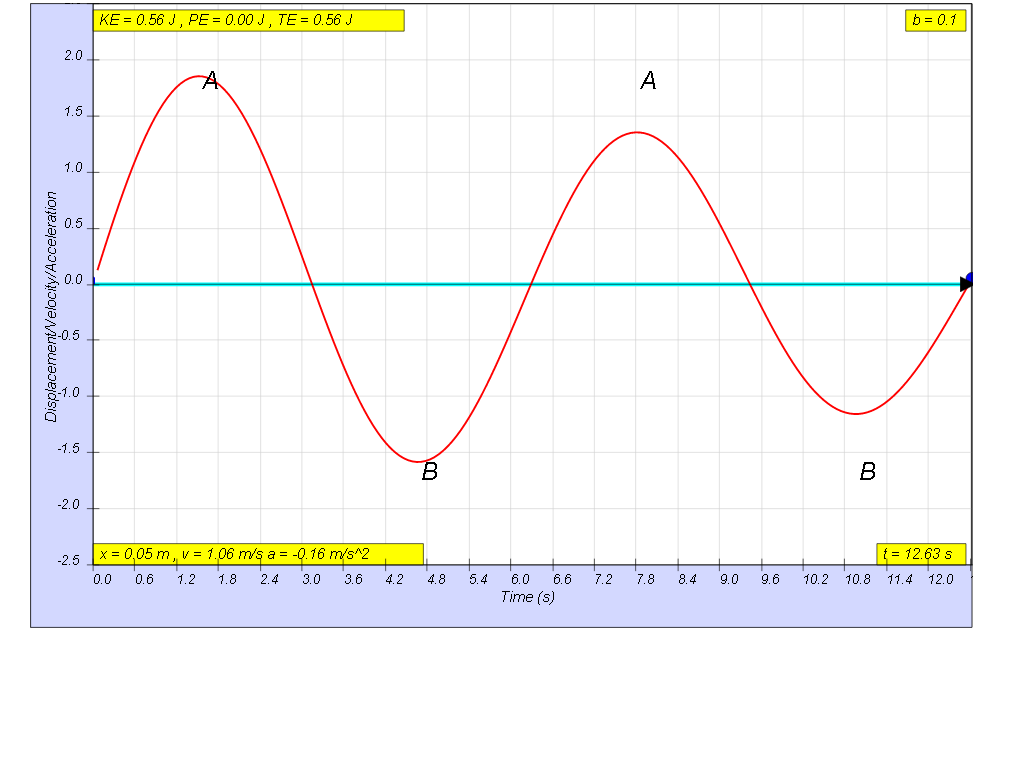

1.6.1.2 Light damping

when b=0.1 very lightly damp, system undergoes several oscillations of decreasing amplitude before coming to rest. Amplitude of oscillation decays exponentially with time.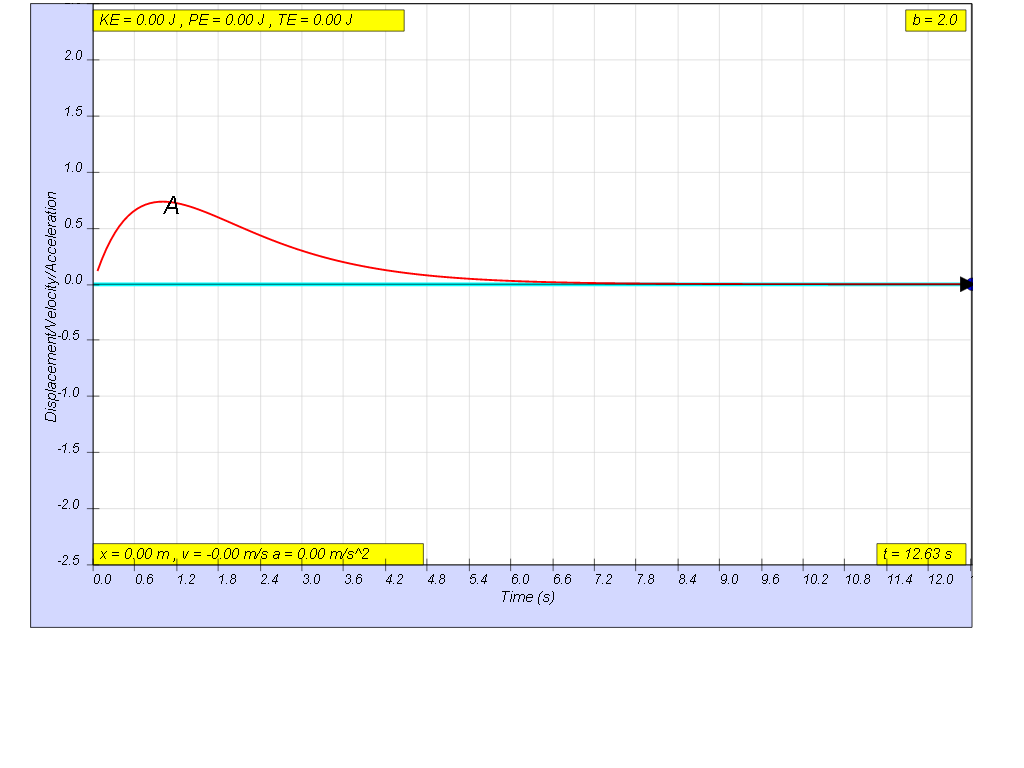

1.6.1.3 Critical damping

when b=2.0, critically damp system returns to equilibrium in the minimum time, without overshooting or oscillating about the equilibrium position amplitude.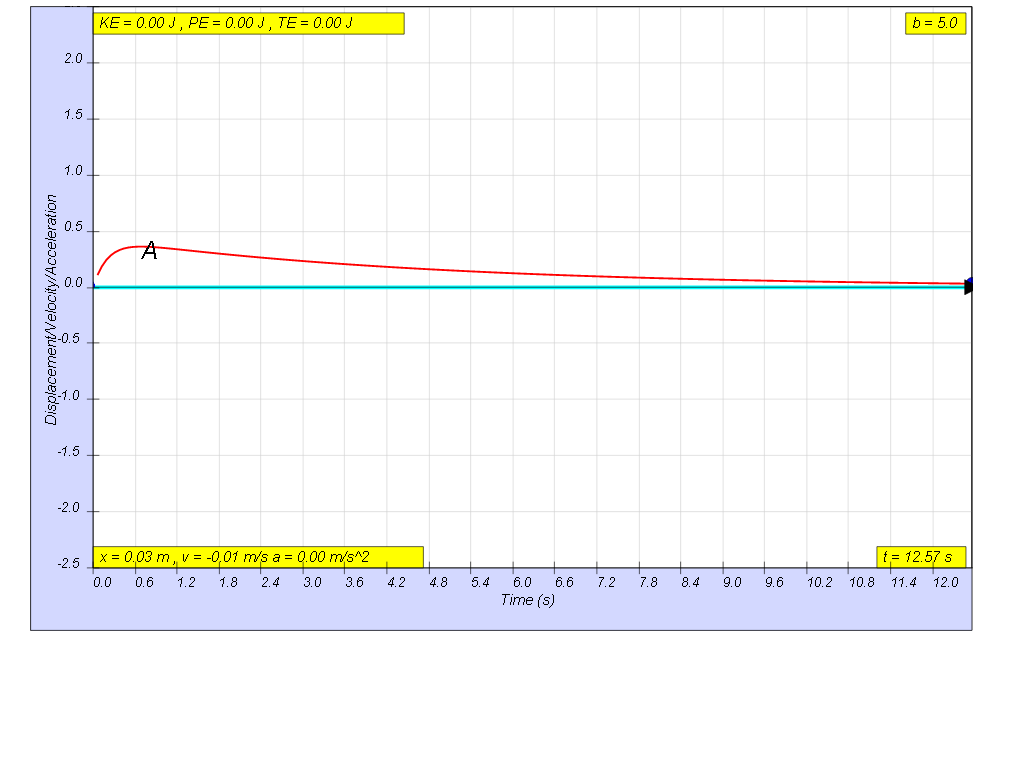

1.6.1.4 Heavy damping

when b=5.0, very heavy damp, system returns to equilibrium very slowly without any oscillation

1.6.2 a more typical starting position, is  x= x₀ cos(ωt), the following are the x vs t graphs for 2 periods, as an illustration of the damping.

1.6.2.1 No damping

when b=0.0 no damping, system oscillates forever without coming to rest. Amplitude and thus total energy is constant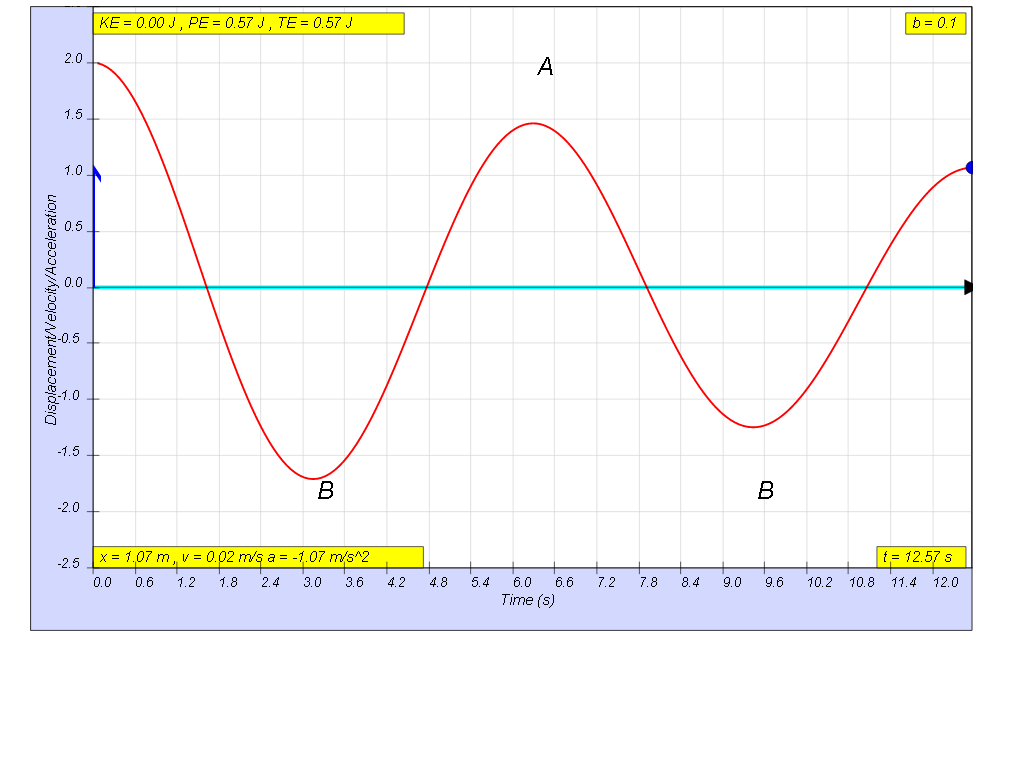

1.6.2.2 Light damping

when b=0.1 very light damping, system undergoes several oscillations of decreasing amplitude before coming to rest. Amplitude of oscillation decays exponentially with time.

1.6.2.3 Critical damping

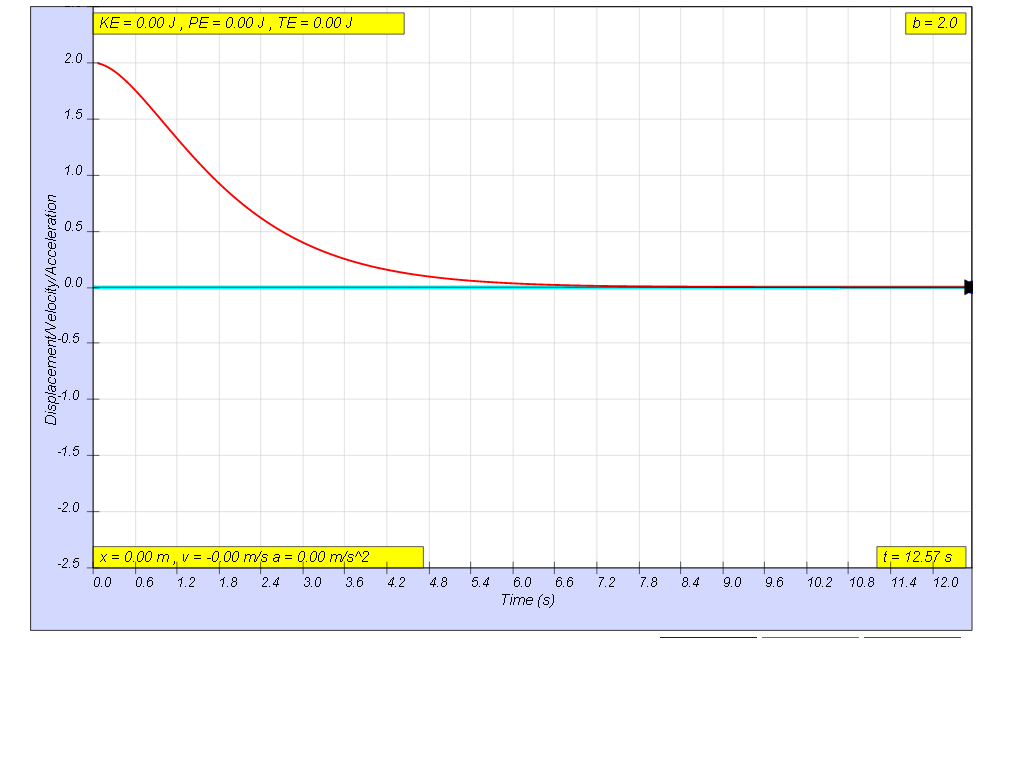
when b=2.0 critically damp, system returns to equilibrium in the minimum time, without overshooting or oscillating about the equilibrium position amplitude.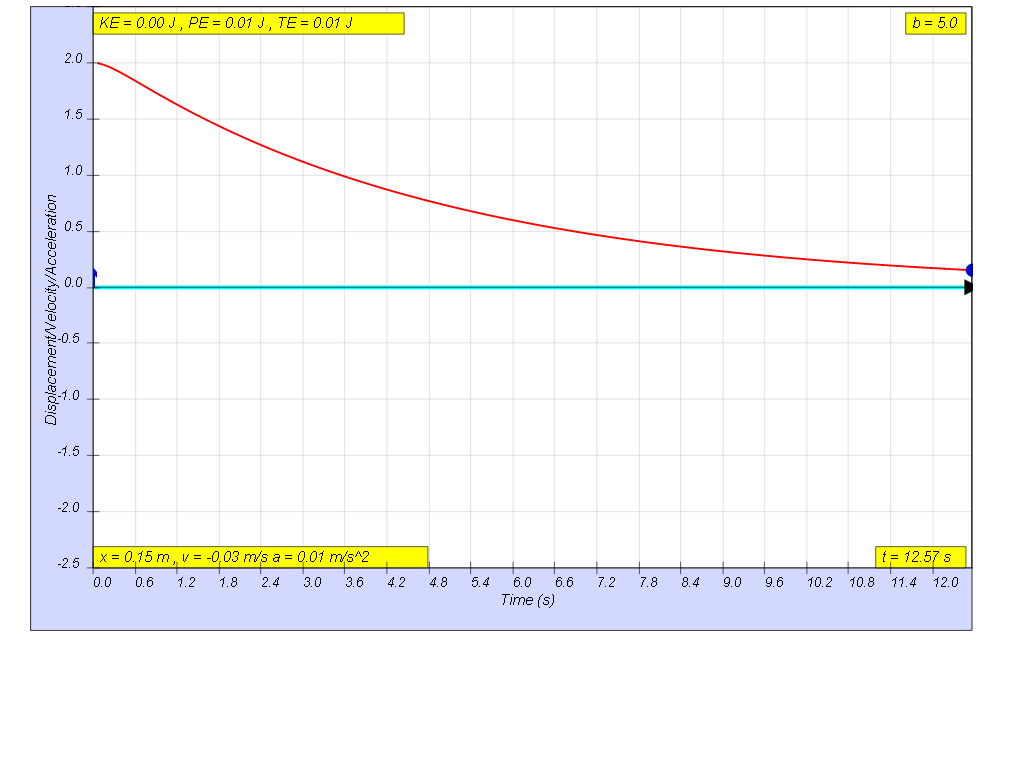

1.6.2.4 Heavy damping

when b=5.0 very heavy damp,  system returns to equilibrium very slowly without any oscillation.

1.6.3 Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/84

 

Translations

Code	Language		Translator	Run

Credits

lookang

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM20/SHM20_Simulation.xhtml

Briefing Document: 📈10.6 Degrees of Damping HTML5 Applet Simulation Model

1. Overview:

This document analyzes an online resource from "Open Educational Resources / Open Source Physics @ Singapore" which features an interactive simulation titled "10.6 Degrees of Damping HTML5 Applet Simulation Model." The resource focuses on illustrating the concept of damped harmonic motion, a crucial topic in physics, particularly for junior college students. The simulation is built using EasyJavaScriptSimulation (EJS) and is accessible on various platforms including web browsers, Android/iOS devices, and desktop operating systems.

2. Main Themes and Concepts:

• Damped Harmonic Motion: The core concept explored is damped harmonic motion. This is the oscillation of a system where the amplitude decreases over time due to frictional forces. The document explains: "If no frictional forces act on an oscillator... then it will oscillate indefinitely. In practice, the amplitude of the oscillations decreases to zero as a result of friction. This type of motion is called damped harmonic motion."
• Frictional Forces and Damping: The document identifies two primary sources of friction leading to damping: air resistance (external damping) and internal forces (internal damping).
• Simulation Parameters & Damping Levels: The simulation allows users to observe the effects of varying levels of damping on the oscillatory motion. It uses a parameter 'b' to control the damping coefficient. Four key damping scenarios are presented:
• No Damping (b=0.0): "system oscillates forever without coming to rest. Amplitude and thus total energy is constant."
• Light Damping (b=0.1): "system undergoes several oscillations of decreasing amplitude before coming to rest. Amplitude of oscillation decays exponentially with time."
• Critical Damping (b=2.0): "system returns to equilibrium in the minimum time, without overshooting or oscillating about the equilibrium position amplitude."
• Heavy Damping (b=5.0): "system returns to equilibrium very slowly without any oscillation."
• Initial Conditions and Graph Representation: The document emphasizes how the initial condition (whether the motion starts with x=x0sin(ωt) or x=x0cos(ωt)) impacts the graph. It presents graphs of x vs t for two periods, under all four damping scenarios.
• Accessibility: The simulation is designed to be highly accessible, being embeddable in webpages and compatible with various operating systems and devices, emphasizing its suitability for diverse educational settings.

3. Key Ideas and Facts:

• Practical Relevance: The simulation highlights that in real-world scenarios, ideal, undamped oscillations are impossible due to friction.
• Visual Learning: The applet's strength lies in its visual representation of how damping affects oscillatory behavior. Users can see the differences in oscillation decay for various damping levels.
• Exponential Decay in Light Damping: The resource points out that in light damping scenarios, the amplitude of oscillation decays exponentially with time. This is an important detail in understanding the nature of damped motion.
• Critical Damping as Optimization: The concept of critical damping highlights that it's the fastest path for a system to return to equilibrium without overshooting.
• EJS as Simulation Tool: The document also functions as an example of the capabilities of Easy JavaScript Simulation (EJS) for creating interactive educational resources.
• Open Educational Resource: The resource is made available under a Creative Commons license, emphasizing its commitment to open educational practices and allowing free use, modification, and sharing for non-commercial purposes.
• Versatile Educational Tool: The applet can be used across multiple levels including Junior College, and it is a suitable learning tool for physics.

4. Quotes & Supporting Evidence:

• On Damping: "If no frictional forces act on an oscillator... then it will oscillate indefinitely. In practice, the amplitude of the oscillations decreases to zero as a result of friction. This type of motion is called damped harmonic motion."
• On No Damping (b=0.0): "system oscillates forever without coming to rest. Amplitude and thus total energy is constant"
• On Light Damping (b=0.1): "system undergoes several oscillations of decreasing amplitude before coming to rest. Amplitude of oscillation decays exponentially with time."
• On Critical Damping (b=2.0): "system returns to equilibrium in the minimum time, without overshooting or oscillating about the equilibrium position amplitude."
• On Heavy Damping (b=5.0): "system returns to equilibrium very slowly without any oscillation."

5. Additional Context & Links:

• Website: The resource is part of a broader collection hosted at iwant2study.org under "Open Educational Resources / Open Source Physics @ Singapore."
• Simulation Link: http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM20/SHM20_Simulation.xhtml is the direct link to the simulation.
• App Link: https://play.google.com/store/apps/details?id=com.ionicframework.shm20app163344&hl=en The simulation is also available as a mobile app.
• Developer: The simulations are credited to "lookang."

6. Implications & Potential Use:

• Educational Impact: This simulation can be a highly effective tool in the classroom for teaching and visualizing the concept of damped harmonic motion.
• Hands-on Learning: Students can interact with the simulation, varying parameters, and directly observe their effects, enhancing engagement and understanding.
• Resource Development: The document showcases how teachers can utilize EJS to create custom learning resources.

7. Conclusion:

The "10.6 Degrees of Damping HTML5 Applet Simulation Model" is a well-designed and valuable educational tool for teaching the principles of damped harmonic motion. Its interactive nature, accessibility across platforms, and clear demonstration of various damping scenarios make it a significant asset for physics education. The use of EJS to create such interactive content also highlights the potential for further development of similar open educational resources.

Damped Harmonic Motion Study Guide

Quiz

1. What is damped harmonic motion and what causes it? Damped harmonic motion is when an oscillator's amplitude decreases over time due to friction from air resistance or internal forces, causing the oscillations to eventually cease.
2. Describe the behavior of a system with no damping. When there is no damping (b=0.0), the system will oscillate indefinitely without the amplitude decreasing or the motion coming to a rest, thus the total energy of the system is constant.
3. What characterizes a system with light damping? A lightly damped system (b=0.1) will exhibit several oscillations, but with a steadily decaying amplitude over time. The amplitude of oscillation decreases exponentially with time.
4. How does critical damping differ from light damping? Critical damping (b=2.0) returns a system to its equilibrium point in the shortest time possible, without any overshooting or oscillations around the equilibrium position, whereas light damping involves some decaying oscillations.
5. How does heavy damping affect a system's return to equilibrium? A heavily damped system (b=5.0) returns to equilibrium very slowly, without any oscillation. The damping is so large that the system does not oscillate at all and is highly inefficient at returning to the equilibrium position.
6. What is meant by "amplitude" in the context of harmonic motion? Amplitude refers to the maximum displacement of the oscillator from its equilibrium position. It’s the measure of how far the oscillator moves in either direction from its center.
7. What is the significance of the parameter "b" in the provided source material? The parameter "b" represents the damping coefficient, which indicates the level of damping within the system. It determines whether the system has no, light, critical, or heavy damping.
8. What is the difference between x= x0 sin(ωt) and x= x0 cos(ωt) graphs? The x= x0 sin(ωt) graph begins at the equilibrium position and starts at zero displacement, while the x= x0 cos(ωt) graph starts at the maximum displacement (amplitude) from the equilibrium position. Both represent the motion of an oscillator but differ based on the starting position at t=0
9. What are some real-world examples of damped harmonic motion? Real-world examples include the slowing down of a swinging pendulum, a car's shock absorbers reducing bounces after hitting a bump, and the decaying oscillations in a guitar string after it is plucked.
10. How does the damping in a system affect the total energy of the system? The total energy of a damped system decreases over time as kinetic energy is dissipated into the environment due to frictional forces. In an undamped system, total energy remains constant.

Answer Key

1. Damped harmonic motion is when an oscillator's amplitude decreases over time due to friction from air resistance or internal forces, causing the oscillations to eventually cease.
2. When there is no damping (b=0.0), the system will oscillate indefinitely without the amplitude decreasing or the motion coming to a rest, thus the total energy of the system is constant.
3. A lightly damped system (b=0.1) will exhibit several oscillations, but with a steadily decaying amplitude over time. The amplitude of oscillation decreases exponentially with time.
4. Critical damping (b=2.0) returns a system to its equilibrium point in the shortest time possible, without any overshooting or oscillations around the equilibrium position, whereas light damping involves some decaying oscillations.
5. A heavily damped system (b=5.0) returns to equilibrium very slowly, without any oscillation. The damping is so large that the system does not oscillate at all and is highly inefficient at returning to the equilibrium position.
6. Amplitude refers to the maximum displacement of the oscillator from its equilibrium position. It’s the measure of how far the oscillator moves in either direction from its center.
7. The parameter "b" represents the damping coefficient, which indicates the level of damping within the system. It determines whether the system has no, light, critical, or heavy damping.
8. The x= x0 sin(ωt) graph begins at the equilibrium position and starts at zero displacement, while the x= x0 cos(ωt) graph starts at the maximum displacement (amplitude) from the equilibrium position. Both represent the motion of an oscillator but differ based on the starting position at t=0
9. Real-world examples include the slowing down of a swinging pendulum, a car's shock absorbers reducing bounces after hitting a bump, and the decaying oscillations in a guitar string after it is plucked.
10. The total energy of a damped system decreases over time as kinetic energy is dissipated into the environment due to frictional forces. In an undamped system, total energy remains constant.

Essay Questions

1. Compare and contrast the effects of light damping, critical damping, and heavy damping on the motion of a harmonic oscillator. Use examples to illustrate each type of damping in real-world applications.
2. Discuss how damping affects the energy of a harmonic oscillator over time, explaining why energy is conserved in ideal (undamped) systems and how this relates to real-world examples.
3. Analyze how the starting position of a harmonic oscillator, described by x= x0 sin(ωt) and x= x0 cos(ωt), influences the subsequent motion of the system, considering both the absence and presence of damping.
4. The simulation model uses ‘b’ as a damping coefficient, explain how and why this value is used in simulations to describe the physical characteristics of a real world system? How might such a simulation be used in education?
5. Describe the significance of the various types of damping in practical applications (e.g., in engineering, music, or other scientific fields). How do engineers and scientists use these principles to control and mitigate the effects of oscillations?

Glossary of Key Terms

• Harmonic Motion: Motion that repeats itself in equal intervals of time, characterized by a back-and-forth movement about an equilibrium position.
• Damped Harmonic Motion: Harmonic motion where the amplitude of the oscillations decreases over time due to energy dissipation through friction or other resistive forces.
• Oscillator: A system that exhibits repetitive motion, such as a mass on a spring or a pendulum.
• Amplitude: The maximum displacement of an oscillator from its equilibrium position.
• Damping: The process where energy is removed from an oscillating system, causing the amplitude to decrease over time.
• Friction: A force that opposes motion between surfaces in contact or within a fluid, resulting in the dissipation of energy.
• Equilibrium Position: The position of an oscillator where there is no net force acting on it, causing it to be at rest.
• Damping Coefficient (b): A parameter that quantifies the amount of damping in a system, where higher values indicate stronger damping.
• Light Damping: A type of damping where the system undergoes several oscillations of decreasing amplitude before coming to rest.
• Critical Damping: A type of damping where the system returns to equilibrium in the shortest time possible, without overshooting or oscillating.
• Heavy Damping: A type of damping where the system returns to equilibrium very slowly, without oscillation.
• Exponential Decay: A decrease in a quantity over time at a rate proportional to its current value, often observed in damped oscillations.
• ω (Omega): Represents the angular frequency of oscillation, determining the speed of the oscillations, not the amplitude.

Apps

https://play.google.com/store/apps/details?id=com.ionicframework.shm20app163344&hl=en

FAQ: Damped Harmonic Motion and Interactive Simulations

• What is damped harmonic motion and how does it differ from simple harmonic motion?
• Damped harmonic motion describes the oscillatory movement of a system where the amplitude of oscillations decreases over time due to frictional forces. In contrast, simple harmonic motion (SHM) refers to an ideal scenario where oscillations continue indefinitely with a constant amplitude because there's no energy loss through friction. In real-world systems, damping is almost always present.
• What causes damping in an oscillating system?
• Damping is caused by frictional forces that dissipate energy from the oscillating system, leading to a reduction in the amplitude of the oscillations. These forces can arise from air resistance, internal friction within the system, or other external factors that impede motion.
• How does the damping coefficient (represented by 'b') affect the behavior of a damped oscillator?
• The damping coefficient (b) determines the rate at which the oscillations decrease. A small value for 'b' indicates light damping, where the system will oscillate several times before coming to rest. A larger 'b' signifies heavier damping, where the system returns to equilibrium slowly without oscillation. Critical damping, with a specific 'b' value (e.g. b=2.0 in the simulation), causes the system to return to equilibrium in the minimum time, without oscillating or overshooting.
• What are the different types of damping illustrated in the simulation model?
• The simulation model illustrates four different damping conditions: no damping (b=0.0), light damping (e.g., b=0.1), critical damping (e.g., b=2.0), and heavy damping (e.g., b=5.0). These conditions are visually represented by x vs t graphs, showing how the amplitude of the oscillations or return to equilibrium is affected by varying values of 'b'.
• How does the simulation model help in understanding damped harmonic motion?
• The simulation model allows users to visualize and interact with the concepts of damped harmonic motion. By changing the damping coefficient (b), users can observe how the system's behavior changes, ranging from continuous oscillations to a slow, non-oscillatory return to equilibrium. This hands-on approach provides a more intuitive grasp of the underlying physical principles.
• Are there other simulations and learning resources available on the website beyond damped harmonic motion?
• Yes, the website hosts a wide range of interactive physics simulations and resources, covering various topics including Newtonian mechanics, oscillations, gravitational fields, electromagnetism, wave phenomena, collisions, optics, and more. These resources are designed for different educational levels, from primary school to junior college.
• What are some of the tools used to create these interactive simulations?
• The simulations are created using Easy JavaScript Simulation (EJS) authoring toolkit and are compatible with multiple platforms, including web browsers, Android, and iOS devices. The site also uses WebGL for 3D visualizations. This flexibility allows for a broader audience to access and utilize the resources for educational purposes.
• What is the licensing of the material on the website? The content is licensed under a Creative Commons Attribution-Share Alike 4.0 Singapore License. For commercial use of the EasyJavaScriptSimulations library, it's necessary to contact This email address is being protected from spambots. You need JavaScript enabled to view it. directly and adhere to the terms outlined in the specified EJS license.