About

1.2.4 Acceleration

 

From v = v_o cos ω t = x₀ ω cos ω t

where x_o is the maximum displacement

differentiating we get

 $$a=\frac{dv}{dt}=-<!--\; -\; -->{\omega }^2(x_{0}sin\omega t)=-<!--\; -\; -->{\omega }^{2}x$$
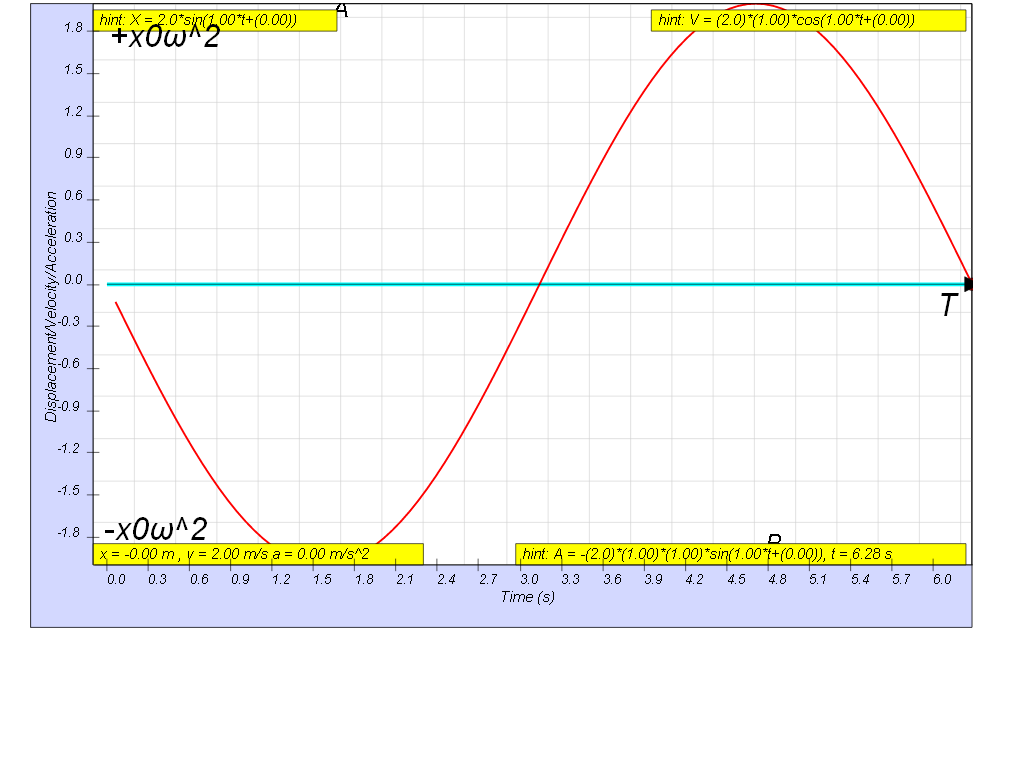
  Variation with time of acceleration   

In terms of x:

 
Therefore,  a = - xo ω² sin ω t
                   = - ω² (x_o sin ω t)
which is the defining equation for S.H.M. !
               a     = - ω² x
 
 
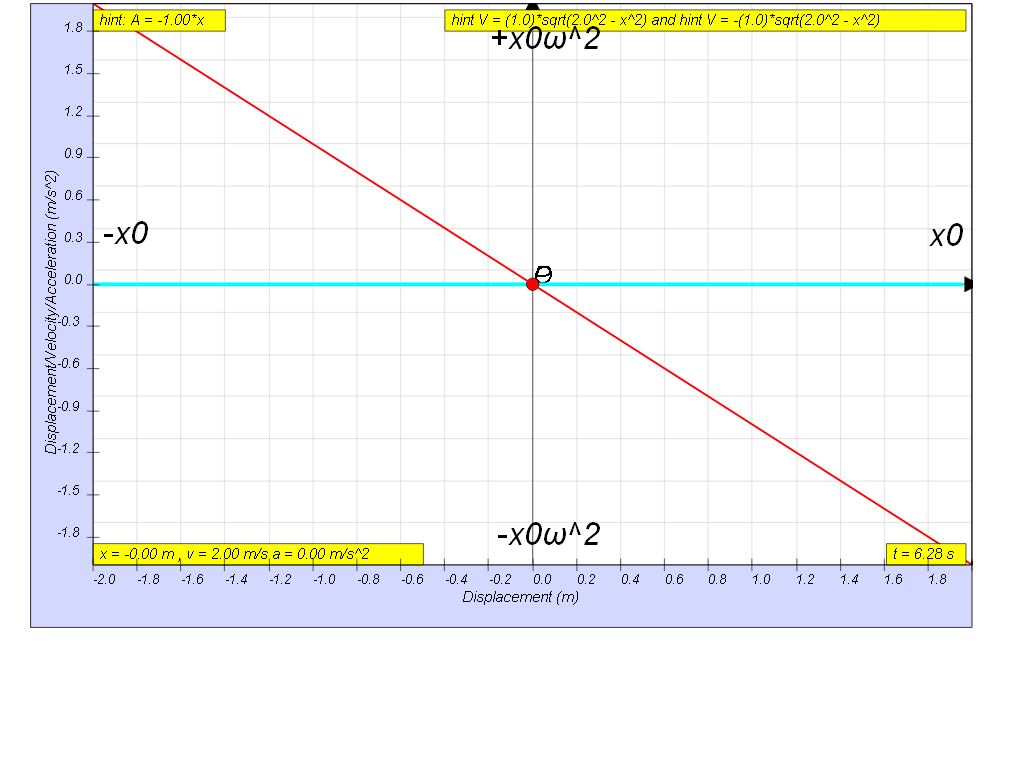
Variation with displacement of acceleration 

since 
   
        a = – a₀sin ω t         

where a_o is the maximum acceleration
where by a₀ = ω² (x_o)  

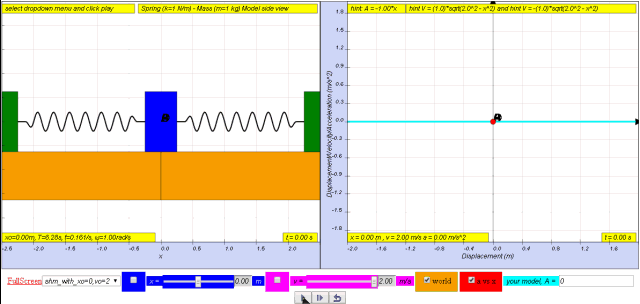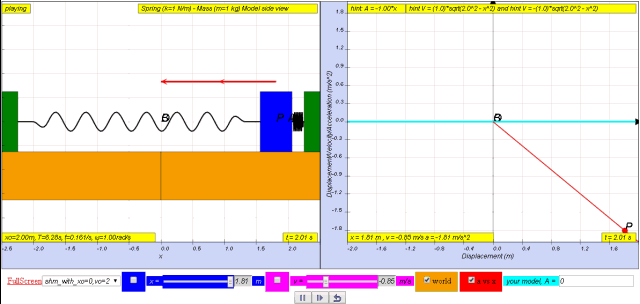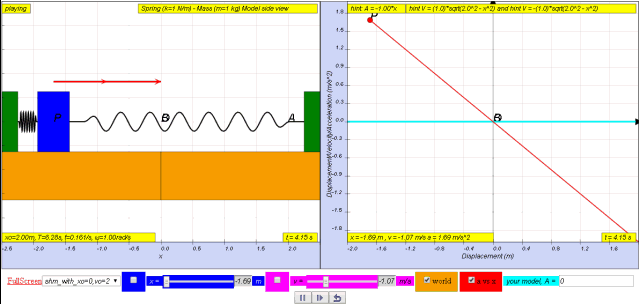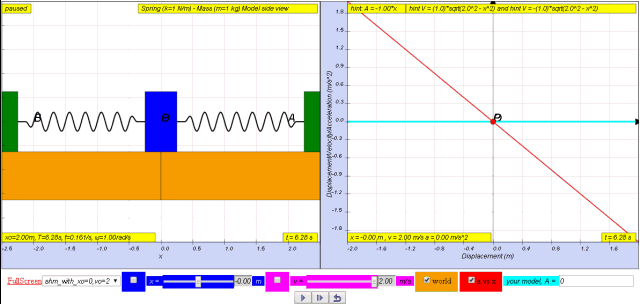
1.2.3.1 Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/74

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM10/SHM10_Simulation.xhtml

Briefing Document: ⚛️ Horizontal Spring Mass Model Simulation

Date: October 26, 2024 Subject: Analysis of "10.2.4 Horizontal Spring Mass Model Acceleration versus Position JavaScript HTML5 Applet Simulation Model"

1. Introduction:

This document provides a summary of the web page describing an interactive simulation of a horizontal spring-mass system, developed by the Open Educational Resources / Open Source Physics @ Singapore project. The primary focus is on the relationship between acceleration and displacement in simple harmonic motion (SHM), a core concept in introductory physics. The simulation is designed as a learning tool accessible across multiple platforms.

2. Key Themes and Concepts:

• Simple Harmonic Motion (SHM): The core concept is SHM, specifically, the oscillatory motion of a mass attached to a spring. The simulation allows users to visualize and explore the relationship between a mass's position, velocity, and acceleration as it oscillates.
• Acceleration and Displacement: The primary focus of this specific model is the relationship between the acceleration of the mass and its displacement from the equilibrium position. The key mathematical takeaway is the defining equation for SHM: a = - ω²x .
• Angular Frequency (ω): The equation incorporates ω (angular frequency), which is intrinsic to the SHM and is related to the period and frequency of the oscillation.
• JavaScript HTML5 Applet: The simulation is built as a JavaScript HTML5 applet, making it accessible on a wide range of devices including desktops, laptops, tablets, and smartphones. This makes the resource very versatile for use in different learning environments.
• Open Educational Resource: The project emphasizes open educational resources, and the simulation is meant to be embedded into web pages easily and is available for free.

3. Important Ideas and Facts:

• Derivation of Acceleration: The page explicitly demonstrates how the acceleration equation is derived from the velocity equation. It starts with the velocity equation v = vo cos ω t = x0 ω cos ω t and using differential calculus we arrive at the acceleration equation.
• "Variation with displacement of acceleration since a = – a0sin ω t where ao is the maximum acceleration". This clarifies the nature of the relationship between acceleration and time but also acceleration and position, which is that they have a sinusoidal relationship to each other.
• Defining Equation for SHM: The page clearly states that the derived relationship "a = - ω² x" is the defining equation for Simple Harmonic Motion. This helps learners understand the core concept in the context of this particular physical system.
• Interactivity: The simulation is embeddable via an iframe, meaning it's designed for use as an interactive component in online learning materials. The fact that it is part of a suite of simulations is also important, and is captured by the breadcrumb hierarchy on the page.
• Accessibility: The app is available on multiple operating systems such as Android/iOS, Windows/MacOSX/Linux, and ChromeBook Laptops.
• Additional Resources: The page links to other related simulations, such as those examining velocity vs. position, the defining equation of SHM vs time, and position vs time for the horizontal spring mass model, as well as a simulation on the pendulum. This emphasizes a collection of resources designed to promote deep understanding of oscillatory motion.

4. Key Quotes from the Source:

• "From v = vo cos ω t = x0 ω cos ω t...differentiating we get a = d v/ d t = - ω² ( x 0 s i n ω t ) = - ω² x " This shows the explicit derivation of the acceleration equation.
• "Therefore, a = - xo ω2 sin ω t = - ω2 (xo sin ω t) which is the defining equation for S.H.M." This statement explicitly identifies the derived equation with the definition of SHM
• "Variation with displacement of acceleration since a = – a0sin ω t where ao is the maximum acceleration" which clarifies the sinusoidal relationship between acceleration and position (or time)

5. Educational Implications:

• Conceptual Understanding: The simulation aids in visualizing abstract concepts, allowing learners to "see" the relationship between acceleration and position in SHM.
• Active Learning: The interactive nature of the applet encourages learners to explore the model and test their understanding.
• Accessibility and Flexibility: The platform-agnostic design makes the resource suitable for diverse learning environments.
• Supplement to Lectures: It can be used as a supplemental tool in lectures or as an assignment to be completed individually by students, fostering a deeper understanding of the subject matter.

6. Conclusion:

The "10.2.4 Horizontal Spring Mass Model Acceleration versus Position JavaScript HTML5 Applet Simulation Model" provides a valuable educational resource for understanding the core principles of Simple Harmonic Motion. Its interactive nature, combined with the explicit mathematical relationships, makes it an excellent tool for learners at the Junior College level and above. It also provides evidence of a more comprehensive learning environment, as evidenced by the long list of supporting simulation models, which suggests a coordinated approach to teaching physics concepts via modeling.

Simple Harmonic Motion: Horizontal Spring-Mass Model Study Guide

Quiz

Instructions: Answer the following questions in 2-3 sentences each.

1. What is the relationship between acceleration and displacement in simple harmonic motion (SHM)?
2. In the horizontal spring-mass model, what does the variable 'x0' represent?
3. What mathematical relationship defines Simple Harmonic Motion and how does this relate to the motion of the spring-mass model described in the text?
4. What does the term ω (omega) represent in the context of the equations presented?
5. How does acceleration vary with time in SHM?
6. The text provides a formula for 'a'. Identify this formula and explain what it means in terms of the motion of a spring-mass system.
7. What is the significance of the negative sign in the equation a = -ω²x ?
8. If the mass in the simulation were doubled, how would it impact the acceleration, assuming the spring constant is unchanged?
9. According to the document, where can the simulation be embedded?
10. What is the role of JavaScript in the simulations discussed?

Quiz Answer Key

1. In simple harmonic motion (SHM), acceleration is directly proportional to the displacement from the equilibrium position, but acts in the opposite direction. This means the further the mass is from equilibrium, the stronger the restoring force and the greater the acceleration toward equilibrium.
2. In the horizontal spring-mass model, 'x0' represents the maximum displacement of the mass from its equilibrium position. This is also known as the amplitude of the oscillation.
3. SHM is defined by the equation a = -ω²x, where acceleration is proportional to displacement and directed oppositely. The spring-mass model exhibits this relationship, as the restoring force of the spring results in acceleration towards the equilibrium point, which is proportional to how far the spring is stretched or compressed.
4. The term ω (omega) represents the angular frequency of the oscillation. It determines the rate at which the system completes cycles of motion, and is related to the spring constant and mass.
5. Acceleration varies sinusoidally with time in SHM, following a negative sine wave as a = -a0 sin(ωt) where a0 is the maximum acceleration. It reaches a maximum when velocity and displacement are zero and is zero when velocity is maximum and acceleration is at equilibrium.
6. The formula a = -ω²x means that acceleration (a) is proportional to the negative of the displacement (x) multiplied by the square of angular frequency (ω²). This relationship shows that acceleration is greatest when displacement is maximal and zero when displacement is zero.
7. The negative sign in a = -ω²x indicates that the acceleration is always directed opposite to the displacement. This is the nature of a restoring force, as it pushes the mass back towards the equilibrium position.
8. If the mass in the simulation were doubled, and the spring constant is unchanged, the frequency and therefore also the angular velocity would be lower, resulting in lower acceleration. The relationship between mass (m) and angular frequency (ω) is ω=sqrt(k/m) where k is spring constant and m is mass.
9. The simulation can be embedded in webpages using an iframe, as noted in the text. This functionality allows for easy integration into online educational materials.
10. JavaScript is used to create interactive HTML5 applet simulations, allowing for dynamic manipulation and visual representation of the spring-mass model. This makes the simulation functional on various platforms.

Essay Questions

Instructions: Answer each of the following questions in a well-organized essay format with supporting information from the provided documents.

1. Explain how the relationship between acceleration and displacement demonstrates that the horizontal spring-mass model exhibits Simple Harmonic Motion, providing detail about the mathematical representation of this relationship.
2. Describe the energy transformations that occur during one complete oscillation of the horizontal spring-mass system. Include how the simulation could visually represent these transformations.
3. Discuss the significance of angular frequency (ω) and how changing the parameters of the spring or mass would affect the angular frequency and resulting SHM, explaining the connection to the formula provided.
4. Analyze the ways in which the provided web-based interactive simulation tools could enhance student understanding of abstract concepts in physics, considering specific features of the simulation and how these might address student misunderstandings.
5. Based on the provided text, explain how the concept of simple harmonic motion extends beyond the horizontal spring-mass model, referencing other models or simulations mentioned in the text as examples of oscillatory behavior.

Glossary of Key Terms

Simple Harmonic Motion (SHM): A type of periodic motion where the restoring force is directly proportional to the displacement and acts in the opposite direction. Characterized by a sinusoidal motion pattern.

Displacement (x): The distance of an object from its equilibrium position. Can be positive or negative depending on direction.

Acceleration (a): The rate at which the velocity of an object changes over time. In SHM, it is proportional to displacement.

Angular Frequency (ω): A measure of how rapidly an oscillation occurs, measured in radians per second. It is related to the frequency (f) of oscillation by ω = 2πf.

Maximum Displacement (x0): The largest distance an oscillating object moves away from its equilibrium position, also called the amplitude of the motion.

Restoring Force: A force that acts to bring an object back to its equilibrium position. In the spring-mass model, this force is provided by the spring.

Equilibrium Position: The position where the net force on an object is zero, causing no acceleration. In the spring-mass model, it's the relaxed length of the spring.

HTML5 Applet: A small application or program that can be embedded within a webpage, often used for interactive simulations and educational tools.

JavaScript: A programming language commonly used to add interactivity to websites, often used to control applets.

Iframe: HTML element used to embed another HTML document within the current document. In the given context, it is used to embed the simulation in a webpage.

Video

https://notebooklm.google.com/notebook/d918b9a7-4652-407b-b140-1d17a9f3641d/audio

FAQ

• What is Simple Harmonic Motion (SHM) and how does the horizontal spring-mass model demonstrate it?
• Simple Harmonic Motion is a type of periodic motion where the restoring force is directly proportional to the displacement and acts in the opposite direction. In a horizontal spring-mass system, when the mass is displaced from its equilibrium position, the spring exerts a restoring force that pulls or pushes the mass back towards equilibrium. This results in the mass oscillating back and forth, exhibiting SHM. The key characteristic is that the acceleration is always proportional and opposite to the displacement, described by the equation a = -ω²x.
• How is acceleration related to displacement in SHM?
• In Simple Harmonic Motion, the acceleration (a) is directly proportional to the displacement (x) but in the opposite direction. This relationship is expressed by the equation a = -ω²x, where ω (omega) represents the angular frequency. The negative sign indicates that the acceleration always acts towards the equilibrium point, while the magnitude of the acceleration is proportional to the magnitude of the displacement. This relationship is fundamental to defining SHM.
• What is the significance of ω (omega) in the SHM equation?
• In the equation a = -ω²x, ω (omega) represents the angular frequency of the oscillation. Angular frequency is a measure of how rapidly the oscillation is occurring and is related to the period (T) and frequency (f) of the SHM by the equations ω = 2π/T and ω = 2πf. A higher ω indicates a faster oscillation. This term is crucial in determining the acceleration at any given displacement in SHM.
• What are the key parameters that affect the behavior of the spring-mass system in SHM simulations?
• The main parameters that affect the behavior of the spring-mass system include: the mass (m) of the object, the spring constant (k) which reflects the stiffness of the spring, the initial displacement (x₀), and initial velocity (v₀) of the mass. These values collectively determine the period, frequency, amplitude, and energy of the oscillation. For example, a higher spring constant results in faster oscillations while a larger mass leads to slower oscillations. These can be adjusted in simulations to see their effects.
• What kinds of educational resources are offered on the Open Educational Resources / Open Source Physics @ Singapore platform? The platform offers a wide variety of interactive simulations and models related to physics and other STEM fields. These range from basic mechanics concepts such as oscillations, Newtonian mechanics, and projectile motion, to more complex topics like electromagnetism, optics, thermodynamics, and quantum mechanics. The resources are primarily designed for secondary and tertiary education and are designed using the Easy JavaScript Simulation (EJS) authoring toolkit. There are also projects covering math and chemistry education.
• What is the purpose of the JavaScript HTML5 applets provided by the platform?
• The JavaScript HTML5 applets are interactive simulations designed to enhance understanding of physics and STEM concepts through visualization and experimentation. They allow users to manipulate variables, such as mass, spring constant, or initial velocity, and observe the resulting changes in system behavior in real time. The applets are designed to be accessible on a variety of devices including desktops, laptops, and mobile devices. This allows for greater exploration and experiential learning.
• What is the license associated with the content on this site?
• The content on the Open Educational Resources / Open Source Physics @ Singapore platform is licensed under the Creative Commons Attribution-Share Alike 4.0 Singapore License. This means the content can be freely shared, adapted, and used for both educational and commercial purposes as long as appropriate credit is given and the work is shared under the same licensing terms. However, commercial use of the underlying EasyJavaScriptSimulations Library requires separate licensing arrangements with the University of Murcia (contact This email address is being protected from spambots. You need JavaScript enabled to view it.).
• How can users access and utilize the resources available on this platform?
• The resources are typically embedded within web pages using iframes. Users can access the interactive simulations by visiting the provided links, many of which directly lead to a webpage with the embedded interactive simulation. Additionally, many resources are listed by project name or specific topic, making them readily searchable via the website. Educators can integrate these resources into their curriculum, and students can use them for self-guided learning and exploration of physical principles.