About

1.2.5 Example

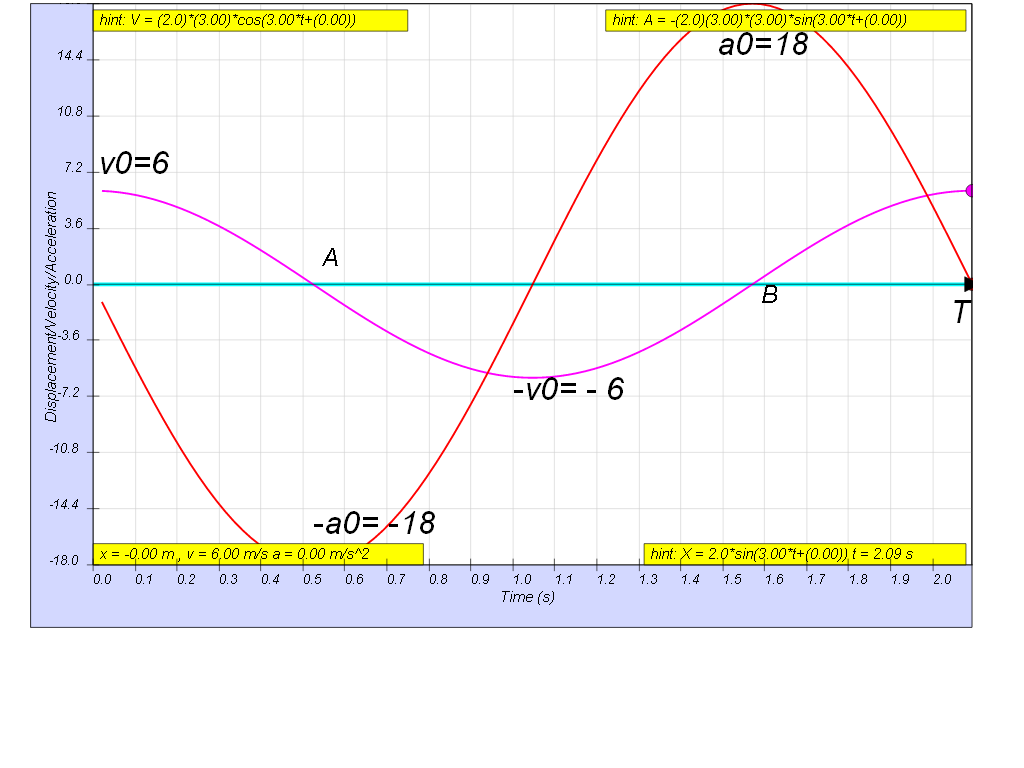
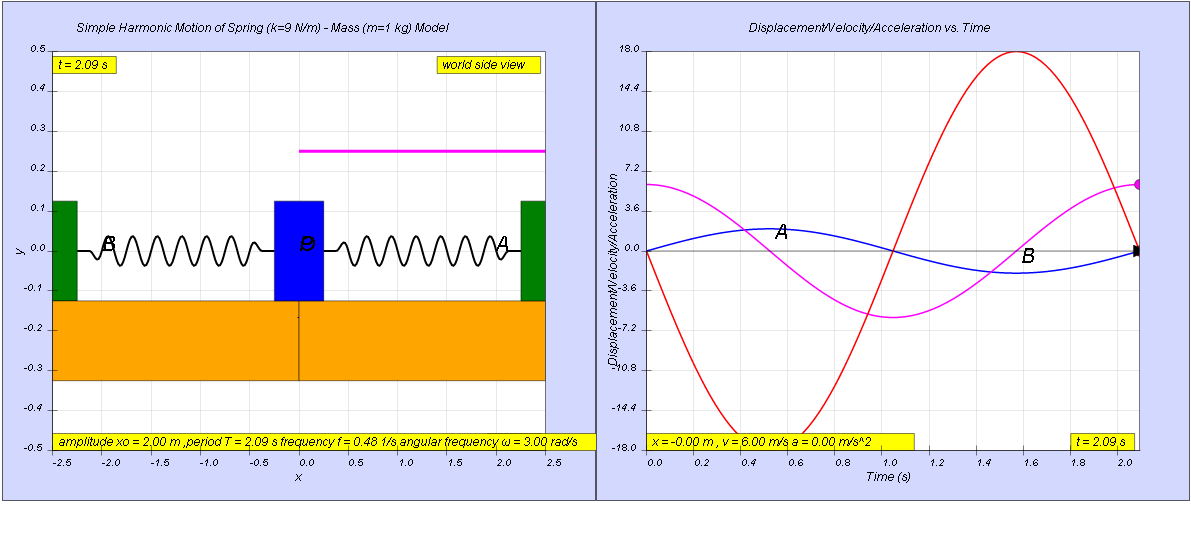
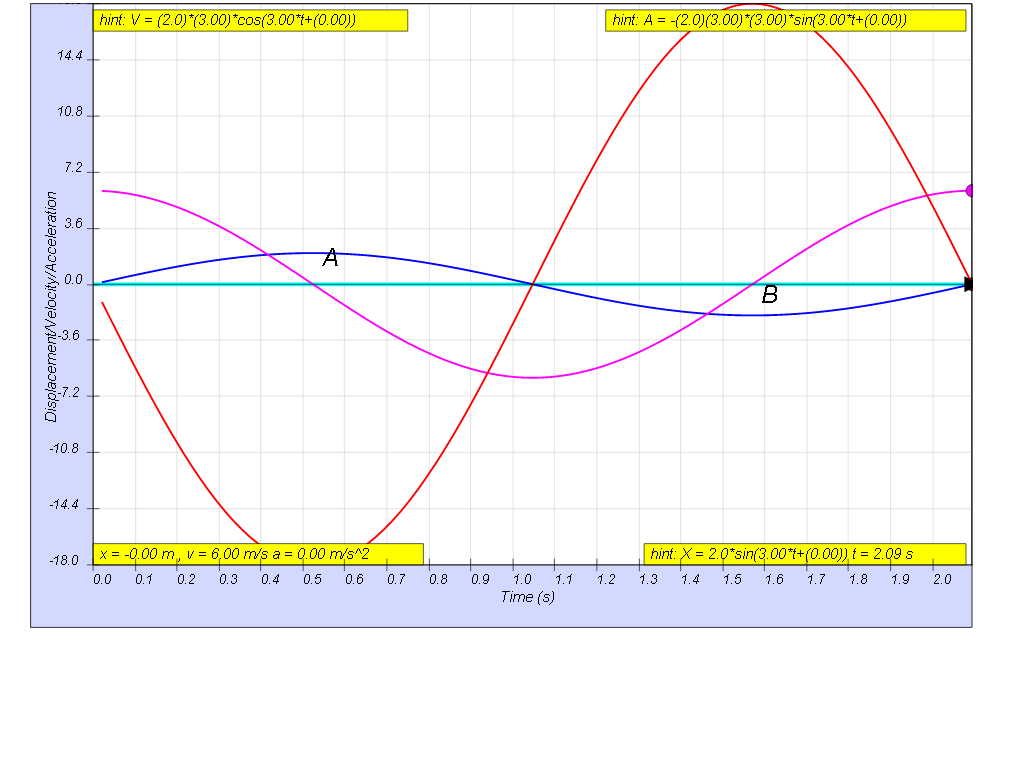
The graphs show how the variation with time of the velocity, v and the acceleration, a of a body when it is oscillating with simple harmonic motion.
(a)    Determine the period, T.
(b)    Sketch the variation with time of the displacement, x, of the oscillating body
[ 2.09 s, x = 2  sin( 3t )]

1.2.5.1 Solution:

a) maximum velocity , v₀ = x₀ω = 6 m/s

maximum acceleration a₀ = x₀ω² = 18 m/s²

thus dividing the 2 equations, we get ω = 3 rad/s

therefore since $\omega =\genfrac{}{}{0.1ex}{}{2\pi }{T}$

using the model to test check out your answer!

1.2.5.2 Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/73

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM11/SHM11_Simulation.xhtml

Briefing Document: ⚛️Spring-Mass Model Simulation (SHM11)

Source: Excerpts from "10.2.5 Example Spring (k=9 N/m) - Mass (m=1 kg) model x0=0, v0 =6 Position versus time JavaScript HTML5 Applet Simulation Model - Open Educational Resources / Open Source Physics @ Singapore"

Date: Information extracted in October 2024 (as determined by the source title which includes "2024")

Overview:

This document analyzes a specific example within a larger collection of physics simulations focusing on simple harmonic motion (SHM). The example, designated as "10.2.5," presents a spring-mass system with defined parameters (spring constant k = 9 N/m, mass m = 1 kg) and initial conditions (initial position x0=0, initial velocity v0 = 6 m/s). The provided material includes a brief description of the model, a sample problem related to the simulation, its solution, and links to run the simulation. It also notes the platform compatibility and licensing details.

Key Themes and Concepts:

1. Simple Harmonic Motion (SHM): The core focus is on demonstrating and analyzing SHM, specifically the oscillations of a mass attached to a spring. The simulation allows users to visualize the relationship between position, velocity, and acceleration over time in a SHM system.
2. Mathematical Relationships: The document demonstrates the mathematical formulas underlying SHM. It shows how to calculate the period (T) of oscillation from the angular frequency (ω), which is found by analyzing the maximum velocity and acceleration. Specifically:

• The maximum velocity (v0) is related to the initial displacement (x0) and angular frequency (ω) by the equation v0 = x0ω.
• The maximum acceleration (a0) is related to the initial displacement (x0) and angular frequency (ω) by the equation a0 = x0ω².
• The angular frequency (ω) is related to the period (T) by the equation ω = 2π/T.

1. Simulation as a Learning Tool: The material highlights the use of an interactive JavaScript HTML5 applet as a tool to visualize and explore abstract physics concepts. The document encourages the user to “use the model to test check out your answer!” implying its function as a testing and verification tool for calculations and intuitions. The embedded iframe also shows the practical use of the simulation model directly.
2. Accessibility and Open Source: The simulation is designed for accessibility across different platforms, including “Android/iOS including handphones/Tablets/iPads” and “Windows/MacOSX/Linux including Laptops/Desktops”. It also highlights its use in ChromeBooks, showcasing a wide compatibility range. The resource is shared under a “Creative Commons Attribution-Share Alike 4.0 Singapore License,” indicating an open-source and shareable nature.

Key Facts and Ideas:

• Model Parameters: The specific spring-mass system under consideration has a spring constant (k) of 9 N/m and a mass (m) of 1 kg. The initial displacement x0 is 0 and initial velocity is 6 m/s.
• Problem Example: The example problem challenges the user to determine the period (T) of the oscillation. The answer provided is 2.09 seconds. It also requires the user to sketch the displacement x(t) as a function of time, with the provided solution x = 2 sin( 3t )
• Calculations: The solution method involves finding the angular frequency (ω) by dividing the maximum acceleration by the maximum velocity (ω = a0/v0), and then using the angular frequency to find the period (T = 2π/ω).
• Amplitude: By finding the initial displacement (x0) with the initial velocity and the angular frequency from the previous calculations, the user is given the amplitude which is equal to 2 meters (m).
• Platform Compatibility: The simulation is accessible on various devices and operating systems.
• Licensing: The resource is available under a Creative Commons license, with additional conditions for commercial use.
• Interactive nature: There is a strong emphasis on interactive simulations with links to "Run Sim" and the ability to embed the model into webpages. This emphasizes the active learning aspect.
• Wider context: The surrounding links to other simulations and projects on the same page demonstrate a large scope of interactive learning tools developed by the same project. Some simulations focus on other aspects of physics (e.g. gravity, escape velocity, electromagnetism, wave mechanics), while others focus on math (e.g. shapes, nets) or even chemistry and geography.

Quotes:

• "The graphs show how the variation with time of the velocity, v and the acceleration, a of a body when it is oscillating with simple harmonic motion." - Describing the intention of the problem example.
• "using the model to test check out your answer!" - Highlighting the interactive nature and use for testing and learning.
• "Open Educational Resources / Open Source Physics @ Singapore" - Indication of the goals and source of the material

Implications:

This resource is valuable for teaching and learning about SHM. The combination of the interactive simulation and the example problem provides a hands-on experience for students to visualize and understand the underlying physics. The open-source nature and accessibility across platforms make it a readily available educational tool for a variety of learning environments.

Further Research:

• Explore the other simulation models linked within the document for more comprehensive understanding of related physics concepts.
• Investigate the EasyJavaScriptSimulation Library mentioned for potential use in developing similar educational resources.
• Review the license agreement to understand specific use and attribution requirements.

This briefing document should provide a comprehensive overview of the key aspects of the provided source.

Simple Harmonic Motion Study Guide

Quiz

Instructions: Answer the following questions in 2-3 sentences each.

1. What is simple harmonic motion (SHM)?
2. In the given simulation, what are the initial conditions for the mass-spring system?
3. What is the maximum velocity (\(v_0\)) of the oscillating mass in the simulation, and what does it represent?
4. What is the maximum acceleration (\(a_0\)) of the oscillating mass, and how is it related to the maximum velocity?
5. What is the angular frequency (ω) of the system, and how is it calculated?
6. What is the period (T) of the oscillation, and how is it related to the angular frequency?
7. What does x₀ represent in the context of the simulation?
8. What is the relationship between displacement (x), velocity (v), and acceleration (a) in SHM?
9. What is the formula for displacement (x) as a function of time (t) in the given simulation?
10. How can you use the provided simulation to verify your answers regarding SHM calculations?

Quiz Answer Key

1. Simple Harmonic Motion (SHM) is a type of periodic motion where the restoring force is directly proportional to the displacement and acts in the opposite direction to that displacement, resulting in oscillations around an equilibrium position. This motion is characterized by a sinusoidal pattern over time.
2. The initial conditions are: the mass of 1 kg is at an initial position of \(x_0 = 0\) and an initial velocity of \(v_0 = 6\) m/s. This means the mass starts at the equilibrium point but already moving.
3. The maximum velocity (\(v_0\)) is 6 m/s and it represents the highest speed the oscillating mass reaches during its motion. It occurs when the mass is passing through the equilibrium position.
4. The maximum acceleration (\(a_0\)) is 18 m/s². It’s related to maximum velocity through the angular frequency: \(a_0 = v_0ω\).
5. The angular frequency (ω) of the system is 3 rad/s. It is found by dividing the maximum acceleration by the maximum velocity (ω = a₀ / v₀), and it represents how fast the object is oscillating.
6. The period (T) of the oscillation is 2.09 s. The relationship between the period and the angular frequency is that ω = 2π / T. The period represents the time it takes for one complete cycle of the oscillation.
7. x₀ represents the amplitude of the oscillation, or the maximum displacement of the mass from its equilibrium position. In this model, it has a value of 2 meters.
8. In SHM, the displacement, velocity, and acceleration are all sinusoidal functions of time and related through derivatives. Velocity is the time derivative of displacement, and acceleration is the time derivative of velocity (and second time derivative of displacement).
9. The displacement (x) as a function of time (t) in this simulation is x = 2 sin(3t). It represents the position of the mass at any given time, as it oscillates back and forth.
10. You can use the simulation to test the values calculated for the period, the displacement as a function of time, maximum acceleration and velocity. Simply running the simulation allows for a visual check of the motion’s characteristics.

Essay Questions

Instructions: Answer the following essay questions in a well-organized format. Provide detailed explanations and support your ideas with evidence from the source material.

1. Discuss the relationship between the maximum velocity, maximum acceleration, and angular frequency in simple harmonic motion (SHM), using the specific example provided in the simulation model. Explain how these parameters are interrelated and what role they play in the system's oscillatory behavior.
2. Explain how the period of an oscillating system is determined and how it is related to the angular frequency of the system. What factors affect the period of an oscillating system, and how would changing these factors impact the oscillations observed?
3. Describe how you can use the simulation model to verify the calculated values for a) the period of the oscillation, b) maximum velocity and c) maximum acceleration. What steps would you take and what would you observe?
4. Discuss the similarities and differences between the displacement, velocity, and acceleration graphs in SHM. How are these three parameters related, and what do these relationships tell us about the oscillating system’s behavior over time?
5. Compare and contrast simple harmonic motion with other types of periodic motion. In what situations is SHM a good model for describing real-world phenomena, and when might it be inadequate?

Glossary

• Simple Harmonic Motion (SHM): A type of periodic motion where the restoring force is directly proportional to the displacement and acts in the opposite direction.
• Period (T): The time taken for one complete cycle of oscillation, measured in seconds.
• Angular Frequency (ω): The rate of change of the phase of an oscillation, measured in radians per second (rad/s). It is related to the frequency and period by ω = 2πf = 2π/T.
• Displacement (x): The distance of an oscillating object from its equilibrium position at any given time.
• Amplitude (x₀): The maximum displacement of an oscillating object from its equilibrium position.
• Maximum Velocity (v₀): The highest speed reached by an object undergoing SHM, which occurs when it passes through the equilibrium position.
• Maximum Acceleration (a₀): The highest magnitude of acceleration in SHM, which occurs at the points of maximum displacement.
• Initial Conditions: The state of a system at the beginning of its motion, including position and velocity.
• Restoring Force: A force that acts to return an object to its equilibrium position.
• Equilibrium Position: The position where the net force on the object is zero.
• Oscillation: The repetitive back-and-forth motion of an object around an equilibrium position.

 

Video

https://notebooklm.google.com/notebook/206bc6f0-5a68-4bd1-aa48-3d7c75fb8921/audio

Frequently Asked Questions

1. What is the main focus of the provided resource?

The primary focus is on demonstrating and simulating simple harmonic motion (SHM) using a spring-mass system. The resource provides a JavaScript HTML5 applet simulation model that allows users to visualize and explore the relationship between position, velocity, and acceleration of an oscillating body. It also includes a solved example to calculate period and displacement, which further reinforces a deeper understanding of the concept. This resource also serves as an example of using the Easy JavaScript Simulation (EJS) tool to create physics simulations.

2. What is the physical system being simulated in the applet?

The applet simulates a mass attached to a spring undergoing simple harmonic motion. The specific example given uses a spring with a spring constant of 9 N/m and a mass of 1 kg. The simulation models the behavior of the system over time, visually showing how the position, velocity, and acceleration of the mass change as it oscillates back and forth. The initial conditions include the mass starting at the equilibrium position with an initial velocity of 6 m/s.

3. How is the period of oscillation calculated in this example?

The period of oscillation (T) is calculated using the relationships between maximum velocity (v₀), maximum acceleration (a₀), and angular frequency (ω). First, v₀ = x₀ω and a₀ = x₀ω² are given, where x₀ is the amplitude. Dividing the two equations, ω = a₀ / v₀, is found. The angular frequency is then used to calculate the period with the formula ω = 2π/T. In the provided example, where v₀ = 6 m/s and a₀ = 18 m/s², the angular frequency (ω) is calculated as 3 rad/s. This leads to a period T of approximately 2.09 seconds.

4. What is the significance of the values v0 = 6 m/s and x0 = 2 m?

v₀ = 6 m/s represents the maximum velocity of the oscillating mass, which occurs as it passes through the equilibrium position. x₀ = 2 m represents the amplitude, or maximum displacement, of the oscillating mass from the equilibrium position. These values, combined with the angular frequency, define the specific oscillatory motion being simulated. The initial velocity is what provides the energy to the system, and x0 represents the extreme positions.

5. What are some of the technologies and tools used to create these educational resources?

The resource utilizes JavaScript and HTML5 to create the applet simulation, ensuring accessibility across various devices, including computers and mobile devices. The resource is also created with the Easy JavaScript Simulation (EJS) tool. EJS appears to be a framework specifically designed for generating interactive simulations. The variety of resources on this page indicate that it is a widely used resource in the Singapore education system.

6. How does this simulation aid in learning about simple harmonic motion?

The simulation provides a visual and interactive way to understand simple harmonic motion, something that can be difficult to conceptualize from equations alone. By running the simulation, students can observe how position, velocity, and acceleration change over time. The graphs provided also illustrate the sinusoidal nature of these quantities in SHM. Students can test their answers and gain hands-on experience with the parameters of the system by manipulating the simulation, strengthening their intuitive understanding.

7. Besides oscillations, what other types of physics simulations are included on the website?

The website provides a wide range of physics simulations and tools, going beyond just oscillations. Some of the topics include Newtonian Mechanics, gravity, energy, waves, electromagnetism, optics, and more. There are resources related to projectile motion, collisions, various types of fields, quantum physics, relativity, thermodynamics, material science, circuits, and much more. This website demonstrates a dedication to supporting interactive learning in various areas of physics.

8. What types of learning goals do these simulations aim to support?

The simulations aim to support various learning goals, including: visualizing abstract concepts, testing and verifying solutions, promoting hands-on exploration, facilitating experimentation, and providing accessible educational resources across devices. They help move from a theoretical understanding towards an applied understanding of physics concepts. The variety of projects also highlight a cross-disciplinary approach, linking learning of math, science, and digital literacy. By making abstract concepts visual, simulations like this aim to create a more intuitive approach to physics.