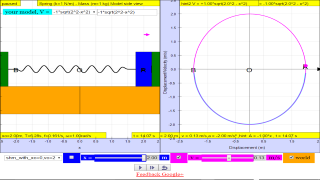
About

1.2.3 Velocity LO (f)

From x = x_o sin ω t 

differentiating we get

where   v₀ = x₀ ω    is the maximum velocity

 
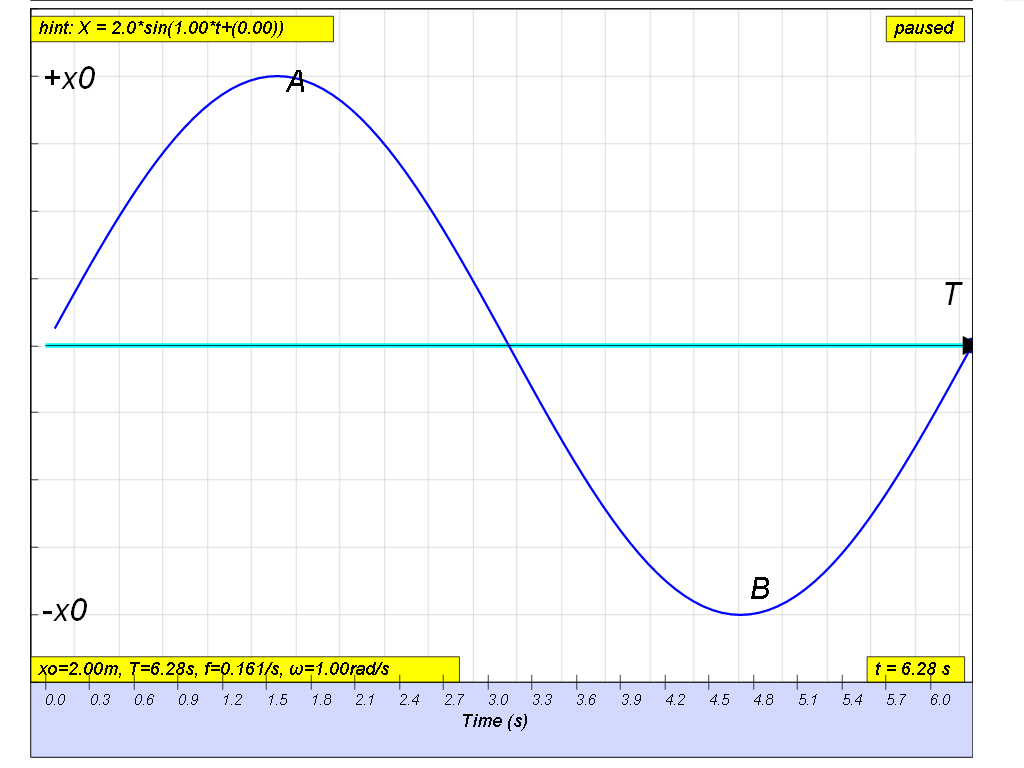
Variation with time of velocity  

In terms of x:

           
From mathematical identity     cos² ωt + sin² ωt = 1,

rearranging

cos² ωt       = 1 - sin² ωt

$$cos\omega t=\pm \sqrt{(1-<!--\; -\; -->si{n}^2\omega t)}$$
     
since

v       =  x₀ω cos ωt

where x₀ is the maximum displacement

$$v=\pm x_0\omega \sqrt{(1-<!--\; -\; -->si{n}^2\omega t)}$$    
 $$v=\pm x_0\omega \sqrt{(1-<!--\; -\; -->(\frac{x}{x_0}{)}^2)}$$$$$$

$$v=\pm \omega \sqrt{({x_0}^2-<!--\; -\; -->x^2)}$$

    

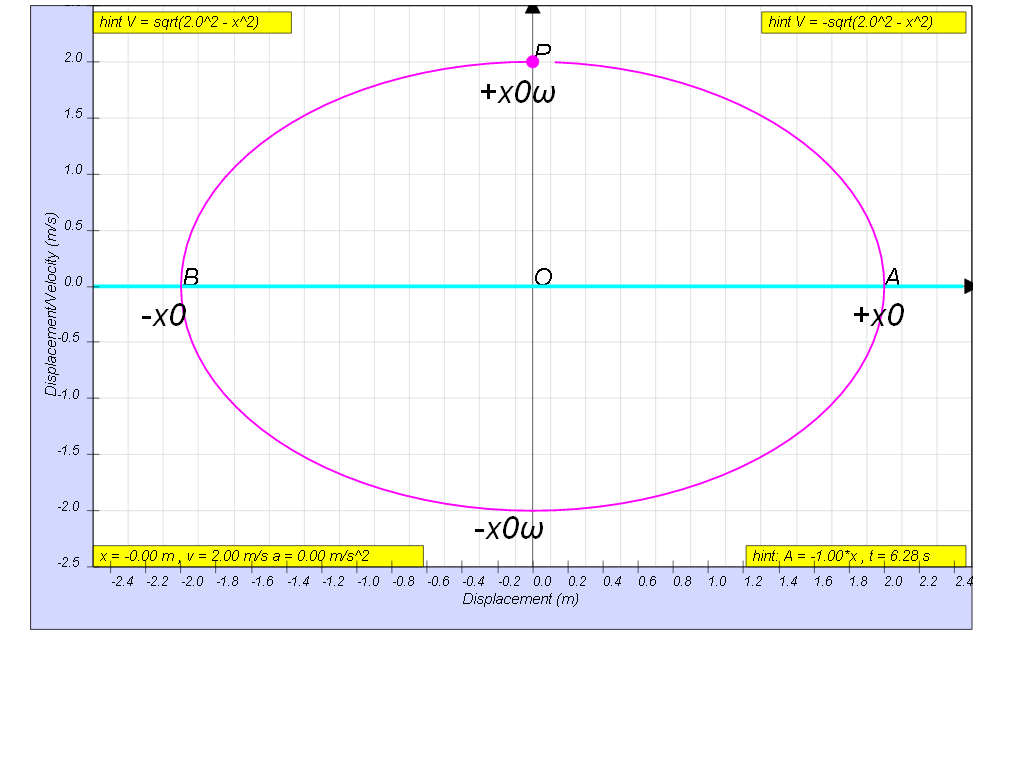
Variation with displacement of velocity

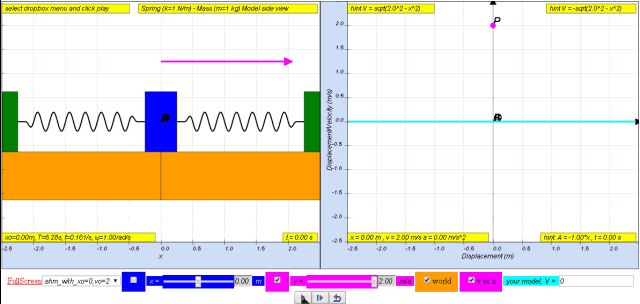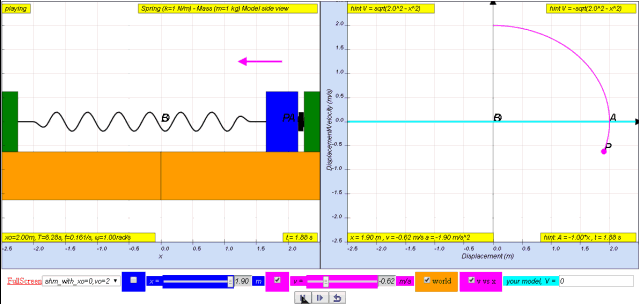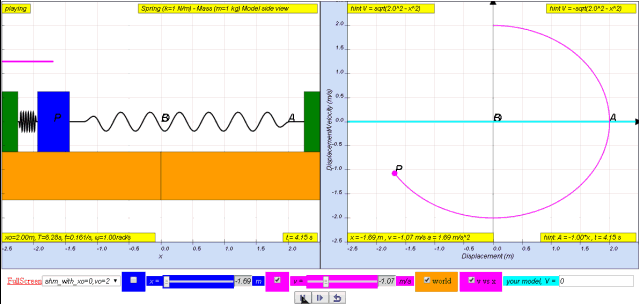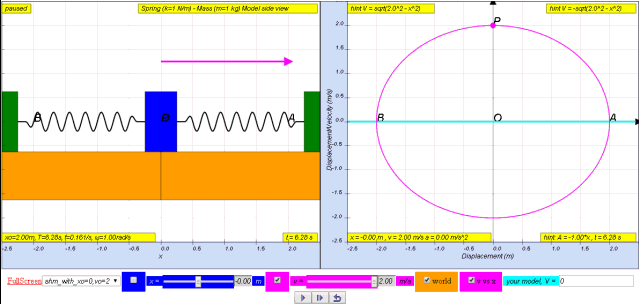
1.2.3.1 Model:

1. Run Sim
2. http://iwant2study.org/ospsg/index.php/72

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM09/SHM09_Simulation.xhtml

Briefing Document: ⚛️Horizontal Spring Mass Model Velocity vs. Position Simulation

1. Overview:

This document analyzes the provided source, which is a webpage from Open Educational Resources / Open Source Physics @ Singapore, focusing on a specific JavaScript HTML5 applet simulation model for a horizontal spring-mass system. The primary focus is on the relationship between velocity and displacement in simple harmonic motion (SHM). The webpage provides access to an interactive simulation and presents the mathematical derivation behind the velocity-displacement relationship. It also highlights the broader ecosystem of educational resources developed using Easy JavaScript Simulation (EJS) and their application across different subjects and grade levels.

2. Key Themes and Concepts:

• Simple Harmonic Motion (SHM): The core of the simulation and the presented mathematics revolves around SHM. This is evident from the title of the model and the equations used to describe the motion. Specifically, the document focuses on the relationship between a mass's velocity and its position (displacement) during oscillation.
• Mathematical Derivation of Velocity-Displacement Relationship: The source provides the step-by-step derivation of the velocity (v) as a function of displacement (x) in SHM.
• It begins with the displacement equation: x = xo sin ω t, where x0 is the maximum displacement and ω is the angular frequency.
• By differentiating the displacement equation with respect to time, the velocity equation is derived: v = x0 ω cos(ωt)
• Using the trigonometric identity cos2 ωt + sin2 ωt = 1, the document proceeds to isolate cos ωt and substitute it back into the velocity equation in terms of displacement x, leading to: v = ± ω ( x 0 2 − x 2 )
• This equation shows that the velocity is maximum at the equilibrium position (x = 0) and is zero at the extreme positions (x = ± x0).
• Interactive Simulation: The webpage embeds an interactive JavaScript applet that allows users to visualize and explore the SHM model. This enhances understanding of the theoretical concepts through practical interaction. The link is included to access the actual simulation.
• Open Educational Resources: The source is part of the Open Educational Resources initiative, aiming to provide free and accessible educational tools. The site hosts many simulations in different areas.
• Easy JavaScript Simulation (EJS): The simulation is created using EJS, which is a tool for developing interactive simulations for educational purposes. Many projects and workshops revolve around this tool, indicating its importance to this group of educators.

3. Important Facts and Ideas:

• Velocity in SHM is NOT Constant: The simulation and derivations emphasize that velocity in SHM is not constant; it varies throughout the motion cycle, being maximum at the equilibrium position and zero at the maximum displacement. The velocity is not directly proportional to displacement, as that would be the case with uniform motion.
• Maximum Velocity: The maximum velocity, v0, is equal to x0 ω.
• Relationship between Velocity and Displacement: The equation v = ± ω ( x 0 2 − x 2 ) demonstrates that the velocity (v) at any displacement (x) depends on the maximum displacement (x0) and angular frequency (ω). The sign ± indicates the direction of the velocity as the mass moves either to the left or right.
• Accessibility: The simulations are designed to be accessible on various devices, including desktops, laptops, tablets, and smartphones.
• Extensive Use of EJS in Education: The webpage is littered with links to simulations made using EJS across multiple disciplines including physics, mathematics, chemistry, geography, and even language education. This shows the widespread use of EJS as a tool for creating engaging and interactive learning experiences.
• Support for Educators: There is a community actively developing resources and conducting workshops to help educators use these tools (many workshops are mentioned, specifically those given by Francisco Esquembre and Félix J. García Clemente.

4. Key Quotes:

• Derivation of Velocity: "From x = xo sin ω t differentiating we get v = d x d t = x 0 ω ( s i n ω t ) = v 0 c o s ( ω t ) where v0 = x0 ω is the maximum velocity"
• Velocity as a function of displacement: "v = ± ω ( x 0 2 − x 2 )"
• About: "SHM09"
• Run Sim: "http://iwant2study.org/ospsg/index.php/72"

5. Implications and Applications:

• Enhanced Conceptual Understanding: The interactive simulation allows students to visualize abstract concepts like SHM and grasp the relationship between displacement and velocity more intuitively.
• Active Learning: The use of simulation encourages active participation in learning, allowing students to explore the concepts independently.
• Versatile Educational Resource: The use of EJS demonstrates a versatile platform for developing interactive educational content, adaptable across various subjects and grade levels, with a large community developing new resources and templates.
• Promotion of Open Educational Resources: This resource promotes the use of freely available educational materials that can be easily shared and adapted by educators worldwide.
• Technology Integration in Teaching: It demonstrates how technology can be integrated into teaching to create engaging and effective learning experiences.

6. Conclusion:

The provided source is a valuable resource for educators teaching physics and related topics, especially concepts related to oscillations and simple harmonic motion. The horizontal spring-mass model simulation provides a clear and interactive way to grasp the core ideas of SHM, specifically the relationship between position and velocity. The extensive use of EJS shows a strong community actively creating open-source educational simulations for students of all ages. The information presented on the webpage is useful to any educator wanting to use interactive simulations in their instruction.

Simple Harmonic Motion: Velocity and Displacement Study Guide

Quiz

Instructions: Answer each question in 2-3 sentences.

1. What is the relationship between velocity and displacement in simple harmonic motion (SHM)?
2. What does x₀ represent in the SHM equations provided?
3. What is the significance of the ± sign in the velocity equation in relation to displacement?
4. How does the maximum velocity (v₀) relate to the angular frequency (ω) and the maximum displacement (x₀)?
5. What mathematical identity is used to derive the velocity equation as a function of displacement?
6. According to the text, what are two ways the velocity of a horizontal spring mass model can be expressed mathematically?
7. What does the provided JavaScript HTML5 applet simulate?
8. Give an example of another model provided in the text that is also an interactive learning tool.
9. What is the purpose of embedding the simulation model into a webpage?
10. Where can the user access the app version of the model?

Quiz Answer Key

1. In SHM, velocity and displacement are not directly proportional but rather, velocity varies with the position of the oscillating mass, reaching its maximum at the equilibrium point and zero at the maximum displacement. The relationship is described by a square root function.
2. x₀ represents the maximum displacement, also known as the amplitude, of the oscillating mass from its equilibrium position. It is the farthest point the mass reaches in its oscillation.
3. The ± sign indicates that the velocity can be either positive or negative depending on the direction of motion of the mass as it oscillates back and forth past the equilibrium position.
4. The maximum velocity, v₀, is equal to the product of the maximum displacement, x₀, and the angular frequency, ω, and demonstrates that the maximum velocity is directly proportional to both.
5. The mathematical identity used is cos²ωt + sin²ωt = 1. This identity allows for a trigonometric expression with time to be changed into an algebraic expression with position.
6. The velocity of a horizontal spring mass model can be expressed either as a function of time, v = v₀cos(ωt), or as a function of displacement, v = ±ω√(x₀²-x²).
7. The JavaScript HTML5 applet simulates the relationship between velocity and position in a horizontal spring mass model, illustrating simple harmonic motion.
8. An example of another interactive learning tool is the "Energy Pendulum Model for Primary."
9. Embedding the model into a webpage allows users to interact with the simulation directly within a web browser, enhancing accessibility and engagement with the content.
10. The app version of the model can be accessed through the provided Google Play store link.

Essay Questions

Instructions: Answer each question in a well-structured essay format.

1. Discuss the significance of understanding the relationship between velocity and displacement in simple harmonic motion. How does this knowledge contribute to our broader understanding of oscillatory systems in physics?
2. Explain the derivation of the velocity-displacement equation in SHM, beginning with x = x₀ sin ωt, clearly outlining each step and the mathematical principles involved.
3. How can simulation tools, such as the provided JavaScript HTML5 applet, enhance students’ understanding of complex physics concepts like SHM? Discuss the benefits and potential drawbacks of using these types of tools in the learning process.
4. Considering real-world applications, analyze how the principles of simple harmonic motion are applied in various technologies and engineering designs, providing specific examples.
5. The provided text mentions various other models and simulations available within the Open Educational Resources / Open Source Physics @ Singapore. Compare and contrast the learning objectives and target audiences of at least three of them, relating your answer to how learning of physics concepts can be supported by these kinds of models.

Glossary of Key Terms

Simple Harmonic Motion (SHM): A type of periodic motion where the restoring force is directly proportional to the displacement and acts in the opposite direction. It results in oscillations around an equilibrium point.

Displacement (x): The distance of an object from its equilibrium position, with a direction from the equilibrium point.

Maximum Displacement (x₀): Also known as amplitude, this is the greatest distance an object moves from its equilibrium position in simple harmonic motion.

Velocity (v): The rate of change of displacement with respect to time; in SHM, it is not constant but varies with the position of the oscillating mass.

Maximum Velocity (v₀): The highest speed of the oscillating object in SHM, which occurs when the object is passing through the equilibrium position.

Angular Frequency (ω): A measure of how quickly an object oscillates in radians per second, indicating the rate of change of the phase of the SHM.

JavaScript HTML5 Applet: An interactive application designed using JavaScript and HTML5, allowing for dynamic simulations and visualizations in a web browser environment.

Equilibrium Position: The point in the motion of an object undergoing simple harmonic motion where the net force on the object is zero, and where the potential energy is minimized.

Oscillation: A repetitive variation, typically in time, of some measure about a central value or between two or more values. In the context of mechanics, the term typically refers to a repeated back-and-forth motion.

Trigonometric Identity: An equation that is true for all values of the variables. The trigonometric identity cos²ωt + sin²ωt = 1 allows for relationships between sine and cosine to be expressed in alternate forms.

Apps

https://play.google.com/store/apps/details?id=com.ionicframework.shm09app611123&hl=en

Video

https://notebooklm.google.com/notebook/2cb4aca0-a51f-42a6-94bf-8fc451482c6b/audio

Cast of Characters

• lookang: The user mentioned as the sole member online, likely the main administrator or lead developer of the platform. This user has a large number of articles (1169) and views (9597632) associated with their account, indicating this is a key person in the project, Loo Kang Wee.

Frequently Asked Questions

• What is the horizontal spring-mass model simulation about, and what does it demonstrate?
• The simulation, specifically the SHM09 model, explores the relationship between velocity and displacement in a horizontal spring-mass system undergoing Simple Harmonic Motion (SHM). It allows users to visualize and understand how velocity changes as the mass moves back and forth along its path, and how those changes relate to the mass's position.
• How is the velocity of the mass calculated in the simulation?
• The simulation calculates velocity (v) based on the displacement (x) from the equilibrium point. It uses the mathematical relationship derived from SHM principles: v = ±ω√(x₀² - x²), where x₀ is the maximum displacement (amplitude) and ω (omega) is the angular frequency. This formula highlights that velocity is zero at the extreme points of motion (when x=x₀) and maximum at the equilibrium point (x=0).
• What does the term "ω" (omega) represent in the simulation's velocity calculations?
• ω (omega) represents the angular frequency of the oscillation, also known as the rate at which the object rotates around the circle in radians per second. It relates to the period (T) of the oscillation by the equation ω = 2π/T and is directly proportional to how fast the mass oscillates in SHM. The higher the angular frequency, the faster the oscillations occur.
• The text mentions 'v0'. What does this represent and how is it derived?
• v0 represents the maximum velocity of the mass during its oscillation. It is derived from the equation v = x₀ω cos(ωt), where at a maximum (when cos(ωt)=1), v = x₀ω. Therefore, v0 is equal to x₀ω (amplitude multiplied by angular frequency).
• What are the key takeaways when viewing the relationship between velocity and displacement in SHM?
• The simulation demonstrates that velocity and displacement are inversely related in SHM. When the displacement is at its maximum (either side of the equilibrium), the velocity is zero as the mass momentarily stops to change direction. Conversely, when the mass passes through the equilibrium position, the displacement is zero, and the velocity is at its maximum. This cyclical relationship is characteristic of SHM.
• What tools or platforms are used for creating and running these simulations?
• The simulations are created using Easy JavaScript Simulations (EJS) and are designed to run as HTML5 applets. This means that the simulations are accessible across various platforms, including web browsers on computers, tablets, and smartphones, without the need for additional software installations.
• What are some of the other simulations that are available on the website, in addition to the horizontal spring mass model?
• The website hosts an extensive collection of interactive simulations covering a wide array of topics. Some include models of: projectile motion, wave superposition, collisions, pendulums, vector addition, electromagnetism, radioactive decay, kinematics, and many more across various levels of education, from primary to tertiary. They are not limited to physics and have expanded to other areas like chemistry, geography, mathematics and literacy.
• Who are the primary target users for these educational simulations and what is the license?
• The simulations are intended for students and educators in various subjects to aid in the visualization and understanding of different scientific and mathematical concepts. The simulations are under the Creative Commons Attribution-Share Alike 4.0 Singapore License meaning they can be shared and adapted freely as long as they are attributed to the original creators. Commercial use of the EasyJavaScriptSimulations Library requires contacting This email address is being protected from spambots. You need JavaScript enabled to view it. directly.