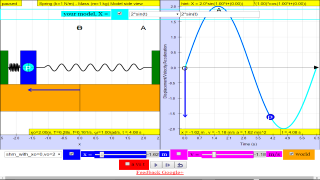
About

10.2.2 Special Case (starting from x=0) Solution to the defining equation:LO (e)*

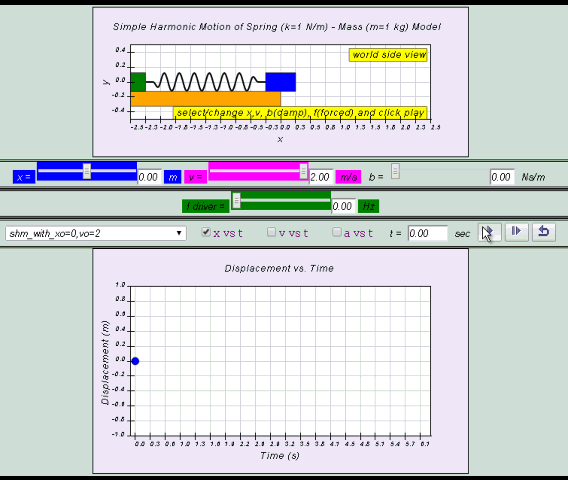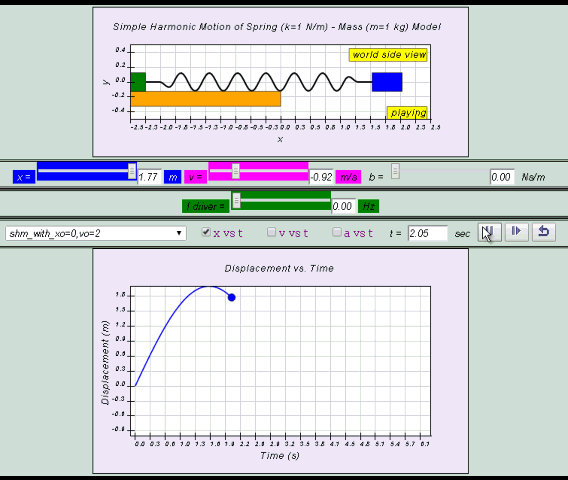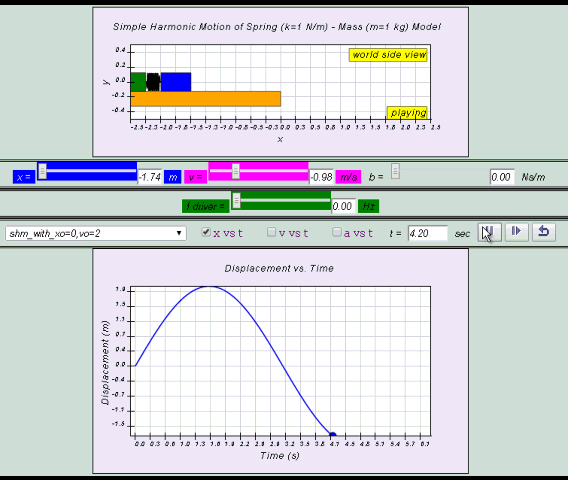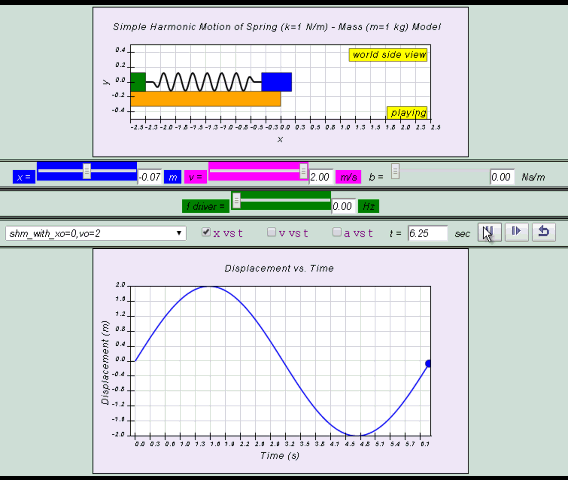
x= x₀  sin( ωt )
     

Note:

Equation for v can also be obtained by differentiating x with respect to time t.

v = x₀ ω cos (ωt ) = v₀ cos (ωt)
   

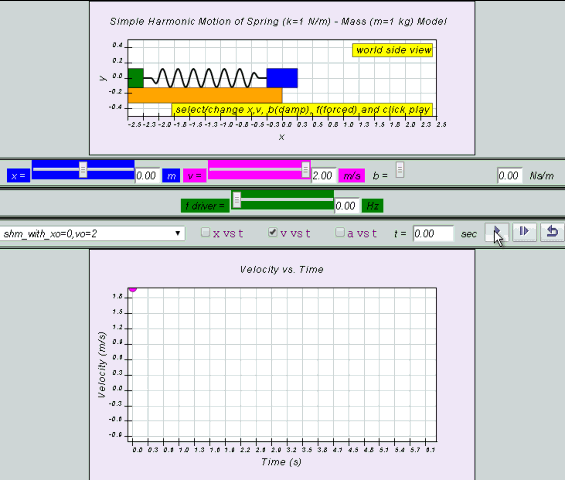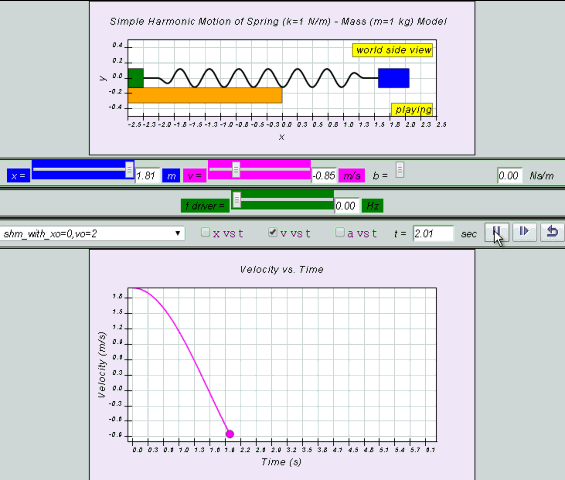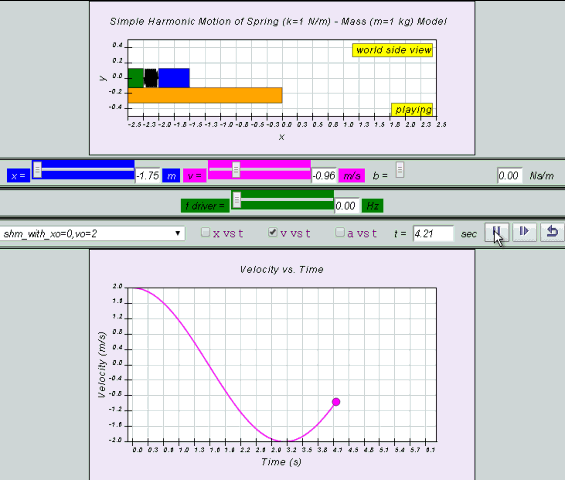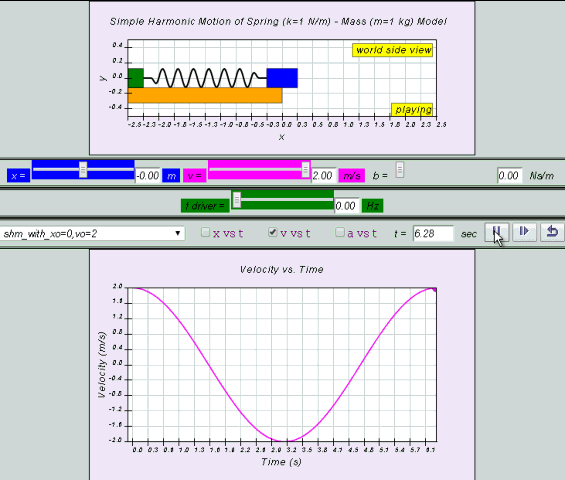
Note:

Equation for a can also be obtained by differentiating v with respect to time t.

a = - x₀ ω² sin (ωt ) = - a₀ sin (ωt)

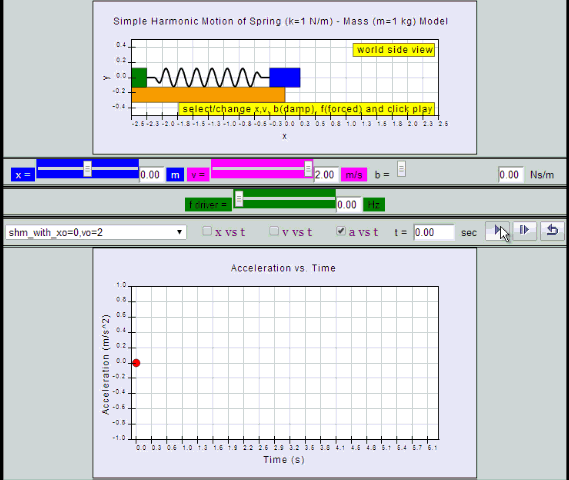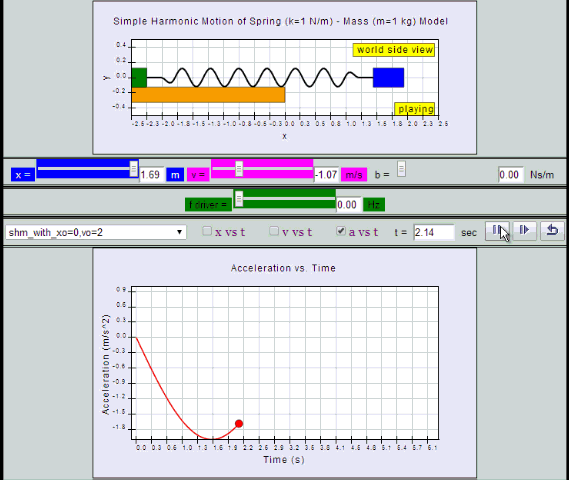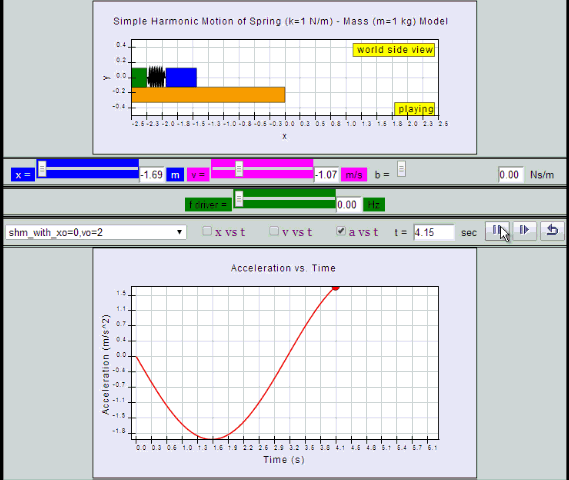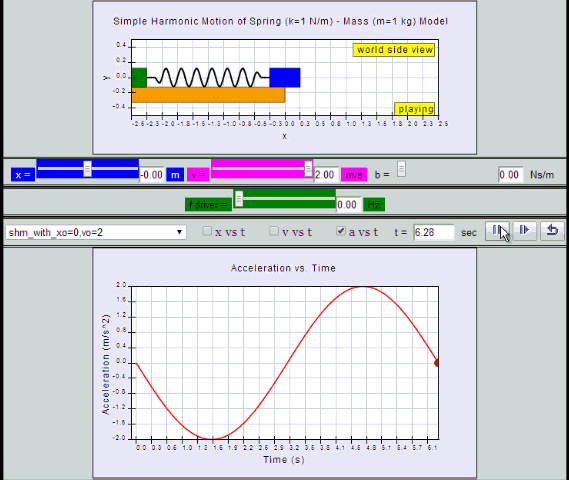
10.2.2.1 Model:

1. http://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_SHM08/SHM08_Simulation.xhtml
2. http://iwant2study.org/ospsg/index.php/interactive-resources/physics/02-newtonian-mechanics/09-oscillations/71-shm08
   

by substitution, suggest if the defining equation a =  - ω² x is true or false.

10.2.2.2 Suggest there Special Case (starting from x=x₀ ) Solution to the defining equation:LO (e) if given

x= x₀  cos( ωt )
v = -x₀ ω sin (ωt ) = -v₀ sin (ωt)
a = -x₀ ω² cos (ωt ) = - a₀ cos (ωt)

by substitution, suggest if the defining equation a =  - ω² x is true or false.

10.2.2.3 Summary:

Quantity	extreme left	centre equilibrium	extreme right
x	– x0	0	x0
v	0	+ x0ω when v >0 or – x0ω when v <0 which are maximum values	0
a	+x0ω2	0	–x0ω2

 

Translations

Code	Language		Translator	Run

Credits

This email address is being protected from spambots. You need JavaScript enabled to view it.

http://iwant2study.org/lookangejss/02_newtonianmechanics_8oscillations/ejss_model_SHM08/SHM08_Simulation.xhtml

Briefing Document: Simple Harmonic Motion (SHM) and Associated Simulations

1. Introduction

This document provides a summary of the key concepts and ideas presented in the provided source, "10.2.2 Defining Equation of Simple Harmonic Motion and Horizontal Spring Mass Model A vs T," from Open Educational Resources / Open Source Physics @ Singapore. The source focuses on defining and explaining Simple Harmonic Motion (SHM) through equations and interactive simulations. The material is intended for a Junior College level audience and is accessible on various platforms (Windows, MacOS, Linux, Chromebooks, Android/iOS devices)

2. Core Concepts of Simple Harmonic Motion

• Defining Equation: The fundamental concept is the defining equation of SHM, which relates acceleration (a) to displacement (x) with the angular frequency (ω):
• Equation: a = - ω² x
• This equation indicates that the acceleration of an object in SHM is directly proportional to its displacement and acts in the opposite direction.
• Displacement, Velocity and Acceleration equations:
• The document presents two special case scenarios for deriving the equations for displacement (x), velocity (v), and acceleration (a). These are based on different starting conditions:
• Case 1: Starting from x=0Displacement x = x0 sin(ωt)
• Velocity v = x0 ω cos(ωt) = v0 cos(ωt)
• Acceleration a = - x0 ω² sin(ωt) = - a0 sin(ωt)
• Case 2: Starting from x=x0Displacement x = x0 cos(ωt)
• Velocity v = -x0 ω sin(ωt) = -v0 sin(ωt)
• Acceleration a = -x0 ω² cos(ωt) = - a0 cos(ωt)
• Note: x0 represents the amplitude, v0 the maximum velocity, and a0 the maximum acceleration. The equations are obtained by differentiating x with respect to time for velocity, and differentiating v with respect to time for acceleration.
• Verification by Substitution: The document emphasizes verifying the core equation, a = - ω² x, by substituting the derived expressions for x and a for both special cases into this equation. This process confirms that the relationships are consistent with the defining equation of SHM.
• Summary of Position, Velocity and Acceleration at Extreme and Equilibrium Positions
• The document summarizes the position, velocity, and acceleration values at three key points during the oscillation: extreme left, centre equilibrium, and extreme right.
• Extreme Left: Displacement is -x0, velocity is 0, acceleration is +x0ω².
• Centre Equilibrium: Displacement is 0, velocity is either + x0ω or – x0ω (depending on direction), acceleration is 0.
• Extreme Right: Displacement is +x0, velocity is 0, acceleration is -x0ω².
• These summaries help students understand the relationship between position, velocity and acceleration in simple harmonic motion.

3. Interactive Simulations

• Embeddable Models: The source includes links to interactive simulations built using Easy JavaScript Simulation (EJS). These models are designed to be embedded in web pages using <iframe> tags, making them easily accessible for students.
• Simulation 1: http://dl.dropboxusercontent.com/u/44365627/lookangEJSworkspace/export/ejss_model_SHM08/SHM08_Simulation.xhtml
• Simulation 2: http://iwant2study.org/ospsg/index.php/interactive-resources/physics/02-newtonian-mechanics/09-oscillations/71-shm08
• Purpose of Simulations: The simulations likely allow users to visualize the motion of a mass-spring system, observe the changes in position, velocity, and acceleration over time, and relate these to the derived mathematical equations.
• Accessibility: The simulations are designed to be used on various devices, including laptops, desktops, Chromebooks, smartphones, and tablets, ensuring broad accessibility for learners.

4. Educational Context and Use

• Junior College Level: The content is specifically targeted at students in junior college, indicating that it is designed to support higher-level physics curricula.
• Open Educational Resource: As part of the Open Educational Resources / Open Source Physics @ Singapore initiative, the materials are freely available for educational use under a Creative Commons license.
• Technology Integration: The content highlights the use of interactive JavaScript simulations for learning, promoting a modern, technology-driven approach to physics education.
• Integration with SLS: There is mention of the simulations being used with Student Learning Space (SLS) with a focus on interactive learning.

5. Additional Notes and Resources

• Related Simulations: The page contains links to a wide array of other interactive simulations covering topics such as:
• Energy Pendulums
• Newton's Cradle
• Projectile Motion
• Wave Phenomena
• Electromagnetism and more.
• EJS (Easy JavaScript Simulation) Library: The page highlights the use of EJS as the tool for creation of these simulations.
• Teacher Resources: Mention is made about customizable teacher versions and the use of simulations in Teacher Learning Communities.
• Licensing: The materials are licensed under Creative Commons Attribution-Share Alike 4.0 Singapore License with separate commercial use terms for the EasyJavaScriptSimulations Library.

6. Key Takeaways

• The document and linked simulations provide a comprehensive approach to understanding Simple Harmonic Motion, combining mathematical rigor with interactive visualization.
• The use of JavaScript simulations makes complex concepts more accessible and engaging for students.
• The materials are openly available, promoting collaborative learning and resource sharing.
• The wide variety of additional simulations highlight a diverse range of topics suitable for secondary and college level students.

7. Conclusion

This briefing document has summarized the core information from the provided source, which focuses on the defining equations of SHM and how they can be visualized through interactive JavaScript simulations. The combination of mathematical explanations, practical applications, and diverse examples makes the material a valuable resource for physics educators and students.

Simple Harmonic Motion Study Guide

Quiz

Instructions: Answer the following questions in 2-3 sentences each.

1. What is the defining characteristic of Simple Harmonic Motion (SHM)?
2. In the context of a horizontal spring-mass system, what does x represent in the equations of SHM?
3. If an object undergoing SHM starts at x=0, what is the mathematical expression for its displacement (x) as a function of time (t)?
4. How is the velocity of an object undergoing SHM derived from its displacement equation?
5. What is the mathematical relationship between acceleration (a) and displacement (x) in SHM?
6. What is the significance of ω (omega) in the equations of motion for SHM?
7. When an object in SHM is at its extreme right position, what is its velocity?
8. When an object in SHM is at the center equilibrium point, what is its acceleration?
9. What is the equation for displacement (x) as a function of time when the motion starts at x=x₀?
10. How does the maximum value of velocity relate to maximum displacement (x₀) and angular frequency ω?

Quiz Answer Key

1. Simple Harmonic Motion (SHM) is defined by a motion where the acceleration of an object is directly proportional to its displacement from the equilibrium position and is always directed towards that position. This restorative force results in a consistent back and forth motion around the equilibrium point.
2. In the context of a horizontal spring-mass system, x represents the displacement of the mass from its equilibrium position. It indicates how far the mass has moved to the left or right of its resting or centered location.
3. If the object starts at x=0, the displacement (x) is given by the equation x = x₀sin(ωt), where x₀ is the maximum displacement, ω is the angular frequency, and t is time. This function describes a sinusoidal motion starting at the equilibrium position.
4. The velocity of an object in SHM is obtained by differentiating the displacement equation with respect to time (t). This derivative yields a new function that describes how the position is changing at every point in the motion.
5. In SHM, the acceleration (a) is directly proportional and opposite to the displacement (x) and related through the expression a = -ω²x. This implies that when displacement increases positively, acceleration increases in a negative direction.
6. ω (omega) represents the angular frequency of the oscillation, determining how rapidly the object oscillates. It is related to the period (T) and frequency (f) of the motion, which are key to understanding how fast cycles occur.
7. When an object in SHM is at its extreme right position, its velocity is instantaneously zero. At these turning points, the object momentarily stops before reversing its direction.
8. When an object in SHM is at the center equilibrium point, its acceleration is zero. At the center point the net force is zero, resulting in zero acceleration.
9. When the motion starts at x=x₀, the displacement is expressed as x = x₀cos(ωt). This function describes a sinusoidal motion that starts at its maximum displacement point.
10. The maximum value of velocity (v₀) is related to the maximum displacement (x₀) and angular frequency (ω) by the equation v₀= x₀ω. This expression shows that velocity and displacement are directly linked to the speed of the motion.

Essay Questions

Instructions: Answer each of the following questions in a well-organized essay format with supporting information from the provided materials.

1. Explain how the defining equation of Simple Harmonic Motion (a = -ω²x) can be derived and interpreted from the displacement, velocity, and acceleration equations for both initial conditions (x=0 and x=x₀).
2. Compare and contrast the equations for displacement, velocity, and acceleration when an object undergoing SHM starts at the equilibrium position (x=0) and when it starts at its maximum displacement (x=x₀). Discuss how these equations change based on initial conditions.
3. Analyze the relationships between displacement, velocity, and acceleration over a complete cycle of Simple Harmonic Motion. Include specific descriptions of what is happening at the extreme left, center equilibrium, and extreme right points of the motion.
4. Using the provided equations, describe how changes in the angular frequency (ω) would affect the period, frequency, velocity, and acceleration of an object in Simple Harmonic Motion.
5. Discuss how the provided SHM equations can be used to model and understand the motion of a mass on a horizontal spring and discuss the limitations of this model.

Glossary of Key Terms

Simple Harmonic Motion (SHM): A type of periodic motion where the restoring force is directly proportional to the displacement and acts in the opposite direction to the displacement.

Displacement (x): The distance of an object from its equilibrium position at any given time. This is a measure of position relative to the resting state of the oscillating object.

Velocity (v): The rate of change of displacement with respect to time. It indicates how fast an object is moving and in what direction as it oscillates.

Acceleration (a): The rate of change of velocity with respect to time. In SHM, it is proportional to and opposite of displacement.

Angular Frequency (ω): A measure of how fast an object is oscillating, related to the frequency (f) and period (T) by the equations ω=2πf and ω=2π/T.

Equilibrium Position: The central point where the net force on the oscillating object is zero. It is where the mass is at rest in the absence of any oscillation.

Maximum Displacement (x₀): The greatest displacement of the object from its equilibrium position. This corresponds to the amplitude of the oscillation.

Period (T): The time it takes for one complete cycle of motion in Simple Harmonic Motion. This would be for example, the time for a mass to move left and right and return to its starting position.

Frequency (f): The number of complete cycles of motion completed per unit of time. The frequency and period are inversely proportional to one another.

Video

https://notebooklm.google.com/notebook/9e94c347-6341-4745-bb77-02021eb236f1/audio

Frequently Asked Questions About Simple Harmonic Motion (SHM)

1. What is the defining equation of Simple Harmonic Motion (SHM), and how is it represented mathematically? The defining equation of SHM is a = -ω²x, where 'a' represents acceleration, 'ω' (omega) represents angular frequency, and 'x' represents displacement from the equilibrium position. This equation demonstrates that the acceleration of an object in SHM is directly proportional to its displacement but acts in the opposite direction (hence the negative sign). The constant of proportionality is the square of the angular frequency. This relationship is fundamental in understanding SHM.
2. How does the displacement of an object undergoing SHM change over time, specifically when starting from the equilibrium position (x=0)? When an object starts from the equilibrium position (x=0), its displacement can be described by the equation x = x₀ sin(ωt). Here, x₀ represents the amplitude (maximum displacement), ω is the angular frequency, and t is time. This equation shows that the displacement varies sinusoidally with time, starting at zero, reaching a maximum at x₀ and then returning to the equilibrium position in an oscillatory fashion.
3. How do the velocity and acceleration equations relate to displacement in SHM when starting from the equilibrium position (x=0)? When starting from x=0, the velocity, v, is represented as v = x₀ω cos(ωt) = v₀ cos(ωt), where v₀ is the maximum velocity. The acceleration, a, is given by a = -x₀ω² sin(ωt) = -a₀ sin(ωt), where a₀ is the maximum acceleration. These equations are derived by successively differentiating the displacement equation with respect to time. Notice that the acceleration is always out of phase with the velocity by 90 degrees and exactly 180 degrees out of phase with the displacement when starting from the equilibrium position.
4. If an object starts its SHM from its extreme position (x=x₀), how is its displacement, velocity and acceleration over time different compared to when it starts at equilibrium? When SHM starts at an extreme position (x = x₀), the displacement is represented by x = x₀ cos(ωt). The velocity is given by v = -x₀ω sin(ωt) = -v₀ sin(ωt), and the acceleration by a = -x₀ω² cos(ωt) = -a₀ cos(ωt). Starting at an extreme position results in a cosine function for displacement and acceleration, whereas it results in a sine function for velocity, and is exactly 180 degrees out of phase with displacement. The main difference is that the position begins at maximum amplitude rather than at zero.
5. Can you summarize the relationships between displacement, velocity and acceleration in SHM at the extreme left, equilibrium, and extreme right positions?

• Extreme Left: At the extreme left, displacement (x) is -x₀, velocity (v) is 0, and acceleration (a) is +x₀ω².
• Centre/Equilibrium: At the equilibrium position, x is 0, velocity v is at its maximum which is +x₀ω when moving to the right, or -x₀ω when moving to the left, and acceleration a is 0.
• Extreme Right: At the extreme right, displacement (x) is +x₀, velocity (v) is 0, and acceleration (a) is -x₀ω².

1. How can the provided interactive simulations help in understanding Simple Harmonic Motion (SHM)? The interactive simulations, specifically the linked models, like SHM08_Simulation.xhtml, can visually demonstrate the relationships between displacement, velocity, and acceleration in real-time. These simulations allow users to manipulate parameters and observe how these changes affect the motion. This hands-on experience is very valuable to see how the object moves and for visualizing the phase relationships between position, velocity and acceleration.
2. How are the equations for SHM derived and what do they tell us? The equations for SHM are derived using calculus by analyzing the relationship between displacement, velocity and acceleration with respect to time. The velocity equation can be obtained by differentiating the displacement equation with respect to time. The acceleration equation can be obtained by differentiating the velocity equation with respect to time. The equations show that position, velocity and acceleration are sinusoidal functions that are out of phase with each other and that the acceleration is proportional and opposite in direction to the displacement of the object.
3. What is the significance of ω (omega) in the SHM equations, and how does it relate to the period and frequency of oscillations? ω, the angular frequency, is a crucial parameter. It is related to the frequency (f) of oscillations through ω = 2πf. The period (T), which is the time taken for one full oscillation, is linked by T = 1/f or T = 2π/ω. ω determines how rapidly the object oscillates back and forth in SHM, essentially defining the time scale of the motion.