About

For Teachers

- 311_27_srimagima_ptvid_50cm_3lookang.mp4

Credits

Author: video: srimagima, model: lookang
Contact: This email address is being protected from spambots. You need JavaScript enabled to view it.

Document Brief: Modeling Pendulum Dynamics Using Tracker

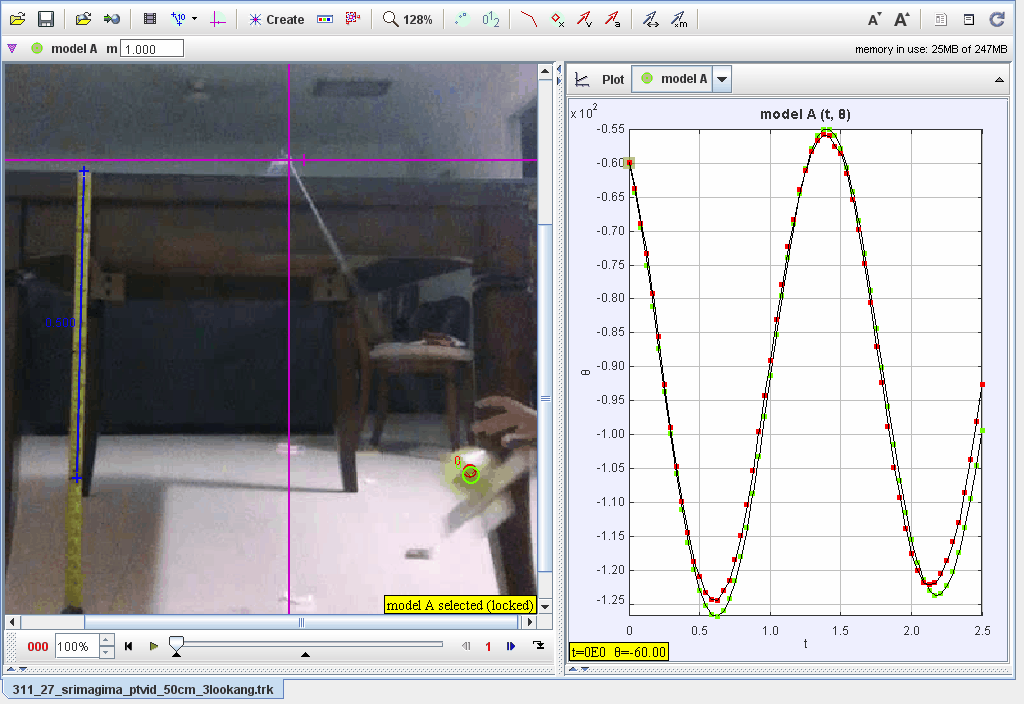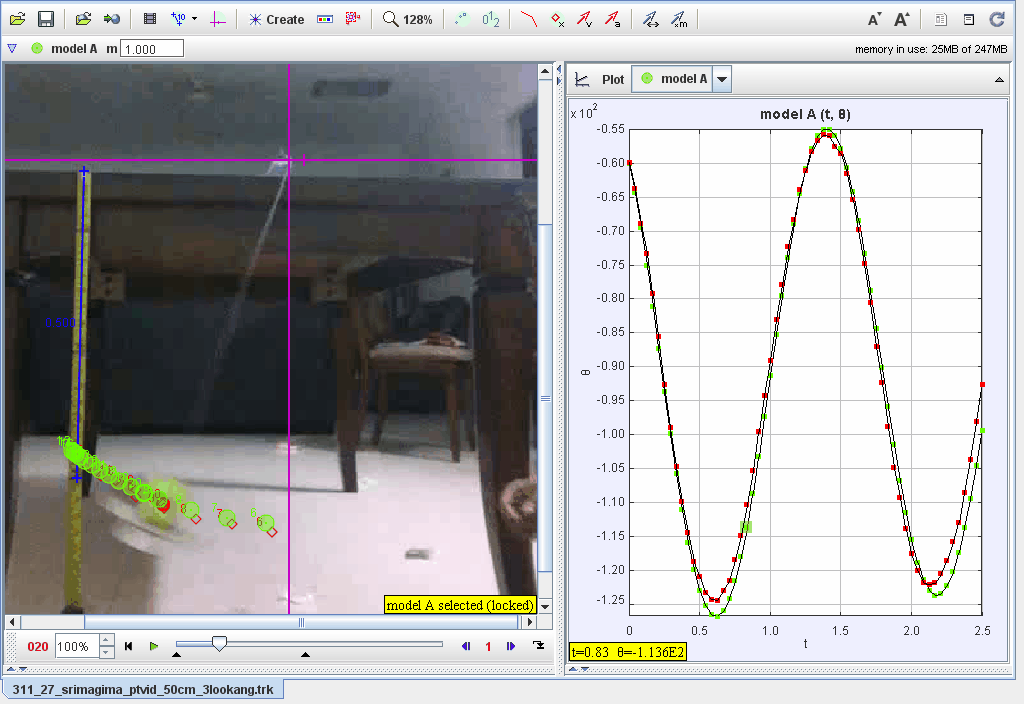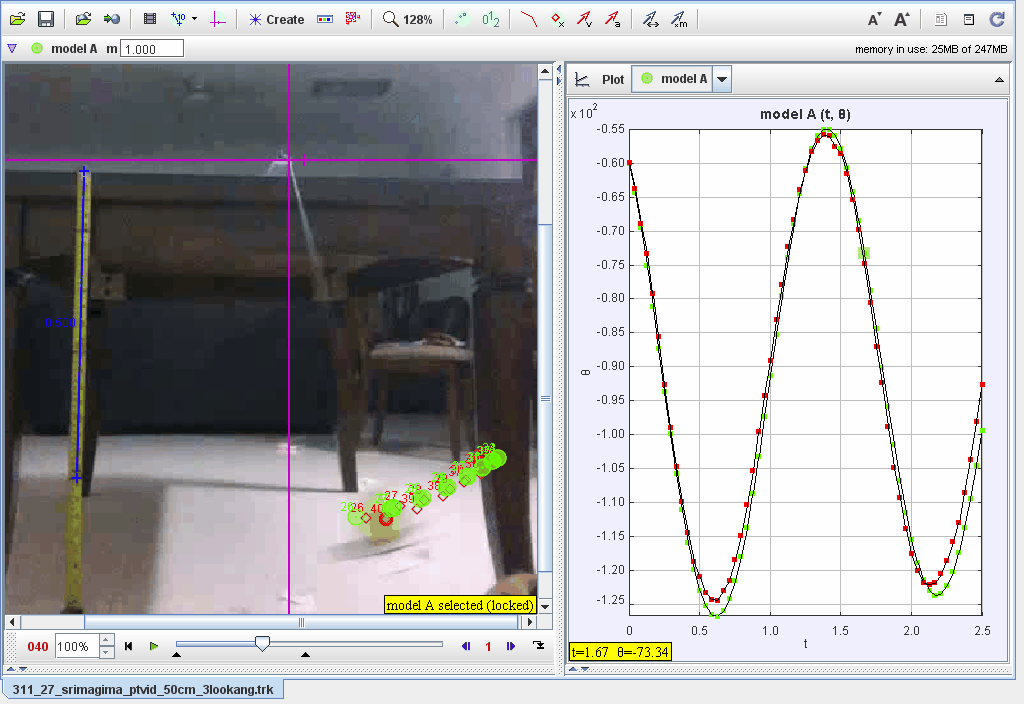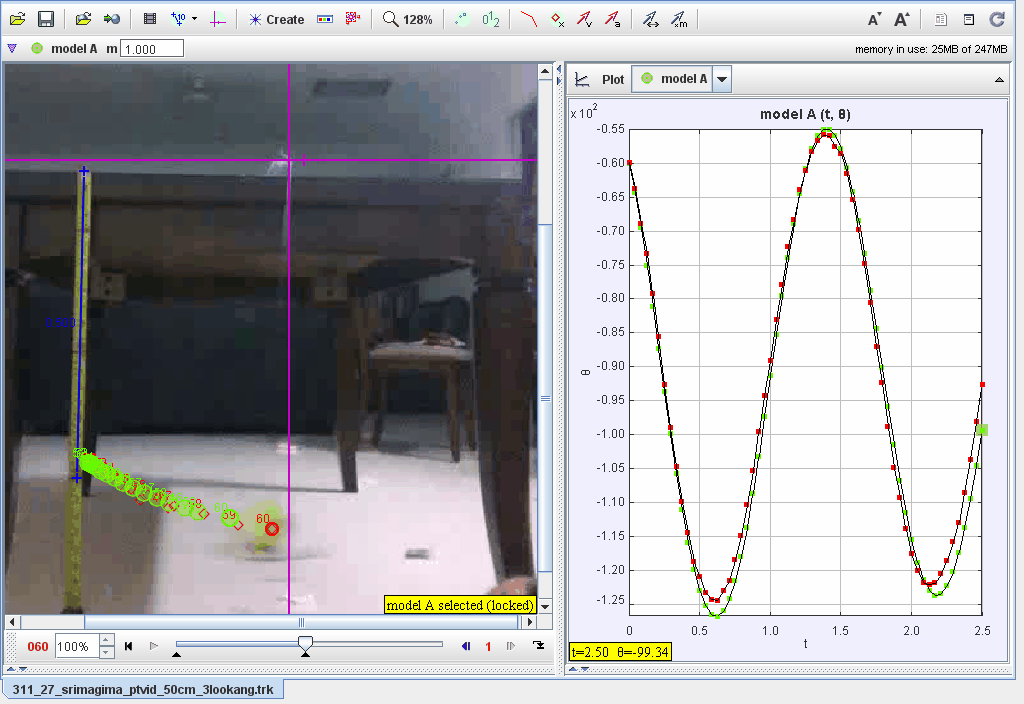
This document provides an analysis of a pendulum motion using Tracker’s dynamic particle modeling tool in polar coordinates. The motion of the pendulum is analyzed through angular displacement ($\theta$), angular velocity ($\omega$), and angular acceleration ($\alpha$), incorporating damping and restoring forces.

Purpose:

To study the oscillatory motion of a pendulum by modeling forces acting on it, analyzing its behavior over time, and validating experimental data against theoretical predictions.

Key Features:

• Dynamic particle modeling in polar coordinates.
• Force functions:
  • Restoring force: Fθ=−m⋅g⋅cos⁡(θ)−k⋅ω⋅r,
  • Radial force: Fr=−m⋅r⋅ω^2
• Graphical analysis of angular displacement (θ), velocity (ω, and acceleration (α) vs. time ($t$).

Study Guide: Modeling Pendulum Motion with Damping

Learning Objectives:

1. Understand the forces acting on a pendulum, including damping and restoring forces.
2. Analyze oscillatory motion using angular displacement, velocity, and acceleration.
3. Validate the damping coefficient ($k$) and its effect on motion.

Step-by-Step Guide:

1. Setup and Calibration:

   • Import the video of the pendulum into Tracker.
   • Calibrate the coordinate system using a visible reference (e.g., a ruler) for accurate scaling.

2. Tracking Motion:

   • Track the pendulum’s position frame by frame.
   • Record angular displacement ($\theta$) data in polar coordinates.

3. Modeling Forces:

   • Open Tracker’s Model Builder and set parameters:
     • m=1.0 kg (mass),
     • g=10 m/s^2 (gravitational acceleration),
     • k=0.11 (damping coefficient),
     • r=0.59 m (pendulum length).
   • Define initial values:
     • θ0=−60∘,
     • $/\text{s}$.
   • Apply force functions:
     • Fr=−m⋅r⋅ω^2,
     • Fθ=−m⋅g⋅cos⁡(θ)−k⋅ω⋅r

4. Graphical Analysis:

   • Plot θ, ω, and $\alpha$ vs. $t$:
     • Observe sinusoidal oscillations with gradual amplitude decay due to damping.
     • Analyze how the damping coefficient affects the amplitude over time.
   • Verify the period and compare theoretical and experimental data.

5. Applications:

   • Study the effects of damping in pendulum-based systems.
   • Analyze pendulum dynamics for practical applications like clocks or sensors.

Tips for Success:

• Ensure precise tracking of the pendulum bob for accurate motion data.
• Cross-check theoretical parameters against experimental data for validation.

FAQ: Pendulum Motion with Damping

1. What forces act on the pendulum in this model?

The forces include:

• Restoring force: Fθ=−m⋅g⋅cos⁡(θ)−k⋅ω⋅r,
• Radial force: Fr=−m⋅r⋅ω^2.

2. What is the role of the damping coefficient ($k$)?

The damping coefficient ($k$) represents the resistance (e.g., air friction), which reduces the amplitude of oscillation over time.

3. Why does the amplitude decay over time?

The amplitude decays due to damping, which dissipates energy from the system as heat or sound.

4. How is the period of motion affected by damping?

For light damping, the period remains nearly constant. Significant damping may slightly increase the period.

5. What is the significance of angular displacement (θ)?

Angular displacement describes the pendulum’s position relative to its equilibrium. Its sinusoidal behavior indicates periodic motion.

6. How does this model apply to real-world systems?

This model is used to:

• Design pendulum-based systems like clocks and sensors,
• Understand damping effects in engineering systems,
• Explore oscillatory behavior in physical systems.

7. Can this model handle heavy damping?

No, the current model assumes light damping. For heavy damping, additional terms and equations must be used.