About

7.4.3.2 Example

An Earth satellite of mass 200 kg is in stable circular motion orbit, calculate the launch speed for a distance of 2 R_Earth from centre of Earth.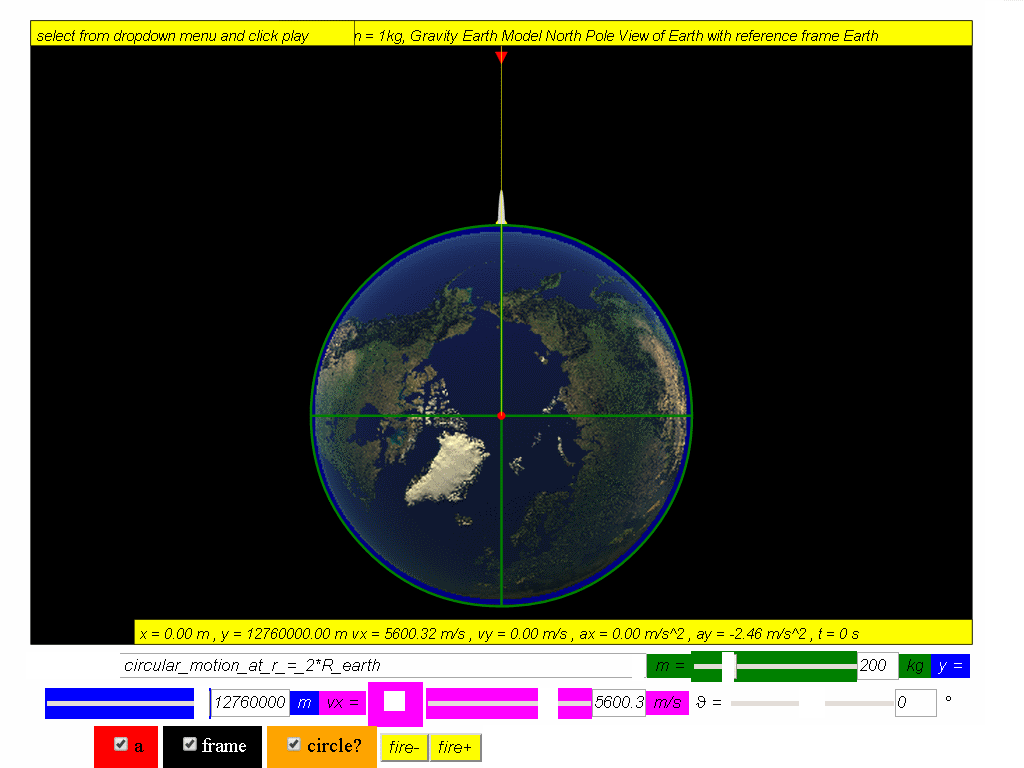


Answer: 5600 m/s

Calculate the potential energy, kinetic and total energy in this orbit.

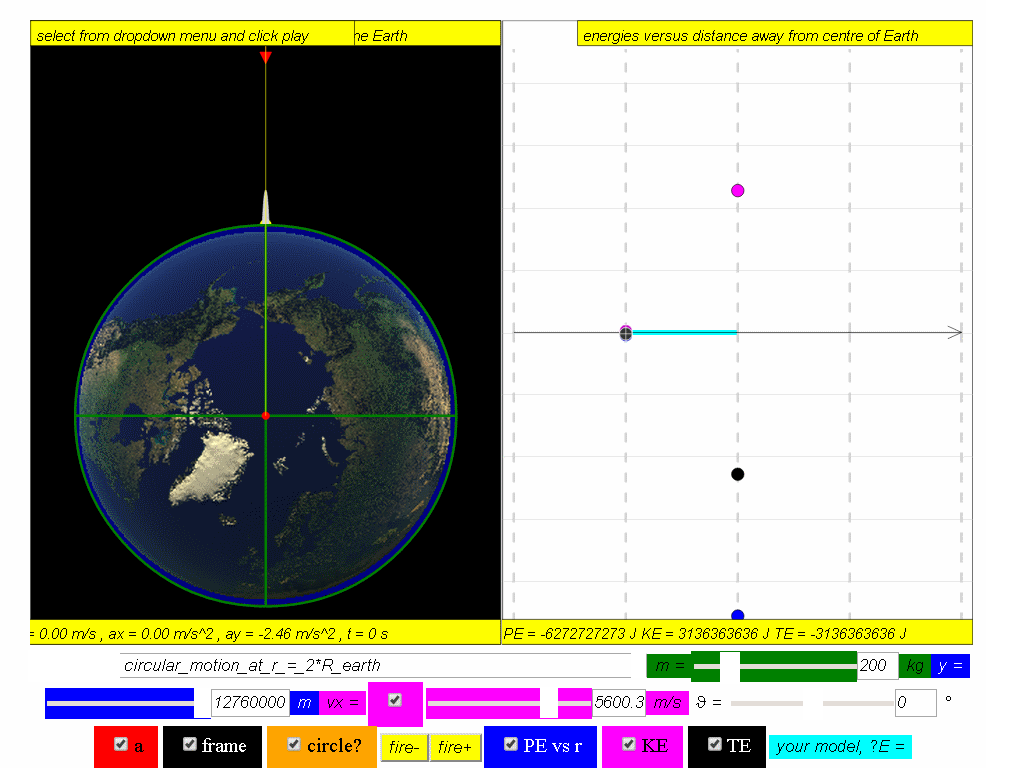
Answer: PE = -6.27x10⁷ J, KE = 3.14x10⁷ J, TE = -3.13x10⁷ J.

Calculate the value of the gravitational potential at this point.

Answer: ϕ = 3.14x10 ⁵ J/kg

Calculate the value of the gravitational acceleration at this point and state its direction.

Answer: a = 2.46 m/s² towards centre of Earth

Calculate the value of the gravitational force on the satellite at this point and state its direction.

Answer: F = 492 N towards centre of Earth

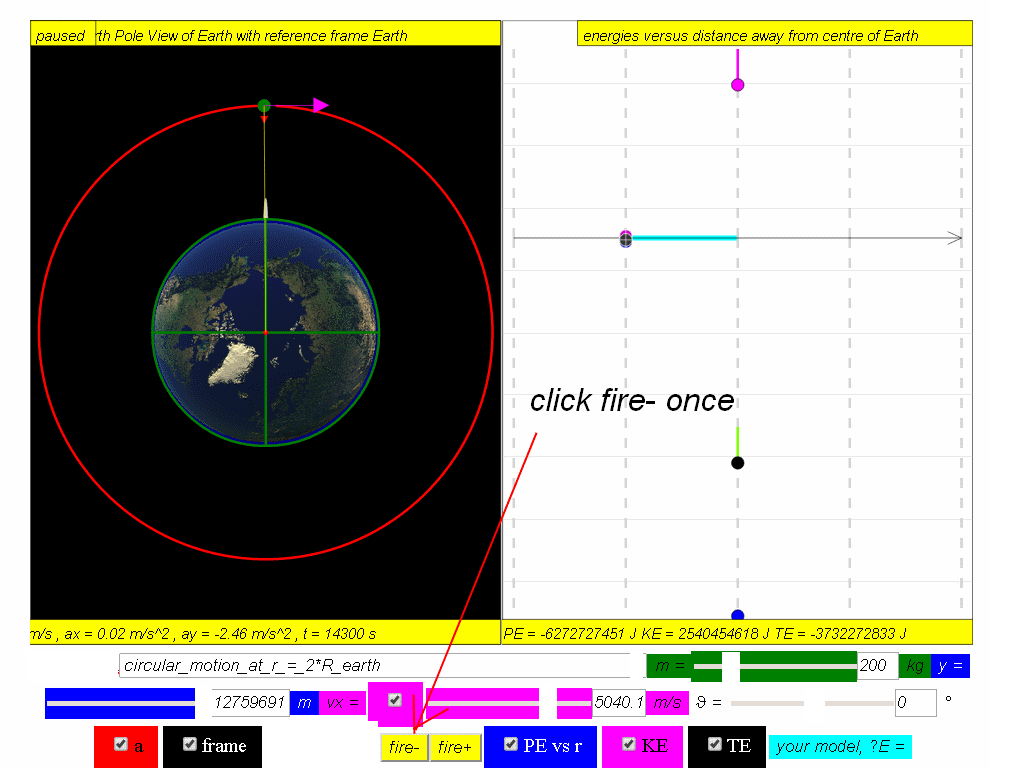
At this point of the motion, the satellite fires (click the fire- button) backward thrusters to reduce its speed.


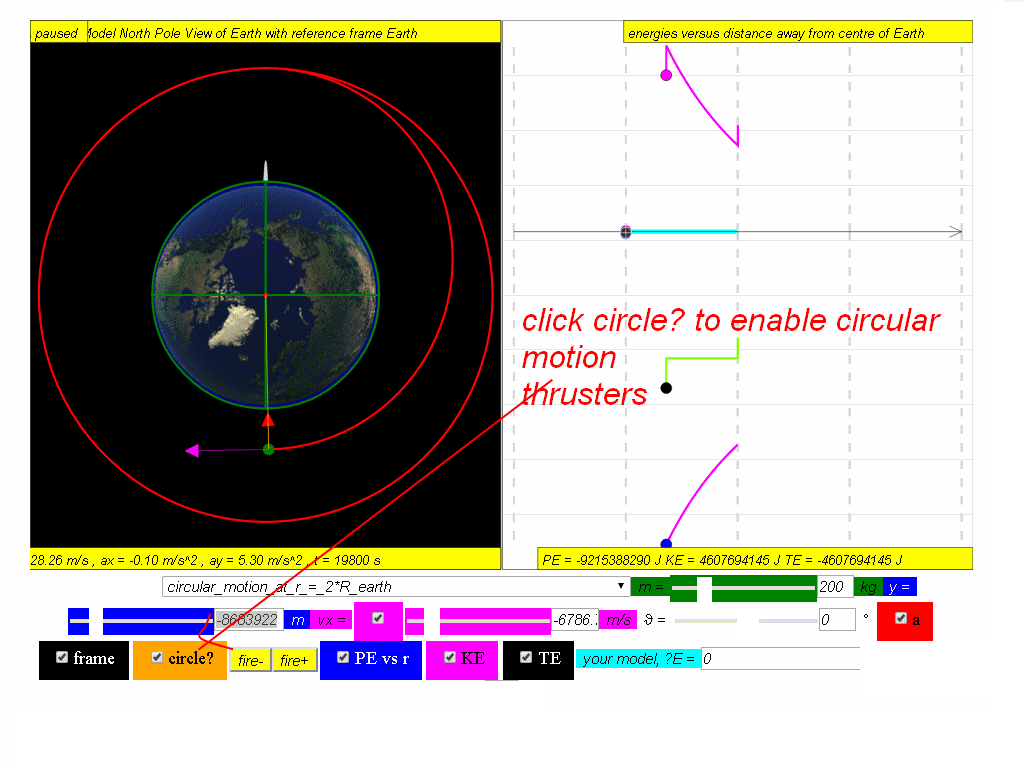
The orbits path decays to a point where it shoots some circular motion thrusters and goes on a lower circular motion.


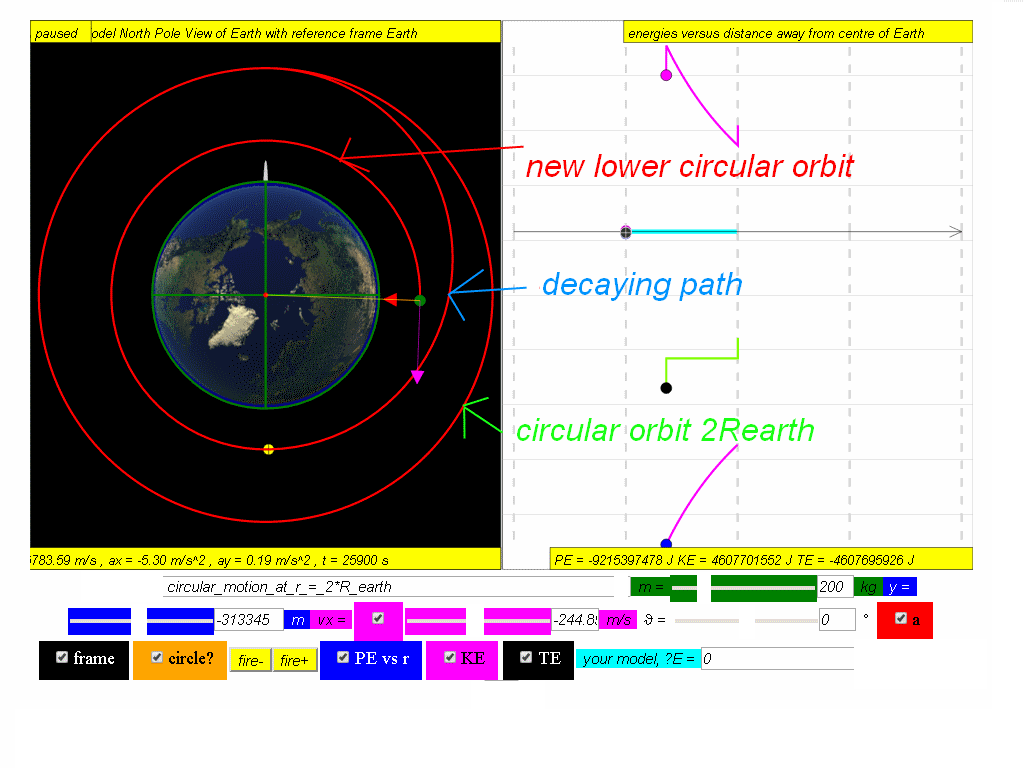
Calculate the new potential energy, kinetic and total energy in this lowered orbit, given the new radius of orbit is approximately 8.68x10⁶ m

Answer: PE = -9.22x10⁷ J, KE = 4.61x10⁷ J, TE = -4.61x10⁷ J.


Hence or otherwise, calculate the changes in the potential, kinetic and total energies of the satellite as a result of this transition. (Mass of Earth = 6.0 x 10²⁴ kg)

Answer: ΔPE = -2.95x10⁷ J, ΔKE = 1.47x10⁷ J, ΔTE = -1.48x10⁷ J.

With the diagrams below or otherwise, describe

(a) the significance of the different parts of (1,2 & 3) the graph of KE for the complete motion above.

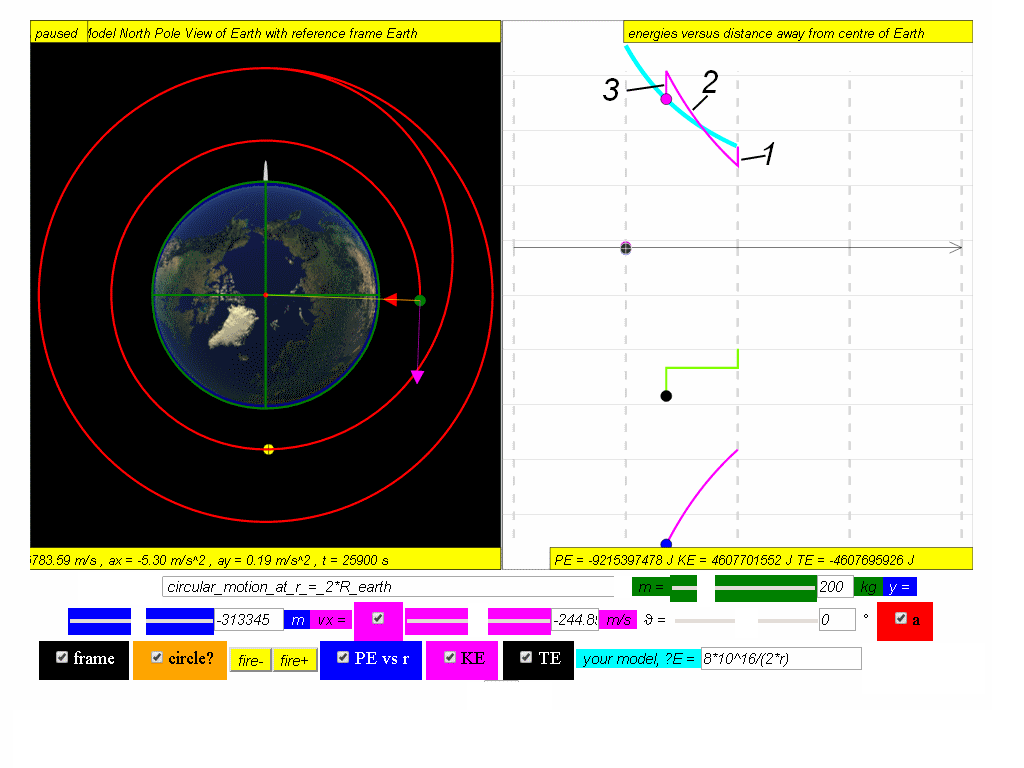
Suggested answers
1. fire reverse thrusters to begin decay path that results in decrease of KE
2. increase in speed as PE decrease and KE increase
3. fire circular motion thrusters to begin lower circular motion orbit to meet the model $KE=\genfrac{}{}{0.1ex}{}{GmM}{2r}=\genfrac{}{}{0.1ex}{}{6.67x10^{-11}\left(200\right)\left(6.0x10^{24}\right)}{2r}=\genfrac{}{}{0.1ex}{}{8x10^{16}}{2*r}$

(b) the significance of the different parts of the graph of PE for the complete motion above.

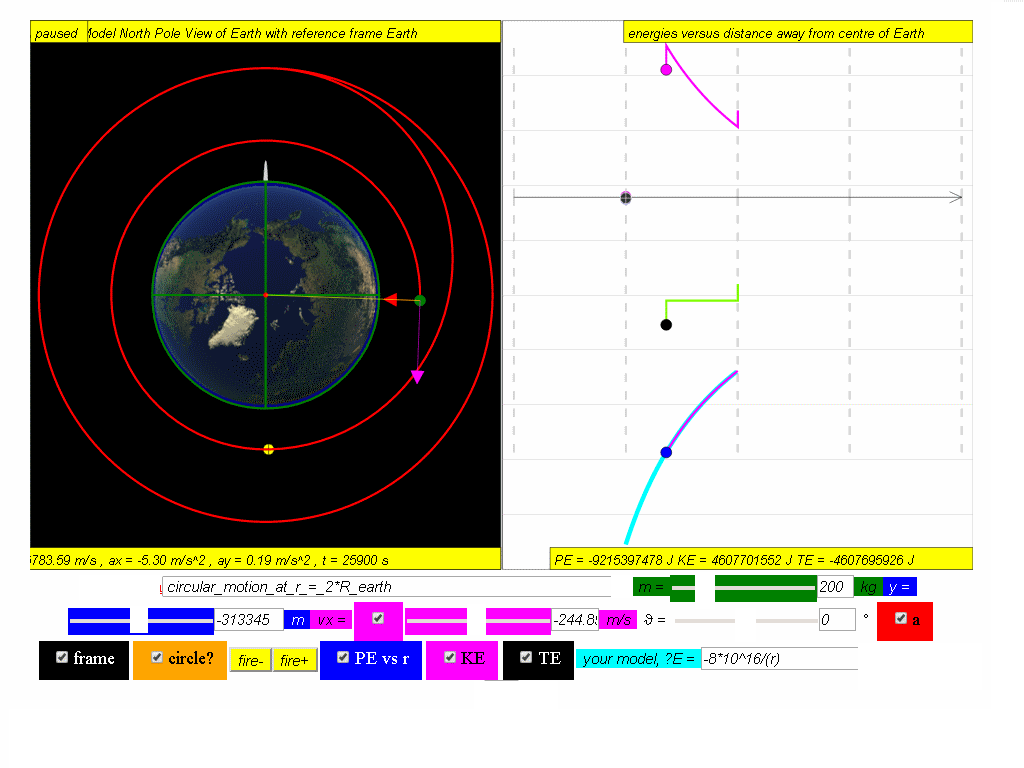
Suggested answers
the PE graph move according to the equation $U=-m\genfrac{}{}{0.1ex}{}{GM}{r}$ = mϕ from r = 2R_earth to the lower orbit from right to left


(c) the significance of the different parts of the graph of TE for the complete motion above.


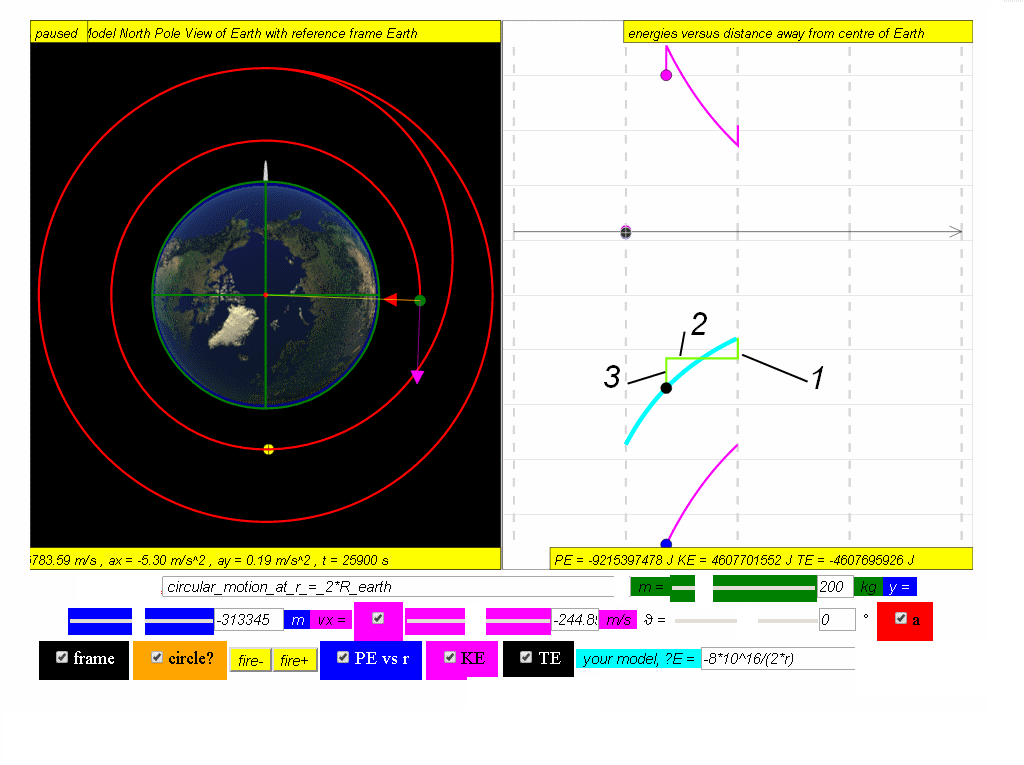
Suggested answers
1. fire reverse thrusters to begin decay path result in decrease of KE thus a corresponding decrease in TE
2. TE is constant
3. fire circular motion thrusters to begin lower circular motion orbit, results in decrease of KE and a corresponding decrease in TE to meet the model $TE=-\genfrac{}{}{0.1ex}{}{GmM}{2r}=-\genfrac{}{}{0.1ex}{}{6.67x10^{-11}\left(200\right)\left(6.0x10^{24}\right)}{2r}=-\genfrac{}{}{0.1ex}{}{8x10^{16}}{2*r}$

7.4.3.2.1 Model

1. Run Sim
2. http://iwant2study.org/ospsg/61

 

Translations

Code	Language		Translator	Run

Credits

Todd Timberlake, this remixed version is by lookang (This email address is being protected from spambots. You need JavaScript enabled to view it.); lookang; fu-kwun hwang

http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejss_model_gravity08_2/gravity08_2_Simulation.xhtml

🚀

Briefing Document: Newton's Mountain and Escape Velocity Simulation

1. Overview

This document reviews the "Newton's Mountain and Escape Velocity JavaScript HTML5 Applet Simulation Model" found on the Open Educational Resources / Open Source Physics @ Singapore website. This simulation is designed as an educational tool to illustrate key concepts in Newtonian mechanics and gravity, particularly focusing on orbital motion, energy transformations, and escape velocity. The simulation is accessible across various platforms, including web browsers, Android, and iOS devices, making it a versatile learning resource. The model, named gravity08_2, allows users to visualize and manipulate the motion of a satellite around Earth.

2. Key Themes and Concepts

• Orbital Mechanics: The core of the simulation is exploring the principles behind stable circular motion orbits and how a satellite transitions between different orbits. It demonstrates how initial velocity and thruster firings can lead to orbital decay or changes in orbital path.
• Energy Transformations: The simulation emphasizes the interplay between kinetic energy (KE), potential energy (PE), and total energy (TE) of the satellite. It shows how these energies change as the satellite's orbit changes. Specifically, the simulation allows users to observe:
• Decreasing KE: "fire reverse thrusters to begin decay path that results in decrease of KE"
• Increased KE with Decreased PE: "increase in speed as PE decrease and KE increase"
• Lowered Orbit Resulting in Lowered TE: "fire circular motion thrusters to begin lower circular motion orbit, results in decrease of KE and a corresponding decrease in TE"
• Gravitational Force and Acceleration: The simulation presents calculations and visualization of gravitational force and acceleration at different points in the satellite’s orbit. Users can see how these values are directed towards the center of the Earth and can observe how they change with orbital radius.
• Calculations and Numerical Examples: The resource provides several calculations related to a satellite in orbit. It provides the following values:
• Launch Speed: Calculation of launch speed (5600 m/s) for a distance of 2 REarth
• Energy Values: Detailed calculations of Potential Energy (PE), Kinetic Energy (KE) and Total Energy (TE) at different orbits with associated numerical values at 2 Earth Radii from center of Earth as PE = -6.27x107 J, KE = 3.14x107 J, TE = -3.13x107 J and at 8.68x106 m from center of Earth, PE = -9.22x107 J, KE = 4.61x107 J, TE = -4.61x107 J.
• Gravitational Potential: Calculation of the value of gravitational potential (ϕ = 3.14x10 5 J/kg).
• Gravitational Acceleration: Calculation of gravitational acceleration (a = 2.46 m/s2).
• Gravitational Force: Calculation of the gravitational force on the satellite (F = 492 N).
• Energy Changes during orbit transfer: Changes in PE, KE and TE as satellite transitions to a lower orbit, ΔPE = -2.95x107 J, ΔKE = 1.47x107 J, ΔTE = -1.48x107 J.
• Visualizations: The simulation incorporates visual graphs that explain energy transformations in the satellite’s motion, making the concepts more accessible and understandable. The changes in KE, PE and TE are explicitly explained according to the behavior of the simulated satellite during the simulation.

3. Simulation Details and Functionality

• Interactive Elements: The simulation allows users to “fire backward thrusters” to reduce the satellite’s speed, causing it to decay to a lower orbit. Users can also fire “circular motion thrusters” to stabilize the satellite in a new, lower circular orbit, giving practical understanding of orbital adjustment..
• Model Source: The simulation uses JavaScript and HTML5 and can be embedded on any webpage using an iframe:
• <iframe width="100%" height="100%" src="https://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejss_model_gravity08_2/gravity08_2_Simulation.xhtml " frameborder="0"></iframe>
• Accessibility: The simulation is available as a HTML5 applet, making it accessible on various devices, which the website highlights with labels like: "Android/iOS including handphones/Tablets/iPads", "Windows/MacOSX/Linux including Laptops/Desktops", "ChromeBook Laptops".
• Related Resources: The webpage also lists other related resources, such as simulations by Todd Timberlake, and links to others on platforms such as scratch.mit.edu, and geogebra.org which may offer alternative perspectives or similar explorations in the subject matter of orbital mechanics.

4. Educational Value and Usage

• Conceptual Understanding: The simulation is intended to help students develop an intuitive understanding of how gravity and motion interact to create orbital paths.
• Problem Solving: The numerical examples allow the students to practice calculation of energy and forces in the context of orbital mechanics.
• Visual Learning: The graphical representation of KE, PE and TE over time is particularly useful for understanding the energy transformations taking place during orbit changes.
• Hands-on Exploration: The interactive nature of the simulation encourages students to experiment and discover concepts, leading to a more active learning experience.

5. Equations of the Simulation:

The documentation also references the specific equations used in the model, giving deeper insight for calculation and comparison of theoretical values with the simulation output:

• Kinetic Energy: “K E = G m M 2 r = 6.67 x 1 0 -11 ( 200 ) ( 6.0 x 1 0 24 ) 2 r = 8 x 1 0 16 2 * r”
• Potential Energy: "U = -m G M r = mϕ"
• Total Energy: "T E = - G m M 2 r = - 6.67 x 1 0 -11 ( 200 ) ( 6.0 x 1 0 24 ) 2 r = - 8 x 1 0 16 2 * r"

6. Credits and License:

The simulation is credited to Todd Timberlake, with a remixed version by lookang (This email address is being protected from spambots. You need JavaScript enabled to view it.); lookang; fu-kwun hwang. The content is licensed under a Creative Commons Attribution-Share Alike 4.0 Singapore License. The EasyJavaScriptSimulations Library is for commercial use under separate license, at https://www.um.es/fem/EjsWiki/Main/EJSLicense.

7. Conclusion

The "Newton's Mountain and Escape Velocity JavaScript HTML5 Applet Simulation Model" is a valuable educational resource for teaching fundamental concepts of orbital mechanics and energy transformations in a visually engaging and interactive way. The model provides detailed calculations and equations for the numerical aspects of the simulation and is accessible across multiple platforms making it an ideal addition to a physics curriculum. The simulation allows students to actively explore and discover the intricacies of satellite motion and related physics principles.

Newton's Mountain and Escape Velocity Study Guide

Quiz

Instructions: Answer each question in 2-3 sentences.

1. What is the initial launch speed required for the satellite to achieve a stable circular orbit at a distance of 2 Earth radii from the Earth's center, according to the example calculation?
2. In the initial circular orbit, what are the potential, kinetic, and total energies of the satellite, according to the example provided?
3. What is the gravitational potential at a distance of 2 Earth radii from the center of the Earth, according to the example provided?
4. Describe the direction and magnitude of the gravitational acceleration acting on the satellite in the initial circular orbit, according to the example provided.
5. What happens when the satellite fires its thrusters backward?
6. After the thrusters are fired and the orbit is lowered, what are the new values of the potential, kinetic, and total energies of the satellite, according to the example provided?
7. Calculate the change in potential energy (ΔPE) of the satellite during the transition from the initial to the lower orbit, according to the example calculation.
8. Calculate the change in kinetic energy (ΔKE) of the satellite during the transition from the initial to the lower orbit, according to the example calculation.
9. What is the significance of the first section (labeled "1") of the kinetic energy (KE) graph in the simulation provided in the source?
10. Explain how the potential energy (PE) graph changes as the satellite transitions to a lower orbit, as provided in the source.

Quiz Answer Key

1. The initial launch speed required is 5600 m/s. This speed is necessary for the satellite to maintain its circular orbit at 2 Earth radii.
2. In the initial orbit, the satellite's potential energy is -6.27x107 J, kinetic energy is 3.14x107 J, and total energy is -3.13x107 J. The kinetic energy is half the magnitude of the potential energy.
3. The gravitational potential at this point is 3.14x105 J/kg. It reflects the energy per unit mass due to the Earth’s gravitational field at that distance.
4. The gravitational acceleration is 2.46 m/s2, directed towards the Earth's center. This acceleration is what keeps the satellite in orbit.
5. When the satellite fires its thrusters backward, it reduces its speed and begins to decay toward a lower orbit. This action decreases its kinetic energy and results in an orbital change.
6. The new potential energy is -9.22x107 J, the new kinetic energy is 4.61x107 J, and the new total energy is -4.61x107 J. The lowered orbit has lower potential energy and higher kinetic energy, with the total energy now more negative.
7. The change in potential energy (ΔPE) during the transition is -2.95x107 J. This decrease is due to the satellite moving to a lower orbit, closer to the Earth.
8. The change in kinetic energy (ΔKE) during the transition is 1.47x107 J. This increase is due to the satellite speeding up as it moves to a lower orbit.
9. The first section of the kinetic energy graph represents the firing of reverse thrusters, which initiates the decay of the satellite's orbit, resulting in a decrease in KE. This decrease corresponds with the loss of kinetic energy during the burn.
10. The potential energy graph changes according to the equation U = -mGM/r, moving from right to left. As the satellite's orbital radius decreases, its potential energy also decreases, thus becoming more negative.

Essay Questions

1. Using the concepts of kinetic, potential, and total energy, explain the energy transformations that occur when a satellite transitions from a higher to a lower orbit around the Earth, referencing the simulation and calculations provided.
2. Discuss how the use of thrusters and changes in orbital velocity affect the path of a satellite as it moves from an initially circular orbit at 2 Earth radii to a lower circular orbit, based on the simulation.
3. Analyze the significance of gravitational potential and gravitational acceleration in maintaining a satellite's circular orbit, and use the example calculations provided in the source to support your claims.
4. Explain how the graphs of kinetic, potential, and total energy, as provided in the source, illustrate the energy changes experienced by the satellite throughout its orbital transitions.
5. Describe, in detail, Newton’s mountain thought experiment, and how the applet demonstrates the concept of achieving orbit, escape velocity, and the different shapes of satellite paths (e.g., circle, ellipse, parabola, hyperbola).

Glossary of Key Terms

Escape Velocity: The minimum speed needed for an object to escape the gravitational pull of a celestial body without further propulsion.

Gravitational Acceleration: The acceleration of an object due to the force of gravity. Near the surface of Earth, this is approximately 9.8 m/s². In the applet, this acceleration changes with distance.

Gravitational Force: The force of attraction between two objects with mass. It’s directly proportional to the product of their masses and inversely proportional to the square of the distance between them.

Gravitational Potential: The potential energy per unit mass at a specific point in a gravitational field. It is a scalar quantity measured in Joules per kilogram (J/kg).

Kinetic Energy (KE): The energy possessed by an object due to its motion. It is calculated as 1/2 * mass * velocity².

Orbital Decay: The gradual decrease in the altitude of a satellite’s orbit due to atmospheric drag or other perturbing forces. The applet demonstrates a change in orbit due to intentional velocity changes.

Potential Energy (PE): The energy stored by an object due to its position within a force field, such as a gravitational field.

Total Energy (TE): The sum of an object’s kinetic and potential energies. In a conservative system, it remains constant over time. In the applet, the total energy changes as energy is added or taken away by thrusters.

Thrusters: Devices used to produce thrust by expelling a fluid, typically used for orbital maneuvering of satellites and spacecraft. In this simulation, thrusters affect the speed of the satellite.

 Video

https://notebooklm.google.com/notebook/757ecf69-d31f-4de9-acd8-8b744efd004b/audio

Versions:

1. http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejs/ejs_model_NewtonsMountainwee06.jar

Other resources

1. http://physics.weber.edu/schroeder/software/NewtonsCannon.html
2. https://scratch.mit.edu/projects/898903/  Launch Simulator by Sushiboy6
3.  https://www.geogebra.org/m/jmqytcsc by Tan Seng Kwang
4.  https://www.geogebra.org/m/va3dbqyd by Tan Seng Kwang

Timeline of Events

1. Initial Stable Orbit: A 200 kg satellite is in a stable circular orbit around Earth at a distance of 2 Earth radii (2 * REarth) from the center of the Earth.
2. Reverse Thrusters Fired: The satellite fires its reverse thrusters, decreasing its speed. This initiates a decay path toward Earth.
3. Orbital Decay: As the satellite moves closer to Earth, its potential energy decreases, while its kinetic energy increases due to the increasing speed.
4. Lower Orbit Achieved: The satellite reaches a lower orbit with a radius of approximately 8.68 x 10^6 meters.
5. Circular Motion Thrusters Fired: The satellite fires thrusters to establish a stable circular orbit at the new, lower altitude.
6. Energy Changes: There are associated changes in potential energy (PE), kinetic energy (KE), and total energy (TE) due to the satellite's transition to the lower orbit, quantified as: ΔPE = -2.95x107 J, ΔKE = 1.47x107 J, ΔTE = -1.48x107 J.
7. Simulation Usage - The simulation allows users to visualize and interact with the scenario. The simulation tracks energy changes using graphs for kinetic energy, potential energy and total energy.

Cast of Characters

• Todd Timberlake: A creator of the original simulation this remixed version is based on.
• lookang: The individual responsible for remixing the original simulation.
• fu-kwun hwang: Contributed to the simulation.
• Francisco Esquembre and Félix J. García Clemente: Supported by MOE CPDD1 to host webEJS workshop.

Frequently Asked Questions about Orbital Mechanics and Satellite Motion

1. What is the concept behind Newton's Mountain, and how does it relate to satellite orbits? Newton's Mountain is a thought experiment where a cannon on a very high mountain fires a cannonball horizontally. As the projectile's speed increases, the projectile will eventually travel so far that the curvature of the Earth will be matched by the curve of the projectile's fall. Thus, rather than hitting the ground, it falls around the earth and becomes an orbiting satellite. This illustrates how achieving the correct horizontal speed allows an object to continuously fall around a celestial body instead of crashing into it.
2. How do the potential energy (PE), kinetic energy (KE), and total energy (TE) of a satellite change as its orbit changes? When a satellite moves to a lower orbit, its potential energy (PE) decreases (becomes more negative), as it is closer to the center of the Earth's gravity. The satellite's kinetic energy (KE) increases as it needs to move faster to maintain the orbit at the lower altitude. However, the total energy (TE) of the satellite also decreases. This decrease is a result of the energy being used to change orbits. The provided example shows these changes, with a decrease in PE, an increase in KE and a decrease in TE when a satellite lowers its orbit.
3. What role do thrusters play in changing a satellite's orbit, and how does this affect the energy of the system? Thrusters are used to either increase or decrease a satellite's velocity. Firing thrusters backward (reverse thrusters) reduces the satellite's speed, causing its orbit to decay. This action decreases both its kinetic and total energy. On the other hand, once the satellite has descended to a lower altitude, circular motion thrusters can be fired to establish a new circular orbit. The key idea is that changes in the orbital path and altitude are managed through controlled changes in the satellite's speed through thrusters.
4. What is the relationship between the gravitational potential and the gravitational acceleration at a point in space? Gravitational potential (ϕ) is the potential energy per unit mass at a particular point in a gravitational field, with units of J/kg. It’s a scalar value. The gravitational acceleration (a) is the acceleration experienced by an object due to gravity at that same point and has units of m/s². The acceleration, a vector, points toward the center of the mass causing the gravitational field and is related to the gradient of the potential field. In the provided example, the gravitational potential and acceleration at a distance of 2 Earth radii are given as 3.14 x 10^5 J/kg and 2.46 m/s² toward the center of Earth respectively.
5. How does the kinetic energy of a satellite change during an orbital decay path, and what is the significance of this change? During an orbital decay path, as the satellite moves to lower altitude, its kinetic energy (KE) increases. This happens because it is trading potential energy (as it gets closer to the earth) to increase its speed. The KE increase allows the satellite to maintain a stable orbit at a lower altitude, and it’s a critical part of understanding how satellites are able to change orbital heights.
6. What does the graph of potential energy for a satellite's orbit transition tell us about its movement? The potential energy (PE) graph moves according to the equation U = -mGM/r = mϕ. As a satellite moves from a higher orbit to a lower one, the graph shows the transition from right to left, and a decrease in PE as the radius of its orbit gets smaller. This decrease happens as the satellite goes from higher potential energy (further from the earth) to lower potential energy(closer to the earth).
7. How do the graphs of kinetic energy, potential energy, and total energy relate to each other during a satellite's orbit transition? During an orbit transition, the kinetic energy and potential energy trade off with one another. If a satellite is using reverse thrusters, it loses speed, reducing kinetic energy and total energy. Then, if the satellite moves to a lower orbit, its kinetic energy will increase while its potential energy decreases. The total energy graph reflects these changes and the energy needed to change the orbit. The total energy graph will decrease when the thrusters are used. In a stable orbit, the total energy remains constant.
8. Can you explain the energy values given in the example problem for both the initial and lowered orbit? The example provides specific energy values. In the initial orbit at 2 Earth radii, the satellite has potential energy (PE) of -6.27x10^7 J, kinetic energy (KE) of 3.14x10^7 J, and a total energy (TE) of -3.13x10^7 J. After lowering the orbit, with a new radius of 8.68x10^6 m, the energies are: PE = -9.22x10^7 J, KE = 4.61x10^7 J, TE = -4.61x10^7 J. The negative values for PE and TE indicate the satellite is in a bound orbit, meaning it's held by the Earth's gravity. The change in these values demonstrates the energy transformations required to adjust the satellite's trajectory.