About

Newtonian orbits and the equivalent one-dimensional problem

This simulation solves Kepler's problem for the Newtonian potential V(r) = -k/r, mechanical energy E and angular momentum L > 0, in dimensionless variables:

• Unit mass is 2-body system's reduced mass m.
• Unit length is the position of the minimum of the effective potential energy in the attractive case (i.e., the radius of the circular orbit): r₀ = L²/m|k|.
• Time unit is L³/mk².
• In these unit we have m = L = |k| = 1, the orbit equation is 1/r = ε cos(φ-φ₀) + η with η = |k|/k. The eccentricity is ε = (1+2E)^1/2, the effective potential energy -η/r+1/2r² and its minimum is at point (1,-1/2) for attractive forces.

• If Orbit is selected, along with the orbit one can see the conserved Laplace-Runge-Lenz vector, which goes through the pericentron.
• To get information on one element, put over it the mouse pointer to see the corresponding tooltip.
  

Activities

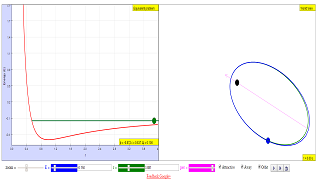
• On the left one can see the effective potential energy corresponding to the equivalent one-dimensional problem (in red).
  • Use the mouse (or the corresponding numerical entries) to change the mechanical energy E and the initial value of the polar distance r: the polar angle φ (phi in the simulation) will be set automatically.
  • Discuss the values of the eccentricity ε (e) and the form of the orbit for different values of E.
  • Uncheck Attracting and discuss what happens with repulsive forces.
  • Change orbit's spatial orientation by choosing the pericentron position φ₀ (called per in the simulation) or use the following procedure.
• The plane relative motion is displayed on the right. Use the mouse to select the initial position and the orbit orientation.
• With the simultaneous evolutions in the double display you can check that the return points of the one-dimensional problem correspond in the full problem to apses, where the velocity does not vanish, but is perpendicular to the radius.

This is an English translation of the Basque original for a course on mechanics, oscillations and waves.
It requires Java 1.5 or newer and was created by Juan M. Aguirregabiria with Easy Java Simulations (Ejs) by Francisco Esquembre. I thank Wolfgang Christian and Francisco Esquembre for their help.  

Translations

Code	Language		Translator	Run

Credits

Juan M. Aguirregabiria (http://tp.lc.ehu.es/jma.html); lookang; tina

http://iwant2study.org/lookangejss/02_newtonianmechanics_7gravity/ejss_model_keplerwee1/keplerwee1_Simulation.xhtml

Briefing Document: 🪐 Kepler Orbit JavaScript Simulation

1. Overview

This document reviews the "Kepler Orbit JavaScript HTML5 Applet Simulation Model" resource, part of the Open Educational Resources / Open Source Physics @ Singapore collection. The simulation is designed to help students understand Newtonian orbits, particularly in the context of gravitational forces and Kepler's problem. It allows users to manipulate parameters and visualize the resulting orbital motion and related physical concepts. The resource is described as being a translation of an original Basque version, designed for a course on mechanics, oscillations, and waves.

2. Main Themes and Concepts

• Newtonian Orbits and Kepler's Problem: The simulation directly addresses Kepler's problem within the framework of Newtonian mechanics. It models the motion of a body under the influence of a Newtonian potential (specifically, the attractive or repulsive inverse-square law force). The core problem being solved is based on the equation V(r) = -k/r, where V is the potential and r the distance.
• Effective One-Dimensional Problem: The simulation simplifies the two-dimensional orbital motion into an equivalent one-dimensional problem, which is represented by an effective potential energy curve. This allows users to explore orbital characteristics and turning points in a simplified manner. The effective potential energy is described as - η / r +1/2 r 2 .
• Conserved Quantities: The simulation highlights the conservation of mechanical energy (E) and angular momentum (L). It also visualizes the Laplace-Runge-Lenz vector, which is a conserved quantity in the Kepler problem and points towards the pericentron of the orbit.
• Dimensionless Variables: The simulation uses dimensionless variables, which simplifies the equations and allows for a more generalized treatment of the problem. The units are chosen such that m = L = | k | = 1, unit length is the radius of a circular orbit r 0 = L 2/ m | k | , and unit time is L 3/ mk 2. These choices allow for a cleaner and more general representation of the system.
• Eccentricity: The simulation allows users to explore the relationship between mechanical energy and the eccentricity of the orbit: ε = (1+2 E )1/2. This is a key feature in understanding the different types of orbits (elliptical, parabolic, hyperbolic).
• Attractive vs. Repulsive Forces: Users can switch between attractive and repulsive forces. This demonstrates the change in the behavior of the system. Switching from 'Attracting' to not attracting gives the repulsive form of the orbit.
• Pericenter Position: The simulation allows the user to manipulate the orbit’s spatial orientation by adjusting the pericentron position, also called φ 0 (called per in the simulation). This is another way to investigate the geometry of the orbit.

3. Key Ideas and Facts

• Simulation's Equation: The orbit equation is given as 1/ r = ε cos( φ - φ 0) + η with η = | k |/ k. This is the mathematical core of the simulation that produces the orbital shapes.
• Laplace-Runge-Lenz Vector: The visualization of this vector going through the pericentron is crucial in understanding the conserved quantities in the Kepler problem.
• Apses: The simulation connects the one-dimensional effective potential problem to the full two-dimensional problem, showing that "the return points of the one-dimensional problem correspond in the full problem to apses." Apses are points where the velocity is perpendicular to the radius.
• Interaction: The simulation is interactive. The user can, "use the mouse (or the corresponding numerical entries) to change the mechanical energy E and the initial value of the polar distance r" as well as changing the pericentron position using "the mouse to select the initial position and the orbit orientation".
• Visualizations: "With the simultaneous evolutions in the double display you can check that the return points of the one-dimensional problem correspond in the full problem to apses, where the velocity does not vanish, but is perpendicular to the radius."

4. Learning Goals (as stated in the document)

The listed learning goals for students using this simulation are extensive and indicate a thorough approach to understanding gravity and orbits, including:

• Understanding gravitational fields and forces.
• Recognizing analogies between gravitational and electric fields.
• Applying Newton's law of gravitation: ( |F| = \frac{GM_{1}M_{2}}{r^{2}} )
• Deriving the equation for gravitational field strength of a point mass: g=GMr2
• Applying the equation g=GMr2
• Understanding that g is approximately constant near the Earth's surface.
• Defining gravitational potential and its equation ( \phi = -\frac{GM}{r} ).
• Analyzing circular orbits in inverse square law fields.
• Understanding geostationary orbits.

5. Target Audience

Based on the learning goals, this simulation is primarily intended for:

• High school and introductory university physics students studying Newtonian mechanics and gravitation.
• Students learning about orbital motion and Kepler's laws.
• Students learning about the mathematical descriptions of gravitational fields and related quantities.

6. Technical Details

• Technology: The simulation is an HTML5 applet, built using Easy Java Simulations (Ejs). This allows it to run in a web browser, requiring no additional software.
• Credits: The original model was created by Juan M. Aguirregabiria with Easy Java Simulations (Ejs) by Francisco Esquembre. It was translated into English by lookang and tina.
• Access: The simulation can be embedded in a webpage using an <iframe> tag, making it easy to integrate into educational resources.

7. Additional Resources

• The webpage lists a plethora of other simulation models that relate to physics and mathematics. These models could complement and enrich the learning experience with the Kepler model.

8. Conclusion

The Kepler Orbit JavaScript HTML5 Applet Simulation Model is a valuable resource for teaching Newtonian mechanics and gravitational orbits. Its interactive nature, coupled with its clear visualization of physical concepts and mathematics, makes it well-suited for educational use. The model provides a platform for exploring topics such as conserved quantities, eccentricity, repulsive and attractive forces, and spatial orientation and should be beneficial for students learning about these concepts.

 

Kepler Orbit Simulation Study Guide

Quiz

Instructions: Answer the following questions in 2-3 sentences each.

1. What problem does the Kepler Orbit simulation model solve?
2. What are the three dimensionless variables used in the simulation?
3. What does the simulation's "effective potential energy" graph represent?
4. What is the significance of the pericentron in the orbit?
5. How can users alter the orbit's spatial orientation in the simulation?
6. According to the text, how does the one-dimensional problem relate to the full problem?
7. What is the purpose of the Laplace-Runge-Lenz vector in the orbit display?
8. What happens to the orbit when the "Attracting" option is unchecked?
9. What is the relationship between the mechanical energy E and eccentricity ε?
10. What are apses in relation to the simulation and the velocity?

Quiz Answer Key

1. The simulation solves Kepler's problem for the Newtonian potential, focusing on the relationship between potential energy, mechanical energy, and angular momentum in a two-body system, displaying orbital motion. It’s based on a simplified model using dimensionless units.
2. The three dimensionless variables are unit mass (reduced mass m of the 2-body system), unit length (radius of circular orbit r₀), and unit time (related to angular momentum, mass, and gravitational constant). The values of the units are m = L = |k| = 1 in this dimensionless system.
3. The effective potential energy graph, shown in red on the left side of the simulation, represents the potential energy experienced by the orbiting object as a function of its distance from the central body, incorporating both the gravitational potential and the effect of angular momentum.
4. The pericentron is the point in the orbit where the orbiting object is closest to the central body. The Laplace-Runge-Lenz vector always points towards the pericentron, indicating the orbit's orientation and direction of the closest approach.
5. Users can alter the orbit's spatial orientation by either changing the pericentron position (φ₀), called "per" in the simulation, or by selecting the initial position and orientation directly in the plane of relative motion display.
6. The return points in the one-dimensional effective potential energy problem correspond to the apses (points of closest and furthest approach) in the full two-dimensional orbital problem. At these points, the velocity vector of the orbiting body is perpendicular to the radius.
7. The Laplace-Runge-Lenz vector, displayed when the "Orbit" box is checked, is a conserved quantity that always points to the pericentron, visually indicating the direction of closest approach within the orbit.
8. Unchecking "Attracting" changes the force to a repulsive one, leading to a hyperbolic orbit where the objects move away from each other rather than orbiting in a closed path. The potential changes to positive.
9. The eccentricity ε is defined as ε = (1 + 2E)1/2, and depends entirely on the mechanical energy E. Changes to mechanical energy lead to different orbit shapes (e.g., circular, elliptical, parabolic, hyperbolic).
10. Apses are the points in an orbit where the radial velocity of the orbiting body is zero. They represent either the closest (pericenter) or furthest (apocenter) approach to the central body, where velocity is perpendicular to the radius vector.

Essay Questions

Instructions: Answer the following questions in essay format, referencing the provided source material.

1. Discuss how the Kepler Orbit simulation simplifies the analysis of orbital motion by using dimensionless variables and reduced mass. What are the advantages of this approach?
2. Explain the role of the effective potential energy in understanding the different types of orbits (circular, elliptical, hyperbolic) demonstrated in the simulation.
3. Analyze the relationship between mechanical energy, eccentricity, and the overall shape of an orbit. Use examples from the simulation to illustrate your points.
4. Describe how the Laplace-Runge-Lenz vector provides insight into the characteristics of an orbit and how it’s conserved in the simulation.
5. Compare and contrast the orbital behaviors observed when the gravitational force is attractive versus repulsive, explaining the underlying physics principles at play.

Glossary of Key Terms

Apses: Points in an orbit where the radial velocity of the orbiting object is zero. Specifically, these are the pericenter (closest approach) and apocenter (furthest approach).

Dimensionless Variables: Quantities that do not have physical units, often used to simplify equations and analysis by scaling away specific physical units. In this simulation, unit mass, length, and time are set to 1.

Eccentricity (ε): A measure of how much an orbit deviates from a perfect circle. In this context, ε = (1+2E)1/2 where E is the mechanical energy.

Effective Potential Energy: The sum of the gravitational potential energy and a term related to angular momentum, used to analyze orbital motion as an equivalent one-dimensional problem.

Kepler's Problem: The problem of determining the orbit of a planet or other body moving under the gravitational influence of another massive body.

Laplace-Runge-Lenz Vector: A conserved quantity in Keplerian motion that points towards the pericenter, indicating the direction of the closest approach and providing information about the orientation of the orbit.

Mechanical Energy (E): The sum of the kinetic and potential energies of the orbiting object. In the context of Kepler's problem, the mechanical energy determines the type of orbit.

Newtonian Potential: The gravitational potential energy of a system of masses according to Newton's law of universal gravitation. In this context, it is V(r) = - k/ r, where k is a constant related to the gravitational force and r is distance.

Pericenter/Pericentron: The point in an orbit where the orbiting object is closest to the central body.

Reduced Mass (m): A simplified representation of the masses in a two-body system, used to reduce the problem to a one-body system.

Sample Learning Goals

Students should be able to:

1. show an understanding of the concept of a gravitational field as an example of field of force and define the gravitational field strength at a point as the gravitational force exerted per unit mass placed at that point.
2. recognise the analogy between certain qualitative and quantitative aspects of gravitational and electric fields.
3. recall and use Newton’s law of gravitation in the form \( |F| = \frac{GM_{1}M_{2}}{r^{2}} \) 
4. derive, from Newton’s law of gravitation and the definition of gravitational field strength, the equation g=GMr2for the gravitational field strength of a point mass.
5. recall and apply the equation g=GMr2 for the gravitational field strength of a point mass to new situations or to solve related problems.
6. show an understanding that near the surface of the Earth g is approximately constant and equal to the acceleration of free fall.
7. define the gravitational potential at a point as the work done per unit mass in bringing a small test mass from infinity to that point.
8. solve problems using the equationϕ=-GMrfor the gravitational potential in the field of a point mass.
9. analyse circular orbits in inverse square law fields by relating the gravitational force to the centripetal acceleration it causes.
10. show an understanding of geostationary orbits and their application.

For Teachers

Video

[text]

 Version:

Other Resources

1. https://www.geogebra.org/m/FW8SkHWh by ukukuku

FAQ: Kepler Orbit Simulation

• What does the Kepler Orbit JavaScript HTML5 Applet Simulation Model demonstrate? This simulation visualizes the motion of a body under the influence of a Newtonian potential, specifically the V ( r ) = - k / r potential, which represents an attractive force like gravity. It allows users to explore how parameters such as mechanical energy (E) and angular momentum (L) affect the shape of the orbit (elliptical, circular, hyperbolic) and provides a visual representation of these orbits. It also lets users examine the effect of repulsive forces.
• What is the "effective potential energy" shown in the simulation? The "effective potential energy" is a concept used to simplify the two-dimensional orbital problem into an equivalent one-dimensional problem. It combines the actual potential energy (e.g., gravitational potential) with a term representing the centrifugal effect due to angular momentum. This effective potential helps visualize the possible radial motion of the orbiting body. Specifically, the simulation visualizes the effective potential energy as - η / r +1/2 r 2.
• What are the key variables and parameters that can be adjusted in the simulation? Users can adjust the mechanical energy (E) and initial polar distance (r) of the orbiting body through mouse interaction or numerical input. The initial polar angle (φ) is set automatically based on these. Users can also control the initial orbital orientation using the pericentron position (φ0 or "per") and also choose whether to use an attractive or repulsive force. The simulation also dynamically displays the eccentricity (ε) of the orbit.
• What is the significance of the Laplace-Runge-Lenz vector shown in the simulation? The Laplace-Runge-Lenz vector is a conserved quantity in the Kepler problem, meaning it remains constant during the motion. The simulation shows that this vector points towards the pericentron (the point of closest approach in the orbit). It's a characteristic feature of orbits under a 1/r potential, which the simulation is based on.
• How does the simulation explain the concepts of apses and velocities in orbital motion? The simulation displays two views: the equivalent one-dimensional problem using the effective potential energy on the left, and the full two-dimensional plane relative motion on the right. Apses (points of closest and farthest approach) in the full orbit are shown to correspond to the return points in the one-dimensional problem where the velocity along the radius is zero. The simulation also clarifies that at apses the velocity is not zero, but it is perpendicular to the radius.
• What is the unit of mass, length and time used in the simulation? The simulation employs dimensionless units to simplify calculations: the unit mass is the reduced mass of the two-body system, length is the radius of a circular orbit, and the time unit is related to the angular momentum, mass, and force constant. In these units, the mass, angular momentum and force constant absolute value have a value of 1 (m = L = | k | = 1).
• What are some practical learning goals associated with understanding the simulation? The simulation enables students to understand gravitational fields and their strengths, recognizing parallels between gravitational and electric fields. They are intended to apply Newton’s law of gravitation and understand how it translates to the strength of a gravitational field of a point mass. It aims to help students derive the equation for the gravitational field of a point mass and apply it to problems. It also covers how gravity relates to the constant acceleration near Earth's surface and what gravitational potential means and how it relates to work per unit mass. Finally it explains how gravitational force translates into centripetal acceleration and how that relates to understanding circular and geostationary orbits.
• Is this just a single simulation, or part of a larger resource? This simulation is part of a larger collection of open educational resources focused on physics. The page contains links to other simulations including: gravity models, electromagnetic field lines, oscillations, wave properties, thermodynamics and other concepts, created with Easy Java Simulations (Ejs). There are also many modeling using Tracker video analysis software also. This suggests the simulation is not an isolated entity but rather a part of a more complete interactive curriculum.